1) Dla jakich wartości parametru m, suma oraz iloczyn pierwiastków równania:
2(x² - 1) - m (x + 1) + x = 0 są liczbami tego samego znaku?
ODPOWIEDŹ: dla m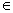 
(-2;1)
2) a) Dla jakich wartości x wielomian W(x) = x³ + bx² + cx + d , przyjmuje wartości dodatnie, jeżeli
W(-1)=6; W(-2)=8;
W(2)=0 ?
ODPOWIEDŹ: dla x 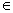(-3; 0) 
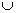(2; +∞); b = 1; c = - 6; d = 0;
b*) Wykaż, że jeżeli liczby rzeczywiste x1, x2, x3 są pierwiastkami wielomianu:
W(x) = x³ + px + q, to: x1² + x2² + x3² = - 2p i x1³ + x2³ + x3³=-3q - zadanie na szóstkę.
3) W ciągu arytmetycznym (an) dane są wyrazy: a1 = log2x; a2 = log2 (x + 6); a3 = log2 (x + 60).
W ciągu geometrycznym (bn) y - 2 y² - 3 y dane są wyrazy: b1 = 2 ; b2 = 2 ; b3 = 2 ;
Suma 10 początkowych wyrazów ciągu (bn) jest większa od sumy 31 początkowych wyrazów ciągu (an).
Znajdź x i y.
ODPOWIEDŹ: x = 2; y = 2;
4) Bok prostokąta ma długość 60 cm. O ile musi być dłuższy od niego drugi bok, aby po wyjęciu z tego prostokąta otworu kołowego o średnicy równej różnicy długości boków tego prostokąta, pozostała część miała największe pole powierzchni? Oblicz to pole.
ODPOWIEDŹ: drugi bok musi być dłuższy o: 120/π; pole otrzymanej figury: P= -¼ π x² + 60x + 3600;
pole figury o największej powierzchni: fmax(120/π )= (3600/π) • (1+π);
5) Dane są równania prostych, zawierających boki trójkąta: x - 2 = 0; x - 2y - 2 = 0 oraz 2x + y - 9 = 0. Trójkąt ten obraca się dookoła, w której zawiera się najdłuższy jego bok. Oblicz objętość i pole powierzchni otrzymanej bryły.
ODPOWIEDŹ: objętość: V= (20/3)π [j³]; pole: P=6π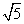
[j²];
