Asymptota ukośna funkcji f to prosta A(x) o równaniu A(x)=ax+b o tej własności, że odległość między wartością funkcji f w punkcie x a wartością asymptoty w tym samym punkcie dąży do zera w plus lub minus nieskończoności, czyli gdy 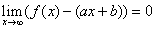 lub gdy
lub gdy 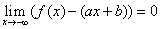 .
.
W pierwszym przypadku mamy do czynienia z asymptotą prawostronną, w drugim – z lewostronną. Jeśli asymptota jest jednocześnie lewostronna i prawostronna, to nazywa się ją obustronną.
Aby wyliczyć asymptotę ukośną należy:
- policzyć granicę funkcji
![]() w plus lub minus nieskończoności – zależnie od tego, czy liczymy asymptotę prawo- czy lewostronną. Oznaczmy wartość granicy jako a.
w plus lub minus nieskończoności – zależnie od tego, czy liczymy asymptotę prawo- czy lewostronną. Oznaczmy wartość granicy jako a. - policzyć granicę funkcji
![]() w plus lub minus nieskończoności, zależnie od tego czy liczymy prawostronną czy lewostronną. Oznaczmy wartość tej granicy jako b.
w plus lub minus nieskończoności, zależnie od tego czy liczymy prawostronną czy lewostronną. Oznaczmy wartość tej granicy jako b. - Jeśli obie te granice istnieją, to asymptota jest prostą o równaniu A(x)=ax+b. Jeśli przynajmniej jedna z tych granic nie istnieje lub jest granicą niewłaściwą, to asymptota nie istnieje.

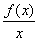 w plus lub minus nieskończoności – zależnie od tego, czy liczymy asymptotę prawo- czy lewostronną. Oznaczmy wartość granicy jako a.
w plus lub minus nieskończoności – zależnie od tego, czy liczymy asymptotę prawo- czy lewostronną. Oznaczmy wartość granicy jako a.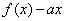 w plus lub minus nieskończoności, zależnie od tego czy liczymy prawostronną czy lewostronną. Oznaczmy wartość tej granicy jako b.
w plus lub minus nieskończoności, zależnie od tego czy liczymy prawostronną czy lewostronną. Oznaczmy wartość tej granicy jako b.
