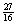Badanie przebiegu zmienności funkcji to postępowanie dzięki któremu możemy dowiedzieć się o podstawowych własnościach funkcji koniecznych do tego, by narysować jej wykres.
Ogólny schemat przebiegu zmienności funkcji podany jest poniżej.
1. Analiza funkcji
a. wyznaczenie dziedziny funkcji
b. wyznaczenie przedziałów ciągłości funkcji
c. wyznaczenie granic na końcach tych przedziałów
d. wyznaczenie przedziałów różniczkowalności funkcji
e. sprawdzenie parzystości/nieparzystości/okresowości
f. można znajdować też punkty przecięcia wykresu funkcji z osiami układu współrzędnych - w szczególności miejsca zerowe funkcji, czyli punkty przecięcia z osią X
2. Analiza pierwszej pochodnej funkcji, w tym znajdowanie miejsc zerowych pierwszej pochodnej, ekstremów funkcji oraz przedziałów monotoniczności funkcji
3. Analiza drugiej pochodnej, w tym znajdowanie punktów przegięcia funkcji, przedziałów wypukłości i wklęsłości funkcji
4. Wyznaczenie asymptot, o ile istnieją
5. Narysowanie tabeli przebiegu funkcji
6. Sporzędzenie wykresu funkcji i wyznaczenie zbioru wartości funkcji
PRZYKŁAD
Zbadamy przebieg zmienności funkcji 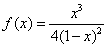 .
.
Wyznaczenie dziedziny. Dziedziną jest zbiór 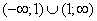 - dla x=1 mianownik się zeruje.
- dla x=1 mianownik się zeruje.
Przedziały ciągłości. Funkcja jest ciągła w przedziałach 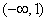 oraz
oraz 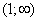 . W przedziałach tych funkcja posiada pochodne dowolnego rzędu.
. W przedziałach tych funkcja posiada pochodne dowolnego rzędu.
Granice na końcach przedziałów.
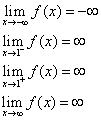
Aysmptota pionowa. Prosta x=1
Asymptota ukośna obustronna. 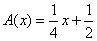
Miejsce zerowe funkcji. Widać, że jedyne miejsce zerowe to x=0. Funkcja przechodzi więc przez początek układu współrzędnych.
Zauważmy, że nie ma sensu badać parzystości, gdyż przedziały, na których funkcja jest określona, nie są rozmieszczone symetrycznie względem zera.
Pierwsza pochodna. 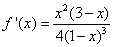
Miejsca zerowe pierwszej pochodnej to 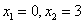 .
.
Pochodna jest dodatnia w przedziałach 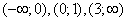 , ujemna w przedziale
, ujemna w przedziale 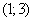 . Zatem funkcja jest rosnąca w każdym z pierwszych trzech przedziałów, a malejąca w przedziale (1;3).
. Zatem funkcja jest rosnąca w każdym z pierwszych trzech przedziałów, a malejąca w przedziale (1;3).
W punkcie x=0 funkcja nie ma extremum, gdyż pochodna w tym punkcie nie zmienia znaku. W punkcie x=3 funkcja ma ekstremum lokalne równe 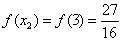 .
.
Druga pochodna. 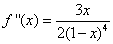 .
.
Druga pochodna zeruje się tylko w punkcie x=0. Druga pochodna jest ujemna w przedziale 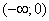 , a dodatnia w przedziałach
, a dodatnia w przedziałach 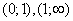 , zatem w pierwszym przedziale funkcja jest wklęsła, a w dwóch ostatnich - wypukła. Ponieważ druga pochodna zeruje się w x=0, zatem punkt (0,f(0))=(0,0) jest punktem przegięcia funkcji.
, zatem w pierwszym przedziale funkcja jest wklęsła, a w dwóch ostatnich - wypukła. Ponieważ druga pochodna zeruje się w x=0, zatem punkt (0,f(0))=(0,0) jest punktem przegięcia funkcji.
Tabela zmienności funkcji:
|
x
|
(-∞;0)
|
0
|
(0;1)
|
1
|
(1;3)
|
3
|
(3,∞)
|
|
f'
|
+
|
0
|
+
|
brak
|
-
|
0
|
+
|
|
f''
|
-
|
0
|
+
|
brak
|
+
|
+
|
+
|
|
f
|
-∞
|
0
p.przeg.
|
|
brak
|
∞
|
minimum
|
|
|
kształt strzałek pokazuje nie tylko monotoniczność, ale także wklęsłość lub wypukłość
| |||||||

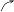
 ∞
∞