1. Zbiory. Działania na zbiorach.
Zbiór oraz element zbioru to pojęcia pierwotne.
jeśli x jest elementem zbioru A to xÎA, x należy do zbioru A
jeśli y nie jest elementem zbioru A to yÏA, y nie należy do zbioru A
Każdy zbiór wyznaczony jest jednoznacznie przez jego elementy.
Zbiór skończony – zbiór, który ma skończoną liczbę elementów.
Zbiór pusty - Æ – zbiór, który nie ma należących do niego elementów.
Zbiór nieskończony – zbiór, który nie jest ani skończony, ani pusty.
Równość zbiorów:
A = B Û (dla każdego x : xÎA Û xÎB )
Zawieranie się zbiorów, podzbiory:
A Ì B Û ( dla każdego x: xÎA Þ xÎB )
Zbiory rozłączne – zbiory, które nie mają ani jednego elementu wspólnego.
Suma zbiorów A È B:
xÎA È B Û ( xÎA lub xÎB )
Iloczyn zbiorów A Ç B:
xÎA Ç B Û ( xÎA i xÎB )
Różnica zbiorów A B:
xÎA B Û ( xÎA i xÏB )
Dopełnienie zbioru A ( symbol A’ ):
Jeśli wszystkie zbiory znajdują się w ustalonym zbiorze X, nazywanym przestrzenią, to dopełnieniem naszego zbioru A będzie różnica X A
Symbolicznie:
X -przestrzeń i A Ì X, to A’ = X A
Iloczyn kartezjański ( produkt ) zbiorów A ´ B:
Iloczyn kartezjański to uporządkowana para liczb (x,y), w której element x należy do zbioru A, a element y należy do zbioru B.
Symbolicznie:
( x, y )ÎA´B Û ( xÎA i yÎB )
Niektóre prawa rachunku zbiorów:
|
nazwa prawa
|
treść prawa
|
|
przemienność dodawania
|
A È B = B È A
|
|
przemienność iloczynu
|
A Ç B = B Ç A
|
|
łączność dodawania
|
(A È B) È C = A È (B È C)
|
|
łączność iloczynu
|
(A Ç B) Ç C = A Ç (B Ç C)
|
|
rozdzielność mnożenia względem dodawania
|
(A È B) Ç C =(A Ç C) È (B Ç C)
|
|
rozdzielność dodawania względem mnożenia
|
(A Ç B) È C =(A È C) Ç (B È C)
|
|
prawa
de’Morgana
|
(A Ç B)’ = A’ È B’
(A È B)’ = A’ Ç B’
|
2. Układy równań i nierówności.
Wartość bezwzględna dla liczby rzeczywistej
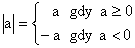
Nierówności z wartością bezwzględną
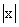 < a , to xÎ( -a, a )
< a , to xÎ( -a, a ) 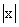 > a , to xÎ( -¥, -a ) È ( a, ¥ )
> a , to xÎ( -¥, -a ) È ( a, ¥ )
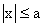 , to xÎ[ -a, a ]
, to xÎ[ -a, a ] 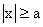 , to xÎ( -¥, -a ] È [ a, ¥ )
, to xÎ( -¥, -a ] È [ a, ¥ )
Rozwiązywanie układów równań liniowych
Rozwiązaniem układu równań liniowych ( stopnia pierwszego ) z dwiema niewiadomymi jest każda para liczb, która spełnia jednocześnie pierwsze i drugie równanie.
Mamy układ równań 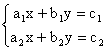 (*)
(*)
Wyznacznikami układu są liczby:
W = 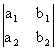 = a1 × b2 - a2 × b1;
= a1 × b2 - a2 × b1;
Wx = 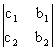 = c1 × b2 - c2 × b1;
= c1 × b2 - c2 × b1;
Wy = 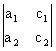 = a1 × c2 - a2 × c1;
= a1 × c2 - a2 × c1;
Układ równań (*) jest układem równań:
- niezależnych Û W ¹ 0, wtedy układ ma dokładnie jedno rozwiązanie dane wzorami:
x = 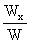 , y =
, y =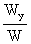 ,
,
interpretacja geometryczna układu to dwie proste, które się przecinają
- zależnych Û W = 0 i Wx = 0 i Wy = 0, wtedy układ ma nieskończenie wiele rozwiązań ( x, y ) takich, że x Î R, a y = -
![]() x +
x + ![]() ;
;
interpretacja geometryczna układu to dwie proste, które się pokrywają
c. sprzecznych Û W = 0 i Wx ¹ 0 lub Wy ¹ 0, zbiór rozwiązań układu to zbiór pusty,
interpretacja geometryczna układu to dwie proste, które się równoległe.
3. Funkcja kwadratowa.
Funkcja kwadratowa (trójmian kwadratowy) to funkcja f określona wzorem postaci
f(x) =ax2 + bx + c,
gdzie a, b, c Î R i a ¹ 0.
Postać kanoniczna trójmianu kwadratowego to postać:
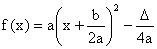 ,
,
gdzie D =b2-4ac. D nazywamy wyróżnikiem trójmianu kwadratowego.
Miejsca zerowe funkcji kwadratowej:
- funkcja kwadratowa ma dwa różne miejsca zerowe x1, x2 wtedy i tylko wtedy, gdy D>0,
tymi miejscami zerowymi są: 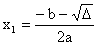 ,
, 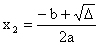 ,
,
- funkcja kwadratowa ma dokładnie jedno miejsce zerowe x1 wtedy i tylko wtedy, gdy D=0,
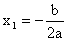 ,
,
- funkcja kwadratowa nie ma miejsc zerowych wtedy i tylko wtedy, gdy D<0.
Iloczynowa postać funkcji kwadratowej:
- jeżeli D>0, wtedy trójmian kwadratowy y = ax2 + bx + c (gdzie a ¹ 0) można zaprezentować w postaci iloczynu y = a(x-x1)(x-x2),
gdzie x1, x2 są to miejsca zerowe trójmianu kwadratowego;
- jeżeli D=0, to trójmian kwadratowy y= ax2 + bx + c (a ¹ 0) można przedstawić w postaci iloczynu y = a(x-x1)2, gdzie x1 jest miejscem zerowym trójmianu kwadratowego.
Wzory Viete’a
Jeżeli trójmian kwadratowy y= ax2 + bx + c (a ¹ 0) ma miejsce zerowe (dwa lub jedno) x1, x2, to
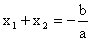 ,
,
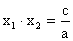 .
.
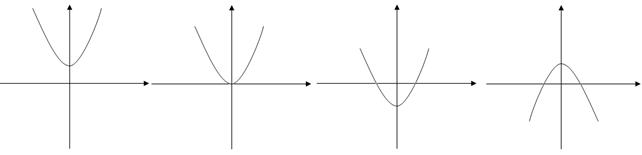
Wykres funkcji kwadratowej y= ax2 + bx + c, gdzie a ¹ 0, jest krzywą - parabolą. Wierzchołek paraboli ma współrzędne: 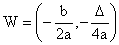 .
.
Dla a < 0 w wierzchołku paraboli mamy maksimum funkcji kwadratowej,
Dla a > 0 w wierzchołku paraboli mamy minimum funkcji kwadratowej.
a > 0 a >0 a > 0 a < 0
D < 0 D = 0 D > 0 D > 0
4. Wielomiany
Wielomianem stopnia n jednej zmiennej nazywamy funkcję W: R ® R postaci:
W(x)=a0 + a1x + a2x2 + ... + anxn,
gdzie a0, a1, a2, ..., an Î R i an ¹ 0, n Î N.
Liczby a0, a1, a2, ..., an nazywamy współczynnikami wielomianu W.
Dwa wielomiany są równe wtedy i tylko wtedy, gdy są tego samego stopnia i mają równe współczynniki przy odpowiednich potęgach zmiennej.
Wielomian W jest podzielny przez wielomian W1 jeśli istnieje wielomian Q taki, że
W(x) = W1(x)×Q(x) dla każdego x Î R.
Dla każdej pary wielomianów W i W1 takich, że stopień wielomianu W1 jest dodatni, istnieje dokładnie jeden układ wielomianów Q i R, dla których W(x)=W1(x)×Q(x)+R(x) (dla każdego
x Î R) i stopień wielomianu R jest mniejszy od stopnia wielomianu W1 lub wielomian R jest zerowy. Wielomian R nazywamy resztą z dzielenia wielomianu W przez wielomian W1.
Reszta z dzielenia wielomianu W przez dwumian postaci ( x – r ), gdzie r Î R, jest równa liczbie W(r).
Twierdzenie Bézouta. Liczba a jest pierwiastkiem wielomianu W wtedy i tylko wtedy, gdy wielomian W jest podzielny przez dwumian ( x –a ).
Jeżeli liczba wymierna 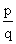 jest miejscem zerowym wielomianu W(x)=a0+a1x+a2x2+...+anxn, gdzie an¹0, to q jest dzielnikiem współczynnika an, zaś p jest dzielnikiem współczynnika a0.
jest miejscem zerowym wielomianu W(x)=a0+a1x+a2x2+...+anxn, gdzie an¹0, to q jest dzielnikiem współczynnika an, zaś p jest dzielnikiem współczynnika a0.
5. Funkcja wykładnicza i logarytmiczna
Funkcją wykładniczą jednej zmiennej nazywamy funkcję f: ( R ) ® R+ określoną wzorem postaci:
f ( x ) = ax, gdzie aÎR+ .
Własności funkcji wymiernej:
- Funkcja f ( x ) = ax przyjmuje tylko wartości dodatnie;
- Funkcja f ( x ) = ax jest rosnąca gdy a > 1;
- Funkcja f ( x ) = ax jest stała gdy a = 1;
- Funkcja f ( x ) = ax jest malejąca gdy 0 < a < 1.
Równania i nierówności wymierne:
- Jeżeli a > 0 i a ¹ 1 oraz ax = ay to x = y;
- Jeżeli a > 1 oraz ax > ay ( ax < ay ) to x > y ( x < y );
- Jeżeli a > 1 oraz ax ³ ay ( ax £ ay ) to x ³ y ( x £ y );
- Jeżeli 0 < a < 1 oraz ax > ay ( ax < ay ) to x < y ( x > y );
- Jeżeli 0 < a < 1 oraz ax ³ ay ( ax £ ay ) to x £ y ( x ³ y ).
Logarytm dodatniej liczby b przy podstawie a ( a > 0 i a ¹ 1 ) jest to wykładnik potęgi, do której należy podnieść a, żeby otrzymać b:
log a b = z Û az = b.
Z określenia logarytmu wynika, że log a 1 = 0, log a a = 1.
Funkcją logarytmiczną jednej zmiennej nazywamy funkcję f: ( R+ ) ® R określoną wzorem postaci:
f ( x ) = log a x, gdzie aÎR+{1}.
Własności funkcji wymiernej:
- Funkcja f ( x ) = log a x jest rosnąca gdy a > 1;
- Funkcja f ( x ) = log a x jest malejąca gdy 0 < a < 1.
Twierdzenia o logarytmach:
- Jeśli a, b, cÎR+ i a ¹ 1, to log a (b×c) = log a b + log a c oraz log a
![]() = log a b - log a c;
= log a b - log a c; - Jeśli a, b ÎR+ , a ¹ 1 i rÎR, to log a br = r log a b;
- Jeśli a, b, xÎR+ , a ¹ 1 i b ¹ 1, to log a b =
![]() ( zmiana podstawy logarytmu ).
( zmiana podstawy logarytmu ).
6. Funkcje trygonometryczne
Jeśli a jest miarą kąta skierowanego 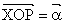 , P jest dowolnym punktem końcowego ramienia tego kąta ( P ¹ O, x i y są współrzędnymi P,
, P jest dowolnym punktem końcowego ramienia tego kąta ( P ¹ O, x i y są współrzędnymi P, 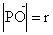 , to
, to
sin a = 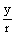 , cos a =
, cos a = 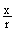 , tg a =
, tg a = 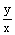 ( gdy x ¹ 0 ), ctg a =
( gdy x ¹ 0 ), ctg a = 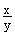 ( gdy y ¹ 0 ).
( gdy y ¹ 0 ).
Związki między funkcjami tego samego kąta x:
sin2x + cos2x = 1, dla xÎ R,
tg x = 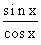 , dla x ¹(2k+1)×
, dla x ¹(2k+1)×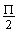 , kÎC,
, kÎC,
ctg x = 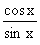 , dla x ¹ kP, kÎC,
, dla x ¹ kP, kÎC,
tg x × ctg x = 1, dla x¹k×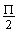 , kÎC.
, kÎC.
Funkcje trygonometryczne kąta podwójnego:
sin 2x = 2×sin x×cos x,
cos 2x = cos2x - sin2x = 1 - 2sin2x = 2 cos2x – 1,
tg 2x = 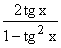 , dla x¹(2k+1)×
, dla x¹(2k+1)×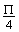 i x¹(2k+1)×
i x¹(2k+1)×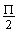 , kÎC,
, kÎC,
ctg 2x = 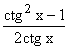 , dla x¹k×
, dla x¹k×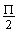 , kÎC.
, kÎC.
Funkcje trygonometryczne to funkcje okresowe. Okresem zasadniczym funkcji sinus i cosinus jest 2P, a okresem zasadniczym funkcji tangens i cotangens jest P.
Równania trygonometryczne są to równania, w których niewiadome występują pod znakami funkcji trygonometrycznych.
Tabela zawiera rozwiązania najprostszych równań trygonometrycznych:
|
Równanie
| Rozwiązanie |
x0 jedyne rozwiązanie równania należące do przedziału
|
|
sin x = a, |a|<1
|
x = kP+(-1)kx0, kÎC
|
|
|
cos x = a, |a|<1
|
x = 2kP ± x0, kÎC
|
( 0, P )
|
|
tg x = a, aÎR
|
x = kP + x0, kÎC
|
|
|
ctg x = a, aÎR
|
x = kP + x0, kÎC
|
|
7. Funkcje wymierne. Równania i nierówności wymierne.
Funkcją wymierną jednej zmiennej nazywamy funkcję F: ( R A ) ® R określoną wzorem postaci:
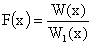 ,
,
gdzie W i W1 są wielomianami, zaś A jest zbiorem wszystkich miejsc zerowych wielomianu W1.
Równaniem wymiernym nazywamy równanie postaci:
![]() ,
,
gdzie W i W1 są wielomianami.
Rozwiązaniem równania ![]() nazywamy każdą liczbę r, dla której W1(r)¹0 i W(r)=0.
nazywamy każdą liczbę r, dla której W1(r)¹0 i W(r)=0.
Nierównością wymierną nazywamy nierówność postaci
![]() , lub
, lub ![]() , lub
, lub ![]() , lub
, lub ![]() ,
,
gdzie W i W1 są wielomianami.
Nierówności
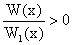 ,
, 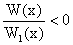
są równoważne odpowiednio nierównościom w postaci iloczynu:
W(x)×W1(x)>0, W(x)×W1(x)<0.
Natomiast nierówności
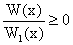 ,
, 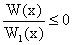
są równoważne odpowiednio układom:
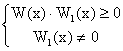 ,
, 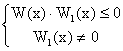 .
.
8. Ciągi
Zasada indukcji matematycznej ( zupełnej )
Jeżeli twierdzenie, które dotyczy liczb naturalnych, jest
(1. prawdziwe dla ustalonej liczby naturalnej n0,
(2. jeżeli dla każdej liczby naturalnej k ³ n0 z założenia prawdziwości twierdzenia dla k wynika, że jest ono prawdziwe dla liczby następnej k + 1,
to twierdzenie jest prawdziwe dla każdej liczby naturalnej n ³ n0.
Ciągiem nieskończonym nazywamy funkcję określoną na zbiorze liczb naturalnych dodatnich ( N { 0 } ). Wartości tej funkcji nazywamy wyrazami ciągu i oznaczamy f ( n ) = an. Jeżeli wyrazy ciągu są liczbami rzeczywistymi , to ciąg nazywamy ciągiem liczbowym.
Ciąg o wyrazach a1, a2,..., an, ... oznaczamy ( an ).
Ciąg liczbowy ( an ) nazywamy:
- ciągiem rosnącym wtedy i tylko wtedy gdy dla każdego nÎN{0} zachodzi an < an+1;
- ciągiem malejącym wtedy i tylko wtedy gdy dla każdego nÎN{0} zachodzi an > an+1;
- ciągiem niemalejącym wtedy i tylko wtedy gdy dla każdego nÎN{0} zachodzi an £ an+1;
- ciągiem nierosnącym wtedy i tylko wtedy gdy dla każdego nÎN{0} zachodzi an ³ an+1.
Ciągi rosnące lub malejące nazywamy monotonicznymi.
Granice ciągu
Liczba g jest granicą ciągu liczbowego ( an ) wtedy i tylko wtedy, gdy do każdego otoczenia liczby g należą wszystkie wyrazy tego ciągu z wyjątkiem skończonej ich ilości.
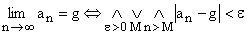 .
.
Ciąg liczbowy ( an ) jest rozbieżny do +¥ wtedy i tylko wtedy, gdy dla każdej liczby A wszystkie wyrazy tego ciągu oprócz skończonej ich ilości są większe od A..
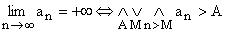 .
.
Ciąg liczbowy ( an ) jest rozbieżny do -¥ wtedy i tylko wtedy, gdy dla każdej liczby B wszystkie wyrazy tego ciągu oprócz skończonej ich ilości są mniejsze od B..
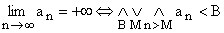 .
.
Prawdziwe są następujące twierdzenia:
- Jeżeli
![]() i
i ![]() , to:
, to:
a) 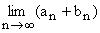 = a + b, b)
= a + b, b) 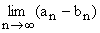 = a – b,
= a – b,
c) 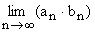 = a × b, d) jeżeli
= a × b, d) jeżeli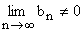 , to
, to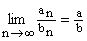 .
.
- Jeżeli dla każdego nÎN{0} an > 0 i
![]() , to
, to ![]() .
. - Jeżeli dla każdego nÎN{0} an < 0 i
![]() , to
, to ![]() .
. - Jeżeli
![]() , to
, to ![]() .
. - Jeżeli
![]() i ciąg ( bn ) jest ciągiem ograniczonym, to
i ciąg ( bn ) jest ciągiem ograniczonym, to![]() .
.
9. Ciągi arytmetyczny i geometryczny
Ciąg arytmetyczny
Ciąg ( an ) nazywamy arytmetycznym wtedy i tylko wtedy, gdy różnica między dowolnym wyrazem ciągu a wyrazem bezpośrednio go poprzedzającym, jest stała dla danego ciągu.
an+1 - an = r
Dla dowolnego ciągu ( an ) przez Sn oznaczamy sumę pierwszych n wyrazów tego ciągu, tzn.
Sn = a1 + a2 + ... + an.
Jeżeli ciąg ( an ) jest ciągiem arytmetycznym o różnicy r, to prawdziwe są wzory:
- dla każdego nÎN{0} an = a1 + ( n – 1 ) r,
- dla każdego nÎN{0} an =
![]() ,
, - dla każdego nÎN{0} Sn =
![]() =
= ![]() .
.
Ciąg geometryczny
Ciąg ( an ) nazywamy geometrycznym wtedy i tylko wtedy, gdy a1 ¹ 0 i iloraz dowolnego wyrazu tego ciągu i wyrazu bezpośrednio go poprzedzającego, jest dla danego ciągu stały.
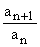 = q
= q
Jeżeli ciąg ( an ) jest ciągiem geometrycznym o ilorazie q ¹ 0, to prawdziwe są wzory:
- dla każdego nÎN{0} an = a1 ×qn-1,
- dla każdego nÎN{0} an2 = an-1×an+1,
- jeżeli q ¹ 1, to Sn = a1
![]() ,
, - jeżeli q = 1, to Sn = n × a1.
Dla ciągu geometrycznego ( an ) spełniającego warunek ½q½ < 1 zachodzi:
-
![]() ,
, -
![]()
![]() .
.
10. Granica funkcji. Funkcje ciągłe.
1. Granica funkcji w punkcie
Liczba g jest granicą funkcji f w punkcie x0 wtedy i tylko wtedy, gdy dla każdego ciągu ( xn ) takiego, że xn Î Df , xn ¹ x0 i 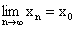 jest
jest 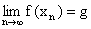 .
.
2. Granice jednostronne funkcji w punkcie
a) Liczbę a nazywamy granicą lewostronną funkcji f w punkcie x0 wtedy i tylko wtedy, gdy dla każdego ciągu ( xn ) spełniającego warunki xn Î Df , xn < x0 i 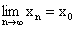 jest
jest 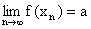 .
.
b) Liczbę b nazywamy granicą prawostronną funkcji f w punkcie x0 wtedy i tylko wtedy, gdy dla każdego ciągu ( xn ) spełniającego warunki xn Î Df , xn > x0 i 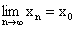 jest
jest 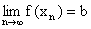 .
.
c) Istnienie granic jednostronnych funkcji w punkcie x0 i ich równość jest równoważna istnieniu granicy funkcji w punkcie x0.
3. Granica niewłaściwa funkcji w punkcie
a) Funkcja f ma w punkcie x0granicę niewłaściwą +¥ wtedy i tylko wtedy, gdy dla każdego ciągu ( xn ) takiego, że 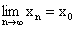 , xn Î Df i xn ¹ x0 jest
, xn Î Df i xn ¹ x0 jest 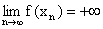 .
.
b) Funkcja f ma w punkcie x0granicę niewłaściwą -¥ wtedy i tylko wtedy, gdy dla każdego ciągu ( xn ) takiego, że 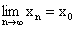 , xn Î Df i xn ¹ x0 jest
, xn Î Df i xn ¹ x0 jest 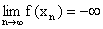 .
.
4. Twierdzenia o granicy funkcji w punkcie
Jeżeli 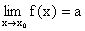 i
i 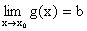 , to:
, to:
a) 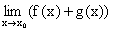 = a + b, b)
= a + b, b) 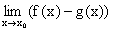 = a – b,
= a – b,
c) 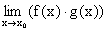 = a × b, d) jeżeli b¹0, to
= a × b, d) jeżeli b¹0, to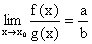 .
.
5. Granica funkcji w +¥ oraz w -¥
a) Mówimy, że granicą funkcji y = f(x) w +¥ jest liczba g wtedy i tylko wtedy, gdy dla każdego ciągu ( xn ) spełniającego warunki xn Î Df i 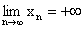 jest
jest 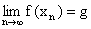 .
.
b) Mówimy, że granicą funkcji y = f(x) w -¥ jest liczba g wtedy i tylko wtedy, gdy dla każdego ciągu ( xn ) spełniającego warunki xn Î Df i 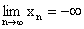 jest
jest 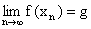 .
.
6. Ciągłość funkcji
Funkcja f jest ciągła w punkcie x0 Î Df wtedy i tylko wtedy, gdy istnieje granica funkcji w punkcie x0 i 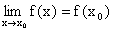 .
.
Funkcja f jest ciągła w zbiorze Z Ì Df wtedy i tylko wtedy, gdy jest ciągła w każdym punkcie zbioru Z.
Jeżeli funkcje f i g są ciągłe w punkcie x0, to funkcje f + g, f - g, f × g też są ciągłe w tym punkcie, i jeżeli g(x0) ¹ 0, to funkcja 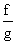 też jest ciągła w x0.
też jest ciągła w x0.
11. Pochodna funkcji i jej zastosowania
Ilorazem różnicowym funkcji f odpowiadającym przyrostowi argumentu Dx = x1 – x0, gdzie x0, x1Î Df i x0 ¹ x1, nazywamy liczbę 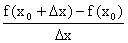 .
.
Jeżeli przy powyższym istnieje granica 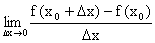 i jest liczba skończoną, to tę liczbę nazywamy pochodną funkcji w punkcie x0 i oznaczamy f ’(x0).
i jest liczba skończoną, to tę liczbę nazywamy pochodną funkcji w punkcie x0 i oznaczamy f ’(x0).
Jeżeli funkcja ma pochodną w punkcie x0, to mówimy, że jest w tym punkcie różniczkowalna.
Jeżeli funkcja y = f(x) jest określona w pewnym otoczeniu punktu x0 i ma w tym punkcie pochodną, to prosta o równaniu:
y = f ’(x) × ( x – x0 ) + f(x0)
jest prostą styczną do wykresu funkcji f w punkcie P ( x0, f(x0) ). f ’(x0) jest tangensem kąta nachylenia tej stycznej do osi 0X.
Jeżeli przez X oznaczymy zbiór tych argumentów, dla których istnieje pochodna funkcji f, wówczas funkcję, która każdemu x Î X przyporządkowuje liczbę f ’(x) nazywamy pochodną funkcji f. Dziedziną funkcji f ’ jest zbiór X.
Jeżeli funkcje f i g są różniczkowalne w zbiorze X, to:
a. ( k× f )’ = k × f ’, dla k Î R
b. ( f + g )’ = f ’ + g’
c. ( f - g )’ = f ’ - g’
d. ( f × g )’ = f ’× g + g’× f
e. 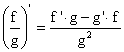
Pochodne niektórych funkcji:
- ( c )’ = 0
- ( x m )’ = m xm-1, dla m Î W {0}
- ( sin x )’ = cos x
- ( cos x )’ = - sin x
e. ( tg x )’ = 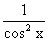
f. ( ctg x )’ = - 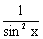
Jeśli funkcja f jest różniczkowalna w każdym punkcie pewnego zbioru X Ì R, a funkcja g w każdym punkcie y0 = f(x) zbioru wartości funkcji f, to dla x Î X pochodna funkcji złożonej h = g ◦ f równa się iloczynowi pochodnej funkcji zewnętrznej g i pochodnej funkcji wewnętrznej f:
( g ◦ f )’(x) = g’(f(x)) × f ’(x).
Jeżeli funkcja f jest różniczkowalna w zbiorze Z Ì Df i pochodna funkcji f jest różniczkowalna, to pochodną funkcji f ’ nazywamy drugą pochodną funkcji f i oznaczamy f ’’.
12. Badanie funkcji
1. Twierdzenia o monotoniczności funkcji
Niech funkcja f będzie różniczkowalna w przedziale ( a, b ), wtedy dla każdego x Î ( a, b )
- jeżeli f ’(x) > 0, to funkcja f jest rosnąca w przedziale ( a, b );
- jeśli f jest rosnąca w przedziale ( a, b ), to f ’(x) ³ 0;
- jeżeli f ’(x) < 0, to funkcja f jest malejąca w przedziale ( a, b );
- jeśli f jest malejąca w przedziale ( a, b ), to f ’(x) £ 0.
2. Ekstremum funkcji
Mówimy, że funkcja ma w punkcie x0 Î Dfminimum ( maksimum ), jeśli dla każdego x należącego do pewnego otoczenia punktu x0 zawartego w dziedzinie funkcji zachodzi f(x) > f(x0)
( f(x) < f(x0) ). Maksimum i minimum nazywamy ekstremum funkcji.
Warunek konieczny ekstremum. Jeżeli funkcja f ma ekstremum w punkcie x0 Î ( a, b ) i jest w tym punkcie różniczkowalna, to
f ’(x0) = 0.
Warunek wystarczający ekstremum. Jeżeli funkcja f ma pochodną w pewnym otoczeniu punktu x0, przy czym
f ’(x) > 0 gdy x < x0 i f ’(x) < 0 gdy x > x0
to w punkcie x0 funkcja f ma maksimum; jeżeli natomiast
f ’(x) < 0 gdy x < x0 i f ’(x) > 0 gdy x > x0
to w punkcie x0 funkcja f ma minimum.
3. Najmniejsza i największa wartość funkcji w przedziale
Mówimy, że funkcja f określona w przedziale < a, b > osiąga w tym przedziale wartość największą ( najmniejszą ), jeśli istnieje punkt x0 Î < a, b > taki, że dla każdego x Î < a, b > i x ¹ x0 spełniony jest warunek f(x) £ f(x0) ( f(x) ³ f(x0) ).
Aby wyznaczyć największą ( najmniejszą ) wartość funkcji w przedziale < a, b >, należy znaleźć wszystkie maksima ( minima ) lokalne w tym przedziale oraz obliczyć f(a) i f(b); największa ( najmniejsza ) z tych liczb jest liczbą poszukiwaną.
4. Asymptoty wykresu funkcji
Prostą, której odległość od wykresu danej funkcji f zmierza do zera w nieskończoności nazywamy asymptotą wykresu funkcji f.
Prostą o równaniu x = a nazywamy asymptotą pionową wykresu funkcji f, jeżeli funkcja f jest określona przynajmniej z jednej strony punktu a oraz 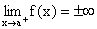 albo
albo 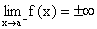 .
.
Jeżeli istnieją skończone granice 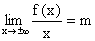 oraz
oraz 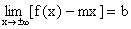 , to prostą o równaniu y = mx+b nazywamy asymptotą ukośną ( albo poziomą przy m = 0 ) wykresu funkcji f.
, to prostą o równaniu y = mx+b nazywamy asymptotą ukośną ( albo poziomą przy m = 0 ) wykresu funkcji f.
12. Badanie funkcji cd.
5. Schemat badania funkcji
5.1 Wyznaczamy dziedzinę funkcji
5.2 Obliczamy granice na końcach dziedziny
5.3 Wyznaczamy asymptoty wykresu funkcji
5.4 Wyznaczamy pierwszą pochodną i jej dziedzinę
5.5 Obliczamy miejsca zerowe pierwszej pochodnej
5.6 Określamy znak pierwszej pochodnej, wyznaczamy przedziały monotoniczności i ekstrema
funkcji
5.7 Wyznaczamy punkty przecięcia wykresu funkcji z osiami układu współrzędnych i wartości
funkcji w punktach wyznaczonych w 5.5, 5.6
5.8 Zbieramy wyniki z poprzednich punktów w tabeli
5.9 Szkicujemy wykres funkcji
13. Funkcja homograficzna
Funkcją homograficzną nazywamy funkcję postaci
f(x) = 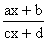
gdzie c ¹ 0 i a×d - b×c ¹ 0.
Dziedziną funkcji homograficznej jest zbiór D = 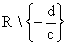 .
.
Wykresem funkcji homograficznej jest hiperbola.
Proste o równaniach x = 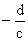 oraz y =
oraz y = 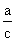 są asymptotami tej hiperboli.
są asymptotami tej hiperboli.
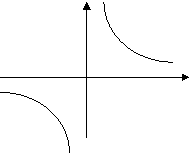 | 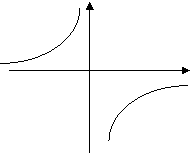 |
hiperbola o równaniu y = 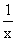 hiperbola o równaniu y = -
hiperbola o równaniu y = -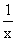
Aby narysować funkcję homograficzną musimy jej postać f(x) = 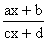 przekształcić do postaci f(x) =
przekształcić do postaci f(x) = 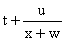 , wtedy wykres funkcji y =
, wtedy wykres funkcji y = 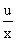 przesuwamy o wektor [ -w, t ].
przesuwamy o wektor [ -w, t ].
Pochodna funkcji homograficznej jest równa f ’(x) = 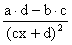 , ponieważ z założenia licznik jest różny od zera, więc pochodna funkcji nie przyjmuje wartości równej zero, czyli funkcja homograficzna nie posiada ekstremum. Znak pochodnej zależy od znaku licznika ( czyli wyrażenia a×d - b×c ). Wynika z tego, że:
, ponieważ z założenia licznik jest różny od zera, więc pochodna funkcji nie przyjmuje wartości równej zero, czyli funkcja homograficzna nie posiada ekstremum. Znak pochodnej zależy od znaku licznika ( czyli wyrażenia a×d - b×c ). Wynika z tego, że:
funkcja homograficzna jest w przedziałach ( -¥, 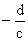 ) oraz (
) oraz ( 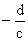 , +¥ ) rosnąca, gdy a×d - b×c > 0, funkcja homograficzna jest w przedziałach ( -¥,
, +¥ ) rosnąca, gdy a×d - b×c > 0, funkcja homograficzna jest w przedziałach ( -¥, 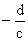 ) oraz (
) oraz ( 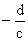 , +¥ ) malejąca, gdy a×d - b×c < 0.
, +¥ ) malejąca, gdy a×d - b×c < 0.
14. Geometria analityczna – wektory, proste
Współrzędnymi wektora 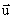 w prostokątnym układzie współrzędnych XOY nazywamy miary jego składowych. Jeżeli punkt A( xA, yA ) jest początkiem, a punkt B( xB, yB ) jest końcem wektora
w prostokątnym układzie współrzędnych XOY nazywamy miary jego składowych. Jeżeli punkt A( xA, yA ) jest początkiem, a punkt B( xB, yB ) jest końcem wektora 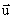 , to współrzędnymi wektora
, to współrzędnymi wektora 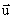 są liczby: a = xB - xA , b = yB - yA .
są liczby: a = xB - xA , b = yB - yA .
Zapisujemy to symbolicznie: 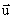 [ a, b ] lub
[ a, b ] lub 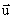 = [ a, b ].
= [ a, b ].
Jeżeli wektor 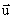 = [ a, b ], to długość wektora
= [ a, b ], to długość wektora 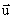 wyraża się wzorem:
wyraża się wzorem: 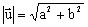 .
.
Jeżeli punkt A( xA, yA ) i punkt B( xB, yB ), to środek S odcinka 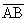 ma współrzędne:
ma współrzędne:
xS =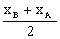 , yS =
, yS = 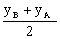 .
.
Jeśli a jest miarą kąta skierowanego uporządkowanej pary niezerowych wektorów ( 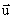 ,
, 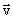 ) współrzędnych
) współrzędnych 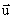 = [ a1, a2 ],
= [ a1, a2 ], 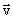 = [b1, b2 ], to:
= [b1, b2 ], to:
cos a = 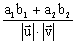 , sin a =
, sin a = 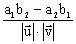 .
.
Jeżeli wektory 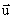 i
i 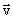 mają współrzędne
mają współrzędne 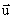 = [ a1, a2 ],
= [ a1, a2 ], 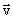 = [b1, b2 ], to ich iloczyn skalarny wyraża się wzorem
= [b1, b2 ], to ich iloczyn skalarny wyraża się wzorem 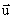 ×
×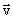 = a1 × b1 + a2 × b2 .
= a1 × b1 + a2 × b2 .
Wyznacznikiem niezerowej pary wektorów 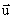 i
i 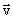 o współrzędnych
o współrzędnych 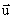 = [ a1, a2 ],
= [ a1, a2 ], 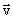 = [b1, b2 ] nazywamy liczbę d(
= [b1, b2 ] nazywamy liczbę d( 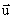 ,
, 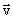 ) =
) = 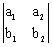 = a1 × b2 - a2 × b1 .
= a1 × b2 - a2 × b1 .
Jeżeli punkty A( xA, yA ), B( xB, yB ) i C( xC, yC ) są wierzchołkami trójkąta, to pole trójkąta DABC wyraża się wzorami:
P = 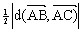 =
=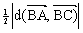 =
=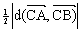 ,
,
P = 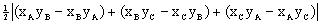 .
.
Współczynnikiem kierunkowym prostej nieprostopadłej do osi OX nazywamy tangens kąta nachylenia tej prostej do osi OX.
Równaniem kierunkowym prostej l nieprostopadłej do osi OX nazywamy równanie postaci y = ax+b, gdzie a oznacza współczynnik kierunkowy prostej l, zaś b rzędną punktu, w którym l przecina oś OY.
Jeżeli punkty A( xA, yA ) i B( xB, yB ) należą do prostej l, to równanie prostej l ma postać:
y - yA = 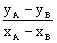 ( x – xA ), gdy xA ¹ xB , lub
( x – xA ), gdy xA ¹ xB , lub
( y - yA )×( xA – xB ) – ( yA – yB )×( x – xA ) = 0.
Każde równanie postaci Ax+By+C = 0, gdzie A2 +B2 ¹ 0 jest równaniem ogólnym prostej. Wektor 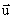 = [ A, B ] jest wektorem prostopadłym do tej prostej.
= [ A, B ] jest wektorem prostopadłym do tej prostej.
Odległość punktu P ( x0, y0 ) od prostej o równaniu Ax+By+C = 0 wyraża się wzorem:
d = 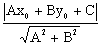 .
.
Warunki równoległości prostych
Dwie proste o równaniach y = a1 x +b1 i y = a2 x +b2 są równoległe wtedy i tylko wtedy, gdy a1 = a2.
Dwie proste o równaniach Ax+By+C = 0 i A1 x+B1 y+C1 = 0 są równoległe wtedy i tylko wtedy, gdy
AB1 – BA1 = 0.
Warunki prostopadłości prostych
Dwie proste o równaniach y = a1 x +b1 i y = a2 x +b2 są prostopadłe wtedy i tylko wtedy, gdy a1 × a2 = -1.
Dwie proste o równaniach Ax+By+C = 0 i A1 x+B1 y+C1 = 0 są prostopadłe wtedy i tylko wtedy, gdy
AA1 + BB1 = 0.
15. Geometria analityczna – krzywe stopnia drugiego
Okrąg
Równanie okręgu o środku ( a, b ) i promieniu r ma postać ( x – a )2 + ( y – b )2 = r 2 .
Równanie postaci x2 + y2 -2ax – 2by + c = 0 przedstawia okrąg wtedy i tylko wtedy, gdy a2 +b2 – c > 0, promieniem okręgu jest r = 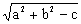 , zaś środkiem punkt ( a, b ).
, zaś środkiem punkt ( a, b ).
Równanie stycznej do okręgu o środku ( a, b ) i promieniu r w punkcie ( x0, y0 ) należącym do okręgu, ma postać ( x0 – a )( x – a )+( y0 – b )( y – b ) = r 2 .
Elipsa
Niech dane będą dwa punkty F1, F2 oraz liczba dodatnia a taka, że 2a > F1×F2 . Elipsą nazywamy zbiór tych wszystkich punktów P płaszczyzny, dla których PF1 + PF2 = 2a.
Jeśli punkty F1, F2 należą do osi OX, zaś początek układu współrzędnych jest środkiem odcinka 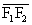 , to równanie elipsy ma postać
, to równanie elipsy ma postać 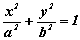 , gdzie b2 = a2 – c2 i |c| = OF1 .
, gdzie b2 = a2 – c2 i |c| = OF1 .
Elipsa ta ma środek symetrii w punkcie ( 0, 0 ) i dwie osie symetrii proste OX i OY.
Równanie stycznej do elipsy w punkcie ( x0, y0 ) należącym do elipsy, ma postać: 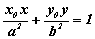 .
.
Punkty F1, F2 nazywamy ogniskami elipsy.
Cięciwą elipsy nazywamy każdy odcinek, którego końce należą do elipsy. Średnicą elipsy nazywamy każdą cięciwę, do której należy środek symetrii elipsy. Osią wielką nazywamy najdłuższą z jej średnic. Osią małą nazywamy najkrótszą z jej średnic. Wierzchołkami elipsy nazywamy punkty wspólne elipsy i jej osi symetrii.
Mimośrodem elipsy nazywamy liczbę e = 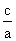 , zaś kierownicami elipsy proste o równaniach:
, zaś kierownicami elipsy proste o równaniach:
x = 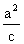 i x = -
i x = -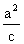 .
.
Hiperbola
Niech dane będą dwa punkty F1, F2 oraz liczba dodatnia a taka, że 2a < F1×F2 . Hiperbolą nazywamy zbiór tych wszystkich punktów P płaszczyzny, dla których ½PF1 - PF2 ½= 2a.
Jeśli punkty F1, F2 należą do osi OX, zaś początek układu współrzędnych jest środkiem odcinka 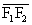 , to równanie hiperboli ma postać
, to równanie hiperboli ma postać 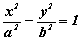 , gdzie b2 = c2 – a2 i |c| = OF1.
, gdzie b2 = c2 – a2 i |c| = OF1.
Hiperbola ta ma środek symetrii w punkcie ( 0, 0 ) i dwie osie symetrii proste OX i OY.
Równanie stycznej do hiperboli w punkcie ( x0, y0 ) należącym do hiperboli, ma postać: 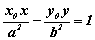 .
.
Punkty F1, F2 nazywamy ogniskami hiperboli.
Asymptotami hiperboli są elipsy proste o równaniach: y = 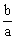 ×x i y = -
×x i y = -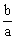 ×x.
×x.
Parabola
Jest to krzywa, która w pewnym układzie XOY ma równanie y2 = 2px, gdzie p ¹ 0, 2p jest parametrem paraboli. Punkt F = 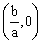 jest ogniskiem paraboli. Prosta o równaniu x = -
jest ogniskiem paraboli. Prosta o równaniu x = -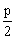 jest kierownicą paraboli. Punkt ( 0, 0 ) jest wierzchołkiem paraboli.
jest kierownicą paraboli. Punkt ( 0, 0 ) jest wierzchołkiem paraboli.
Parabola jest zbiorem wszystkich punktów płaszczyzny równo odległych od jej ogniska i od jej kierownicy. Jedyną osią symetrii paraboli jest prosta OX.
Równanie stycznej do paraboli y2 = 2px w punkcie ( x0, y0 ) należącym do paraboli, ma postać:
y × y0 = p× ( x + x0 ).
16. Planimetria - własności podstawowych figur planimetrycznych
Odległość punktu od prostej.
Odległość punktu od figury niepustej – długość promienia największego otoczenia kołowego tego punktu wewnątrz którego nie ma punktów tej figury. Gdy otoczenie takie nie istnieje, odległość jest zerem.
Odległość punktu od prostej równa się odległości tego punktu od jego rzutu prostokątnego na tę prostą.
Położenie prostej m względem okręgu o(A,r).
m jest styczną do o(A,r) Û odl. A od m = r,
m jest sieczną o(A,r) Û odl. A od m < r,
m jest zewnętrzną dla o(A,r) Û odl. A od m > r.
Styczna do okręgu (tzn. prosta mająca z nim dokładnie jeden punkt wspólny) jest prostopadła do promienia łączącego punkt styczności ze środkiem okręgu.
Dwa okręgi.
Jeśli okręgi o(A,a) i o(B,b) są różne i a ³ b, to
o(A,a) i o(B,b) są wzajemnie zewnętrzne Û AB > a + b,
o(A,a) i o(B,b) są zewnętrznie styczne Û AB = a + b,
o(A,a) i o(B,b) przecinają się Û a - b < AB < a + b,
o(A,a) i o(B,b) są wewnętrznie styczne Û a - b = AB,
o(B,b) Ì k(A,a) Û a - b > AB.
Związki miarowe w trójkącie prostokątnym.
Jeśli 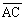 ^
^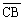 i
i 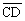 ^
^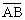 , to a2 =
, to a2 =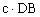 , sina=
, sina=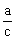 , cosa=
, cosa=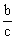 , tga=
, tga=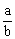 , ctga=
, ctga=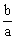 , b2 =
, b2 =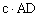 , a=
, a=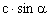 =
=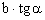 , h2 =
, h2 =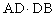 , b=
, b=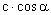 =
=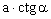 , c2 = a2+b2 (tw. Pitagorasa), c=
, c2 = a2+b2 (tw. Pitagorasa), c=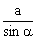 =
=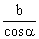 .
.
Związki miarowe w dowolnym trójkącie.
Wzór sinusów: 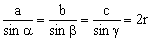 , gdzie r – długość promienia okręgu opisanego na DABC.
, gdzie r – długość promienia okręgu opisanego na DABC.
Wzór cosinusów: a2 = b2 + c2 - 2bc cosa.
Symetralne wszystkich boków trójkąta przecinają się w jednym punkcie O, który jest środkiem okręgu przechodzącego przez punkty A, B, C, czyli okręgu opisanego na tym trójkącie.
Długość promienia opisanego na trójkącie r =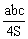 , gdzie S jest polem trójkąta;
, gdzie S jest polem trójkąta;
Dwusieczne wszystkich kątów wewnętrznych trójkąta przecinają się w jednym punkcie, który jest środkiem okręgu stycznego do wszystkich boków trójkąta, czyli okręgu wpisanego w trójkąt.
Długość promienia okręgu wpisanego w trójkąt 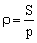 , gdzie S – pole, p – połowa obwodu trójkąta.
, gdzie S – pole, p – połowa obwodu trójkąta.
Odcinek łączący środki dwu boków trójkąta jest równoległy do trzeciego boku i równy jego połowie.
16. Planimetria - własności podstawowych figur planimetrycznych cd.
Najważniejsze wiadomości o wielokątach.
Czworokąt – wielokąt o czterech bokach.
Suma miar kątów wewnętrznych dowolnego czworokąta jest równa 360O.
Trapez – czworokąt mający przynajmniej dwa boki równoległe.
Trapez równoramienny – trapez mający dwa boki przeciwległe nierównoległe i równe.
Jeżeli w trapezie dwa przeciwległe boki nie są równoległe, to
1. suma kątów wewnętrznych leżących przy każdym z tych boków jest kątem półpełnym,
2. odcinek łączący środki tych boków jest równoległy do podstaw (tzn. boków równoległych), a jego długość równa się połowie sumy długości obu podstaw.
W trapezie równoramiennym kąty przy każdej podstawie są przystające.
Trapez równoramienny ma jedną oś symetrii.
Czworokąt wpisany w okrąg i czworokąt opisany w kręgu.
Czworokąt wypukły można wpisać w krąg Û sumy miar kątów przeciwległych w tym czworokącie są równe(każda z nich jest równa 180o).
Czworokąt wypukły można opisać na kręgu Û sumy długości boków przeciwległych w tym czworokącie są równe.
Odcinki, proste i kąty w związku z okręgiem
Kąt między cięciwą i styczną
Kąt ostry między cięciwą i styczną przechodzą przez koniec cięciwy jest równy połowie kąta środkowego opowiadającego cięciwie.
Kąt środkowy i kąty wpisane oparte na tym samym łuku
Wszystkie kąty wpisane okrąg i oparte na tym samym łuku są równe każdy z nich jest równy połowie kąta środkowego opartego na tym łuku
Kąt wpisany w półokrąg (oparty na średnicy) jest prosty.
17. Rachunek prawdopodobieństwa
Kombinatoryka
Permutacje – każdy n - wyrazowy ciąg utworzony ze wszystkich elementów n elementowego zbioru. P = n!
Kombinacje – każdy k - elementowy podzbiór n - elementowego zbioru. 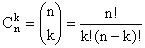
Wariacje bez powtórzeń – każdy k - wyrazowy ciąg utworzony z różnych elementów n - elementowego zbioru. 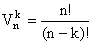
Wariacje z powtórzeniami – każdy k - wyrazowy ciąg utworzony z elementów n - elementowego zbioru. 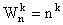
Własności prawdopodobieństwa
P(A) ³ 0, P(Æ) = 0, P(W) = 1,
jeżeli A Ì B to P(A) £ P(B), dla każdego A Ì W jest P(A) £1,
P(A’) = 1- P(A), P(AÈB) = P(A) + P(B) – P(AÇB).
Klasyczna definicja prawdopodobieństwa
Jeżeli wszystkie zdarzenia elementarne są jednakowo prawdopodobne to prawdopodobieństwo każdego zdarzenia A jest ilorazem liczby zdarzeń sprzyjających temu zdarzeniu przez liczbę wszystkich zdarzeń elementarnych. P(A) = 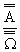 ,
,
gdzie 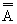 - liczba zdarzeń sprzyjających zdarzeniu A,
- liczba zdarzeń sprzyjających zdarzeniu A, 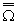 - liczba wszystkich zdarzeń elementarnych.
- liczba wszystkich zdarzeń elementarnych.
Prawdopodobieństwo warunkowe
Prawdopodobieństwo zdarzenia A pod warunkiem zajścia zdarzenia B jest to liczba
P(A / B) = 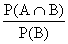
Prawdopodobieństwo całkowite ( zupełne )
Jeśli B1, B2, ... ,Bn są zdarzeniami wyłączającymi się parami oraz ich suma jest zdarzeniem pewnym, to dla dowolnego zdarzenia A zachodzi wzór:
P(A) = P(A / B1) × P(B1) + P(A / B2) × P(B2) + ... + P(A / Bn) × P(Bn)
Niezależność zdarzeń
Zdarzenia A i B nazywamy niezależnymi, jeżeli P(AÇB) = P(A) × P(B).
W przeciwnym przypadku mówimy, że zdarzenia A i B są zależne.
Schemat Bernoulliego – ciąg powtórzeń tego samego doświadczenia
Prawdopodobieństwo otrzymania dokładnie k sukcesów w n próbach Bernoulliego wynosi:
Pn(k) = 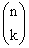 ×pk×qn-k,
×pk×qn-k,
gdzie p – prawdopodobieństwo sukcesu, q = 1- p - prawdopodobieństwo porażki, k = 0, 1, ... ,n.

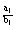 x +
x + 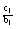 ;
;
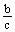 = log a b - log a c;
= log a b - log a c;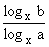 ( zmiana podstawy logarytmu ).
( zmiana podstawy logarytmu ).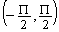
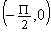 È
È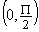
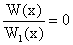 ,
,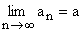 i
i 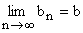 , to:
, to: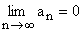 , to
, to 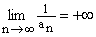 .
.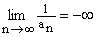 .
.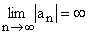 , to
, to 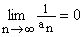 .
.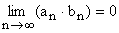 .
.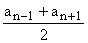 ,
,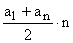 =
= 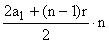 .
.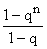 ,
,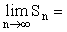
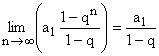 .
.
