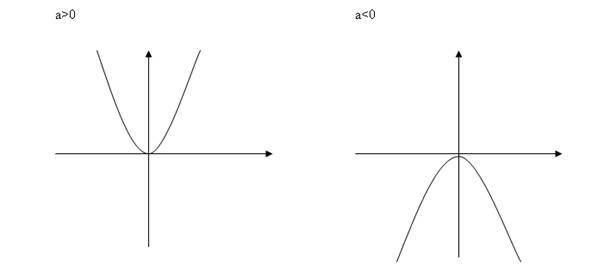
1. Jednomian drugiego stopnia: f(x)=ax2
Wykres:
2. Trójmian kwadratowy
Trójmian kwadratowy ma postać: f(x)=ax2+bx+c, gdzie a jest różne od zera, i a, b, c należą do zbioru liczb rzeczywistych.
Wyrażenie Δ=b2-4ac nazywane jest wyróżnikiem trójmianu.
Gdy a=0, trójmian redukuje się do zwykłego wzoru funkcji liniowej, która ma postać f(x)=bx+c. Rozwiązaniem równania bx+c=0 jest wtedy wartość x=-c/b, o ile b jest różne od zera.
Gdy a jest różne od zera i wyróżnik Δ jest dodatni, to równanie ax2+bx+c=0 posiada dwa pierwiastki: x1,2=(-b±√Δ)/2a, gdzie √ oznacza pierwiastek kwadratowy
Gdy a jest różne od zera i wyróżnik jest ujemny, równanie ax2+bx+c=0 nie ma rozwiązań w zbiorze liczb rzeczywistych.
Gdy a jest różne od zera a wyróżnik równy zeru, równanie ax2+bx+c=0 posiada dokładnie jedno rozwiązanie równe -b/(2a).
Ogólna postać trójmianu to f(x)= ax2+bx+c.
Postacią kanoniczną jest postać f(x)=a(x-p)^2+q, gdzie p=-b/(2a), q=-Δ/(4a).
Postać iloczynowa trójmianu: f(x)=a(x-x1)(x-x2) dla wyróżnika Δ dodatniego, oraz f(x)=a(x-x0)^2 dla wyróżnika Δ równego zero (x0 jest pierwiastkiem).
Istnieją wzory na sumę i iloczyn pierwiastków trójmianu. Noszą one nazwę wzorów Viete'a.
Jeśli Δ>0, to x1+x2= -b/a, x1*x2= c/a.


