Dawno, dawno temu w dalekiej krainie, w czasach gdy największą rozrywką władców były turnieje rycerskie, żył król, który się na nich nudził. Nie uprzyjemniały mu również czasu ani konne przejażdżki, ani fechtunek. Brak ciekawego zajęcia był na tyle nieznośny, że król postanowił ustalić wysoką nagrodę dla tego, kto zaciekawi go jakąś grą.
Któregoś dnia przybył na dwór króla starszy człowiek z innego kraju. Zaprezentował on królowi nową grę - szachy. Gra ta tak króla zachwyciła, że ten zadeklarował ofiarowanie mu wszystkiego, czego zażąda. Autor gry miał tylko jedno życzenie, które ilościowo wiązało się z szachami. Chciał tyle pszenicy ile zmieści się na szachownicy, przy czym ziarna miały być ułożone w następujący sposób: na pierwszym polu jedno ziarno, na drugim polu dwa ziarna, na trzecim 4 i w ten sposób na każde następne dwa razy więcej ziaren niż na poprzednim. Król bardzo się ucieszył, gdy usłyszał tak skromną, jak mu się wtedy wydawało, prośbę. Żeby wiedzieć ile to jest dokładnie, poprosił o podanie liczby worków, ale autorowi zależało na dokładnie takiej ilości ziaren. Ta prośba trochę rozbawiła króla, ale poszedł do nadwornych matematyków i nakazał im wyliczenie dokładnej ilości ziaren, jakiej oczekiwał cudzoziemiec. Gdy po zakończeniu obliczeń, matematycy podali królowi dokładną ilość ziaren, król się zasmucił, ponieważ okazało się, że takiej ilości ziarna nie ma w jego królestwie, a nawet nie wystarczyłoby gdyby zebrać całe ziarno z całego znanego wówczas świata.
Zastanówmy się ile ziaren oczekiwał cudzoziemiec:
Kładąc na pierwsze pole 1 ziarno, na drugie 2 ziarna, na trzecie 4 ziarna i tak dalej zauważymy, że ilość ziaren układa się w ciąg geometryczny. Ilość pól na szachownicy to 64. Zapiszmy ten ciąg w sposób taki, że a1 do a64 oznaczają ilość ziaren na kolejnych polach szachownicy. Popatrzmy:
a1 = 1 = 20
a2 = 2 = 21
a3 = 4 = 22
i tak dalej, aż do:
a64= 2(64-1) = 263
Jako, że jest to ciąg geometryczny, ilość wszystkich ziaren możemy obliczyć ze wzoru na sumę n wyrazów ciągu:
Sn = a1 * (1-q n) / (1-q)
W naszym przypadku:
S64 = 1 * (1-2 64) / (1-2) = 2 64 - 1
Przyjrzymy się ile wynoszą poszczególne wyrazy tej sumy:
22 = 4
24 = 42 = 16
210 = 1.024 - po 10 polach, mamy ponad tysiąc ziaren
220 = 1.048.576 - jak widać mamy już milion, a jeszcze nie ma nawet połowy obliczeń
240 = (220)2 = 1.099.511.627.776 - na czterdziestym polu mamy ponad bilion ziaren
260 = 240 * 220 = 1.152.901.504.600.846.976 - ponad milion bilionów, czyli ponad trylion
264 = 260 * 24 = 18.446.744.073.709.551.616 -ponad 18 trylionów
Pozostaje jeszcze kwestia, ile to jest worków?
Zakładając, że w jednym worku zmieści się około milion ziaren, to worków musiałoby być 18.446.744.073.709, czyli ponad 18 bilionów. Żeby przybliżyć w jakiś sposób tą liczbę, załóżmy, że w jednym wagonie zmieści się 100 worków i pociąg ma 100 wagonów, to tych pociągów z workami pszenicy trzeba zapełnić 184. Chociaż możemy sobie teraz wyobrazić taką ilość zboża, to widzimy, że zebranie takiej ilości ziarna, byłoby trudne nawet w dzisiejszych czasach.
 a) Stopa procentowa
a) Stopa procentowa
 b) Sumy algebraiczne
b) Sumy algebraiczne
 c) Siatka sześcianu
c) Siatka sześcianu
 d) Druga potęga
d) Druga potęga
 e) Równanie stopnia drugiego
e) Równanie stopnia drugiego
Zadanie 1
Wyobraźmy sobie sytuacje, w której człowiek prowadzi na smyczy psa w kierunku domu. Ich prędkość jest stała i wynosi 4 mile na godzinę. Gdy są oddaleni od domu o 10 mil, pan spuszcza psa ze smyczy, który biegnie do domu ze stałą prędkością 6 mil na godzinę. Gdy pies dobiegnie do domu, zawraca i biegnie z powrotem do pana z taką samą prędkością. Gdy do niego dobiegnie, zawraca do domu i tak biega do momentu, gdy pan nie dotrze do domu. Ile mil jest w stanie przebiec w ten sposób pies od momentu spuszczenia ze smyczy do wejścia z panem do domu?
Rozwiązanie:
Dane:
- Prędkość człowieka: Vc = 4 mile/h,
- Prędkość psa: Vp = 6 mil/h,
- Droga przebyta przez człowieka: Sc = 10 mil.
Szukane:
Droga przebiegu psa - Sp.
Rozwiązanie:
Przekształcamy wzór na prędkość
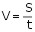
Obliczamy czas, jaki jest potrzebny człowiekowi na dotarcie do domu od momentu spuszczenia psa ze smyczy:
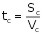
= 2,5 h.
Zakładając, że pies dotrze do domu wtedy co pan:
tp = tc = 2,5 h.
Otrzymamy rozwiązanie: Sp = Vp. tp = 6 . 2,5 = 15 mil
Zadanie 2
Podczas rozprawy gangstera sędzia wydał wyrok skazujący. Człowiek ten został skazany na powieszenie. Sędzia powiedział również, że wyrok zostanie wykonany w najbliższym tygodniu (dniem rozprawy była sobota), ale skazaniec nie może wiedzieć o dniu egzekucji wcześniej iż rankiem dnia w którym egzekucja zostanie przeprowadzona. Dlaczego wyrok nie może być wykonany w żaden dzień?
Rozwiązanie:
Ostatnim dniem, w którym można wykonać wyrok jest następna sobota. Jednakże w tym dniu nie może być on wykonany ponieważ, jeżeli skazaniec dożyłby tego dnia, to wiedziałby już dzień wcześniej, że to będzie sobota, bo jedyny ranek w którym mógłby się o tym dowiedzieć, byłby sobotni ranek. W piątek też nie można przeprowadzić egzekucji, ponieważ byłby to już ostatni dzień w którym można by tego dokonać z racji tego, że wykluczyliśmy już sobotę. Podobne rozumowanie możemy przeprowadzić dla pozostałych dni, stąd dostaniemy, że wyroku nie można wykonać w żaden dzień.
Zadanie 3
Mówi się, że zadanie to wymyślił Einstein i według niego większość ludzi na ziemi nie potrafi go rozwiązać, bo aż 98%.
Mamy pięć domów w pięciu kolorach, w każdym mieszka jeden człowiek. Każdy pali papierosy innej marki i pije inny napój. Każdy ma też inne zwierzę. Kto ma rybki?
- Norweg mieszka w pierwszym domu
- Anglik zamieszkuje czerwony dom
- Zielony dom jest po lewo od domu białego
- Duńczyk pije herbatę
- Palący Rothmansy mieszka koło hodowcy kotów
- Mieszkający w żółtym domu - pali Dunhille
- Niemiec pali - Marlboro
- Mieszkaniec domu w środku - pija mleko
- Palacz Rothmansów za sąsiada człowieka, który pija wodę
- Palący Pall Malli jest hodowcą ptaków
- Szwed ma psy
- Norweg mieszka koło niebieskiego domu
- Hodowca koni ma dom koło żółtego domu
- Palący Philip Morris pije piwo
- Mieszkaniec zielonego domu pije kawę
Rozwiązanie:
|
Dom1
|
Dom2
|
Dom3
|
Dom4
|
Dom5
| |
|
Narodowość:
|
Norweg
|
Duńczyk
|
Anglik
|
Niemiec
|
Szwed
|
|
Kolor domu
|
żółty
|
niebieski
|
czerwoni
|
zielony
|
|
|
Co pali ?
|
Dunhille
|
Rothams
|
Pall Mall
|
Marlboro
|
Philip Moris
|
|
Co pije ?
|
woda
|
herbata
|
mleko
|
kawa
|
piwo
|
|
Co hoduje ?
|
koty
|
konie
|
ptaki
|
RYBKI
|
psy
|
Zadanie 4
Na wyspie X mieszkają Rycerze i Łotry. Niczym się nie różnią, poza tym, że rycerze zawsze mówią prawdę, a Łotrzy kłamią.
1. Człowiek dostał się na wyspę X i spotkał na niej trzech mieszkańców. Pierwszemu zadał pytanie: Kim jesteś? ale ten odpowiedział mu niewyraźnie. Drugi powiedział, tłumacząc pierwszego, że tamten powiedział, że jest Łotrem, a na to odezwał się trzeci: nie wierz mu, on kłamie. Kim byli ludzie spotkani na wyspie X?
Człowieka na wyspie X goniła banda Łotrów, którzy czyhali na jego życie. Mądry człowiek z naszej cywilizacji chce dotrzeć do zamku ważnego Rycerza. Idąc lasem spotyka na rozstaju dróg 2 mieszkańców wyspy, z których jeden jest Łotrem, a drugi Rycerzem. Za nimi znajdują się dwie drogi, z których jedna jest właściwą drogą do zamku. Może zadać tylko jedno pytanie, jednemu mieszkańcowi. Jakie pytanie powinien zadać, aby wiedzieć, która droga jest właściwa do zamku? (nie będzie wiedział, którego z nich zapyta: Łotra czy Rycerza)
Rozwiązania:
1. Kluczowe w tej kwestii jest uświadomienie sobie, że na tej wyspie nikt nie powie o sobie, że jest Łotrem, ponieważ Rycerz powie prawdę, a Łotr skłamie mówiąc, że jest Rycerzem. Stąd wiemy na pewno, że druga osoba jest z pewnością Łotrem, a trzecia Rycerzem.
2. Powinien zadać pytanie: "Którą drogę wskazałby mi drugi mieszkaniec, gdybym go zapytał o drogę do zamku? Na tak postawione pytanie obydwaj pokazują na złą drogę.
Zadanie 5
Mamy czterech podróżnych, którzy chcą przejść nocą przez dziurawy most, ale mają tylko jedną latarkę. Nie chcą ryzykować przechodzenia bez latarki, ale jednocześnie na moście mogą znajdować się tylko 2 osoby. Kolejni podróżnicy mogą przejść przez most z następującą prędkością: jedna minuta, dwie minuty, pięć minut i dziesięć minut. Idąc w parze obydwaj idą z taką prędkością, jak wolniejszy. Jak wszyscy mogą się przedostać przez most w 17 minut?
Rozwiązanie:
Najpierw idzie podróżnik idący jedną minutę z podróżnikiem idącym dwie minuty. Następnie podróżnik idący jedną minutę wraca. Zajmuje im to w sumie 3 minuty.
Przechodzi przez most podróżnik idący pięć minut z podróżnikiem idącym dziesięć minut, natomiast wraca podróżnik idący 2 minuty. Zajmuje im to w sumie 12 minut.
Podróżnik idący minutę wraca z podróżnikiem idącym dwie minuty. Zajmuje im to 2 minuty.
W sumie dostajemy 17 minut.
Pitagoras (ok. 572-497 p. n. e)
Pitagoras urodził się na wyspie Samos. Gdy miał 40 lat opuścił Jonię będącą w stanie wojny z Persami, od tego czasu wiele podróżował, także do Indii. Był założycielem szkoły filozoficzno - religijnej w Krotonie oraz Związku Pitagorejskiego. Po Pitagorasie nie pozostały żadne dzieła, ale stworzył on system naukowych poglądów, które do dziś nazywamy jego imieniem. Prawdopodobnie to co przypisuje się Pitagorasowi, zostało wymyślone przez uczonych zwanych pitagorejczykami. Z literatury starogreckiej wnosimy, że Pitagoras był pierwszym, który użył określenia "miłość mądrości". Wprowadził również pojęcie dotyczące podobieństwa figur oraz pomysł a przeprowadzanie dowodów geometrycznych. Sam też przeprowadził dowód twierdzenia nazywanego dzisiaj twierdzeniem Pitagorasa.
Archimedes (ok. 287-212 p. n. e)
Opracował on wzory dotyczące pola powierzchni oraz objętości kuli, czaszy kulistej, walca oraz objętości paraboloidy, elipsoidy i hiperboloidy obrotowej. Oszacował również poprawnie wartość pi i nazwał od pierwszej litery wyrazu greckiego "perimetros" co oznacza obwód koła. Również on wynalazł wielokrążek udoskonalony oraz tak zwaną śrubę Archimedesa. Konstruował machiny wojenne, które były wykorzystywane do obrony przed Rzymianami Syrakruz w latach 214-212 p. n. e., co miało miejsce podczas II wojny punickiej. Po zdobyciu miasta został zabity przez żołnierza rzymskiego.
Euklides z Aleksandrii (ok. 365 - ok. 300 p. n. e.)
Jest autorem obowiązującego przez stulecia podręcznika "Elementy geometrii". Usystematyzował on całość starej wiedzy matematycznej. Sformułował w swoich pracach z optyki prawo załamania oraz zasadę prostoliniowego rozchodzenia się światła. Pisał również dzieła z teorii muzyki oraz z astronomii.
François Viete (1540-1603)
Z zawodu prawnik oraz autor prac z trygonometrii sferycznej oraz algebry. Wprowadził oznaczenia literowe dla stałych w równaniach oraz opracował metody rozwiązywania równań drugiego, trzeciego i czwartego stopnia. Jego imieniem są nazwane również wzory, które wiążą współczynniki równania z jego pierwiastkami.


