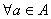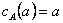Zdania logiczne
Zaprzeczenie zdania p to zdanie "nieprawda że p" - oznaczenie "~p"
Koniunkcja jest fałszywa gdy co najmniej jedno zdanie jest fałszywe.
Alternatywa jest fałszywa gdy co najmniej jedno zdanie jest prawdziwe.
Implikacja jest fałszywa gdy poprzednik jest prawdziwy a następnik fałszywy.
Równoważność jest fałszywa gdy oba zdania mają te samą wartość logiczną.
Prawa logiczne
Prawo logiczne - zdanie w logice, które zawsze ma wartość 1.
zasada wyłączonego środka: 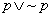
zasada sprzeczności: 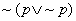
podwójne przeczenie: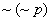
łączność alternatyw: 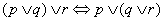
łączność koniunkcji: 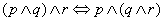
przemienność alternatywy: 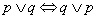
przemienność koniunkcji: 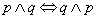
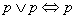
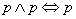
eliminacja implikacji: 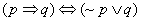 ,
,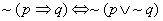
przechodniość implikacji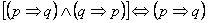
prawo rozdzielności koniunkcji względem alternatywy: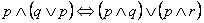
prawo rozdzielności alternatywy względem koniunkcji: 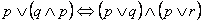
Prawa De Morgana:
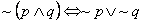
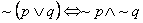
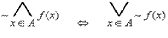


Definicje zbiorów :
- Część wspólna zbiorów (iloczyn zbiorów):
![]()
- Suma zbiorów:
![]()
- Różnica zbiorów:
![]()
- Iloczyn kartezjański zbiorów A i B to taki zbiór par uporządkowanych, że pierwszy element pary należy do A, a drugi do B
-
![]()
- Para uporządkowana: ważna jest kolejność, (a, b) para uporządkowana, gdy jeden z elementów jest wyróżniony jako pierwszy.
-
![]() jest relacją zwrotną
jest relacją zwrotną ![]()
![]()
-
![]() jest relacją symetryczną
jest relacją symetryczną ![]()
![]()
-
![]() jest relacją przechodnią
jest relacją przechodnią ![]()
![]()
-
![]() jest relacją asymetryczną
jest relacją asymetryczną ![]()
![]()
-
![]() jest relacją spójną
jest relacją spójną ![]()
![]()
- Relacja R określona w zbiorze A jest relacją równoważności
![]() jest zwrotna, symetryczna oraz przechodnia.
jest zwrotna, symetryczna oraz przechodnia. - Relacja R określona w zbiorze A jest relacją częściowego porządku
![]() jest zwrotna, asymetryczna oraz przechodnia.
jest zwrotna, asymetryczna oraz przechodnia. - Relacja R określona w zbiorze A jest relacją porządku
![]() jest zwrotna, asymetryczna, przechodnia oraz spójna.
jest zwrotna, asymetryczna, przechodnia oraz spójna. - Zbiorem częściowo uporządkowanymnazywamy parę
![]() gdzie A jest zbiorem, a R jest relacją częściowego porządku określoną na zbiorze A.
gdzie A jest zbiorem, a R jest relacją częściowego porządku określoną na zbiorze A. - Zbiorem uporządkowanymnazywamy parę
![]() gdzie A jest zbiorem, a R jest relacją porządku określoną na zbiorze A.
gdzie A jest zbiorem, a R jest relacją porządku określoną na zbiorze A. - Element
![]() nazywamy elementem min lub max w zbiorze
nazywamy elementem min lub max w zbiorze ![]()
![]()
![]() ,
,![]()
Definicje odwzorowań:
- Przeciwobrazem elementu
![]() poprzez odwzorowanie
poprzez odwzorowanie ![]() jest zbiór =
jest zbiór =![]() ,
, ![]()
- Przeciwobrazem zbioru
![]() poprzez odwzorowanie
poprzez odwzorowanie ![]() jest zbiór =
jest zbiór =![]() ,
, ![]()
- Surjekcja, odwzorowanie zbioru A na zbiór B - takie, że każdy element zbioru B przyporządkowany jest co najmniej jednemu elementowi zbioru A.
- Odwzorowanie
![]() nazywamy odwzorowaniem surjektywnym (suriekcją):
nazywamy odwzorowaniem surjektywnym (suriekcją):
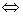
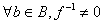 ,
, 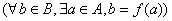
- Iniekcja relacja przyporządkowująca jednemu elementowi zbioru A jeden i tylko jeden element zbioru B.
- Odwzorowanie
![]() nazywamy odwzorowaniem iniektywnym (iniekcja):
nazywamy odwzorowaniem iniektywnym (iniekcja): -
![]()
![]()
- Bijekcja, matematyczna relacja pomiędzy zbiorami A i B taka, że każdemu elementowi zbioru A przyporządkowany jest dokładnie jeden element zbioru B i wzajemnie: każdemu elementowi zbioru B przyporządkowany jest dokładnie jeden element zbioru A. B. jest suriekcją i jednocześnie iniekcją.
- odwzorowanie
![]() nazywamy odwzorowaniem biekcyjnym
nazywamy odwzorowaniem biekcyjnym ![]() jest surjekcją oraz iniekcją
jest surjekcją oraz iniekcją - odwzorowanie identycznosciowe
![]() ,
, ![]()
![]()

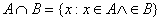
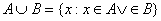
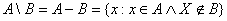
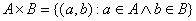
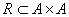 jest relacją zwrotną
jest relacją zwrotną 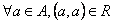
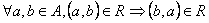
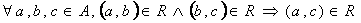
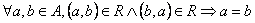
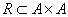 jest relacją spójną
jest relacją spójną 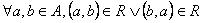
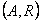 gdzie A jest zbiorem, a R jest relacją częściowego porządku określoną na zbiorze A.
gdzie A jest zbiorem, a R jest relacją częściowego porządku określoną na zbiorze A.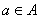 nazywamy elementem min lub max w zbiorze
nazywamy elementem min lub max w zbiorze 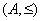
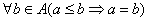 ,
,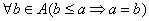
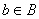 poprzez odwzorowanie
poprzez odwzorowanie 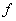 jest zbiór =
jest zbiór =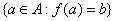 ,
, 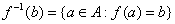
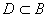 poprzez odwzorowanie
poprzez odwzorowanie 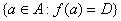 ,
, 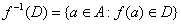
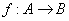 nazywamy odwzorowaniem surjektywnym (suriekcją):
nazywamy odwzorowaniem surjektywnym (suriekcją):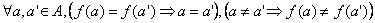
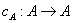 ,
,