Podstawowym pojęciem matematyki jest liczba. Człowiek był ich świadomy niemal od początku swego istnienia. W miarę rozwoju kultury i cywilizacji zaczęto rozróżniać jedności od wielości, które były charakterystyczne ludom pierwotnym. Wprowadzono liczby naturalne: 1,2,3,4,..., które są całkowite i dodatnie. Ich zaznaczanie odbywało się poprzez nacinanie zwierzęcych kości lub innych kijów, czy przedmiotów. Gdy zaczęło się rozwijać pismo powstały systemy zapisania liczb przy pomocy znaków. W czasach Euklidesa i Archimedesa zauważono, że proces tworzenia kolejnych liczb jest nieskończony. Archimedes opracował metodę, która pozwalała zapisywać i nazywać liczby większe niż "liczba ziaren piasku na świecie".
Arytmetyka została zapoczątkowana gdy określono zasady dodawania, odejmowania, dzielenia i mnożenia oraz gdy określono ich własności.
Pojęcie liczb rozszerzono, gdy wprowadzono ułamki, dzięki nim potrafiono już dzielić liczby naturalne.
Kolejnym etapem było wprowadzenie liczb ujemnych oraz zera, co miało miejsce w Indiach w VI - XI w.
Kolejną innowacją było wprowadzenie przez Descartesa wektorów jako interpretacji odcinka łączącego 2 punkty z wyróżnionym na nim kierunkiem. Początek wektora to jeden punkt, natomiast jego koniec to drugi punkt, przy czym wektor jest skierowany w stronę przeciwną niż kierunek osi liczbowej. W głównej mierze dzięki Descartesowi w Europie rozpowszechniły się liczby ujemne.
Kolejnym postępem, było rozróżnienie liczb dodatnich od ujemnych oraz wyróżnienie liczb wymiernych jako ułamków, w których licznik jest liczbą całkowitą, a mianownik naturalną. Liczby wymierne są zbiorem gęstym, co oznaczam że mając dwie dowolne liczby wymierne, możemy znaleźć trzecią, która leży pomiędzy nimi. Następne poszerzenie pojęcia liczb to liczby niewymierne, czyli takie które nie dają się przedstawić w takich ułamkach jak wymierne. Najlepszym przykładem może być tutaj pierwiastek z trzech. Na liczby rzeczywiste składają się wszystkie liczby wymierne oraz niewymierne.
Najbardziej zaawansowane było wprowadzenie liczb zespolonych, którymi są pary liczb rzeczywistych, w których ważny jest porządek występowania. Na liczbach zespolonych można wykonywać działania dodawania i mnożenia, które są dla nich specjalnie zdefiniowane. Liczbami zespolonymi są również liczby rzeczywiste, ale mają one zerową część urojoną, czyli drugą liczbę z pary.
Babilończycy zauważyli, że wszystko w przyrodzie i na niebie jest cykliczne. Dzień następuje po nocy, noc po dniu, pory roku pojawiają się w ustalonym porządku, tak jak fazy księżyca. Uznali oni, że liczby są wyrażeniem kosmicznego porządku.
Symboliczne znaczenie liczb przejawia się w wielu kulturach. Ludzie zajmujący się numerologią badają jak wpływają one na naszą przyszłość. Liczby wyrażają nie tylko stosunki ilościowe ale również jakościowe. Przykładem może być liczba siedem, uznawana za świętą, ponieważ przedstawia jedność ziemi (4) z pierwiastkiem boskim (3).
Poniżej został przedstawiony graf podziału liczb:
Liczby zespolone
 |  |
Liczby rzeczywiste liczby nierzeczywiste
 |  |
Liczby niewymierne liczby wymierne
 |  |

 Liczby całkowite liczby niecałkowite
Liczby całkowite liczby niecałkowite
(dodatnie i ujemne)
liczby naturalne zero liczby całkowite ujemne
1. Liczby rzeczywiste są liczbami, którym odpowiadają punkty na osi liczbowej.
2. Liczby wymierne są to liczby, które dają się przedstawić za pomocą zwykłego ułamka 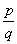 , w którym p to dowolna liczba całkowita, natomiast q to dowolna liczba naturalna.
, w którym p to dowolna liczba całkowita, natomiast q to dowolna liczba naturalna.
3. Liczby niewymierne są to liczby, które nie dają się przedstawić w postaci zwykłego ułamka.
4. Liczby rzeczywiste to liczby wymierne i liczby niewymierne.
5. Liczby naturalne to liczby, które są dodatnie i są całościami. Są one jednocześnie rzeczywiste i wymierne.
6. Liczby całkowite są całościami, należą tu liczby dodatnie oraz przeciwne do nich. Są one rzeczywiste i wymierne.
7. Liczby pierwsze to takie, które mają dwa dzielniki 1 oraz samą siebie
8. Liczby złożone to takie liczby, które mają więcej niż dwa dzielniki


