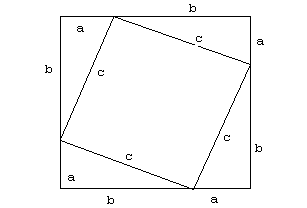
Niech a i b będą przeciwprostokątnymi trójkąta, c zaś - przyprostokątną. Ustawmy cztery kopie tego trójkąta tak, by przylegały do siebie jak na rysunku. Przyprostokątne tych trójkątów utworzą one kwadrat o boku (a+b), a przeciwprostokątne - kwadrat o boku c.
Pole dużego kwadratu wynosi (a+b)^2=a^2+2ab+b^2. Ale to samo pole można obliczyć sumując pola czterech trójkątów i kwadratu o boku c. Jest ono zatem równe 4*((1/2)*a*b)+c^2=2ab+c^2.
Mamy zatem a^2+2ab+b^2=2ab+c^2, czyli a^2+b^2=c^2. Udowodniliśmy więc twierdzenie Pitagorasa.


