Funkcja wymierna to funkcja postaci W/V, gdzie W oraz V są wielomianami. Dziedziną funkcji wymiernej W/V jest zbiór liczb rzeczywistych pomniejszony o zbiór zer wielomianu V (bo przez zero nie wolno dzielić).
Przykład: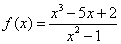 
Dziedziną tej funkcji jest zbiór R {-1,1}.
Suma dwóch lub skończonej ilości funkcji wymiernych też jest funkcją wymierną.
Równanie postaci W/V=C, gdzie C jest stałą, wielomianem lub funkcją wymierną nazywamy wymiernym, gdy wyrażenie W/V jest funkcją wymierną. Równanie takie zawsze można sprowadzić do równania postaci W'/V'=0 przenosząc C na lewą stronę i sprowadzając lewą stronę do wspólnego mianownika.
Aby rozwiązać równanie wymierne należy przemnożyć obie jego strony przez taki wielomian, że po przemnożeniu otrzymamy równanie algebraiczne.
Przykład. Rozwiązać równanie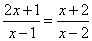 
.
Rozwiązanie. Określamy dziedzinę: jest nią zbiór liczb rzeczywistych bez 1 oraz 2. Obie strony mnożymy przez wielomian (x-1)(x-2) i otrzymujemy: (2x+1)(x-2)=(x-1)(x+2). Po wymnożeniu oraz zredukowaniu i przeniesieniu wyrazów na lewą stronę otrzymujemy:
x^2-4x=0. Jest to zwykłe równanie kwadratowe, jego pierwiastki to 0 i 4. Ponieważ równanie to jest równoważne równaniu wyjściowemu, zatem 0 i 4 są pierwiastkami tego równania.
UWAGA! Należy zawsze sprawdzić, czy liczby spełniające równanie należą do dziedziny funkcji wymiernych tworzących równanie wymierne.
Funkcja wykładnicza
Funkcja wykładnicza to funkcja postaci f(x)=a^x, gdzie a>0. Stała a nazywana jest podstawą funkcji wykładniczej.
Własności funkcji wykładniczej:
Funkcja wykładnicza jest rosnąca gdy a>1
Funkcja wykładnicza jest malejąca, gdy 0 Funkcja wykładnicza jest stała i równa 1, gdy a=1 Funkcja wykładnicza jest ciągła Funkcja wykładnicza jest zawsze dodatnia, dla każdego x Dla a różnego od 1 funkcja wykładnicza a^x jest monotoniczna. Wynika z tego, że jeśli liczba a spełnia ten warunek, to dla każdych liczb x i y spełniona jest implikacja: a^x=a^y => x=y Funkcja logarytmiczna Niech a>0 i a różne od jeden. Funkcja logarytmiczna o podstawie a to funkcja (*) Funkcja log_a(x) przyjmuje wartość y wtedy i tylko wtedy, gdy a^y=x. Własności funkcji logarytmicznej Funkcja logarytmiczna jest rosnąca dla a>1 Funkcja logarytmiczna jest malejąca dla 0 Funkcja logarytmiczna jest ciągła w każdym punkcie dziedziny Funkcja logarytmiczna log_a(x) jest odwrotna do funkcji wykładniczej a^x Dwie pierwsze własności gwarantują różnowartościowość funkcji logarytmicznej. Wynika z tego więc następująca własność: Włansości funkcji logarytmicznej (wynikają z definicji (*) ) log_a(x1*x2)=log_a(x1)+log_a(x2) - logarytm iloczynu jest równy sumie logarytmów log_a(x1/x2)=log_a(x1)-log_a(x2) - logarytm ilorazu jest równy różnicy logarytmów log_a(x^t)=t*log_a(x) Wielomiany Wielomian n-tego stopnia jednej zmiennej to funkcja postaci a0, a1,..., an to współczynniki wielomianu. Współczynnik a0 nazywany jest wyrazem wolnym. Wielomian jest takiego stopnia, jaka jest najwyższa niezerowa potęga zmiennej x. W(x)=0 to wielomian zerowy. W(x)=c, gdzie c jest stałą - to wielomian stopnia zerowego W(x)=a+bx - to wielomian stopnia pierwszego itd. Wielomian stopnia pierwszego to funkcja liniowa. Wielomian stopnia drugiego to funkcja kwadratowa. Suma R dwóch wielomianów P i Q jest również wielomianem. W nowym wielomianie R współczynnik stojący przy n-tej potędze jest sumą współczynników stojących przy zmiennej w n-tej potędze wielomianów P i Q. Analogicznie różnica dwóch wielomianów jest też wielomianem. Tym razem współczynnik przy n-tej potędze jest różnicą odpowiednich współczynników w wielomianach P i Q. Iloraz dwóch wielomianów nie zawsze jest wielomianem. Twierdzenie Bezouta. Wielomian W(x) dzieli się bez reszty przez dwumian (x-a) wtedy i tylko wtedy, gdy W(a)=0. Jeżeli wielomian W(x) dzieli się przez x-a to a jest pierwiastkiem wielomianu W. Twierdzenie o reszcie Reszta z dzielenia wielomianu W(x) przez (x-a) równa jest wartości wielomianu dla x=a, czyli równa jest W(a). Miejsca zerowe wielomianów. Zasadnicze twierdzenie algebry mówi, że wielomian stopnia n ma dokładnie n pierwiastków, jednak nie wszystkie z nich muszą być liczbami rzeczywistymi (zwykle są liczbami zespolonymi). Aby znaleźć pierwiastki wielomianów można posłużyć się jedną z dwóch metod: 1. Spróbować rozłożyć wielomian na czynniki 2. Spróbować znaleźć pierwiastek na "chybił trafił" Jeśli istnieją wymierne pierwiastki wielomianu W(x) to są one postaci p/q, gdzie p jest podzielnikiem wyrazu wolnego, czyli a0, a q jest podzielnikiem współczynnika a_n, gdzie n jest stopniem wielomianu. W metodzie tej można posługiwać się tzw. tabelą Hornera: w pierwszej kolumnie tabeli wypisujemy kandydata na pierwiastek, czyli liczbę p/q. W każdej następnej kolumnie wypisujemy wartości t1, t2, ... aż do tn, gdzie n jest stopniem wielomianu, t1=a1, t_i=(p/q)*t_{i-1}+a_{i-1}. Gdy dojedziemy do wartości t_n i będzie ona równa zero, oznacza to, że p/q jest szukanym pierwiastkiem wielomianu W. Podczas obliczania kolejnych wartości należy uwzględniać także te a_i, które są równe zero i nie opuszczać ich. Jeśli znajdziemy pierwiastek x0, to wielomian ma postać: W(x)=(x-x0)*P(x) gdzie P(x)= t1*x^{n-1} + t2*x^{n-2} + ... + t_{n-1} Po znalezieniu x0 możemy znów szukać kolejnego pierwiastka, tym razem już w wielomianie P(x). Funkcje potęgowe. Funkcja potęgowa to funkcja postaci x^a, gdzie a jest dowolną liczbą rzeczywistą. Dziedziną funkcji potęgowej jest zbiór liczb rzeczywistych. Gdy a jest liczbą naturalną, to a. jeśli jest liczbą parzystą, to funkcja potęgowa jest malejąca na przedziale (-∞,0] i rosnąca na przedziale [0,∞). b. jeśli jest liczbą nieparzystą, to funkcja potęgowa jest rosnąca na całej dziedzinie. Gdy a jest liczbą całkowitą dodatnią, to funkcja potęgowa x^{-2a} jest określona na zbiorze R {0}. Jest monotonicznie rosnąca na (-∞,0) i monotonicznie malejąca na (0,∞). Dla a=0 przyjmujemy z definicji x^a := 1 dla x różnych od 0. Wyrażenie 0^0 jest nieokreślone. Parę własności funkcji potęgowych: x^a * x^b = x^(a+b) (x^p)^q = x^(p*q) Funkcje trygonometryczne Sinus (sin) kąta Cosinus (cos) kąta Tangens (tg) kąta Cotangens (ctg) kąta Własności funkcji trygonometrycznych: sin2( tg( ctg( tg( Znaki funkcji trygonometrycznych w kolejnych ćwiartkach Wierszyk ułatwiający zapamiętanie: "w pierwszej wszystkie są dodatnie, w drugiej tylko sinus / w trzeciej tangens i kotangens, a w czwartej cosinus". 1 2 3 4 sin x + + - - cos x + - - + tg x + - + - ctg x + - + - Funkcje trygonometryczne sum i różnic kątów oraz wielokrotności kątów sin(x+y)=sin(x)*cos(y)+cos(x)*sin(y) sin(x-y)=sin(x)*cos(y)-cos(x)*sin(y) cos(x+y)=cos(x)*cos(y)-sin(x)*sin(y) cos(x-y)=cos(x)*cos(y)+sin(x)*sin(y) tg(x+y)=(tg(x)+tg(y))/(1-tg(x)tg(y)) tg(x-y)=(tg(x)-tg(y))/(1+tg(x)*tg(y)) ctg(x-y)=(ctg(x)*ctg(y)+1)/(ctg(x)-ctg(y)) ctg(x+y)=(ctg(x)*ctg(y)-1)/(ctg(x)+ctg(y)) sin(2x)=2sin(x)cos(x) cos(2x)=cos^2(x)-sin^2(x) Zamiana sum i różnic funkcji trygonometrycznych na iloczyn Funkcje cyklometryczne Funkcje cyklometryczne to funkcje odwrotne do funkcji trygonometrycznych, określone na zbiorze będącym zbiorem wartości danej funkcji trygonometrycznej określonej na zbiorze na którym jest różnowartościowa. Funkcją odwrotną do funkcji sin(x) w przedziale, w którym jest różnowartościowa jest funkcja arcsin(x) Funkcją odwrotną do funkcji cos(x) w przedziale, w którym jest różnowartościowa jest funkcja arccos(x) Funkcją odwrotną do funkcji tg(x) w przedziale, w którym jest różnowartościowa jest funkcja arctg(x). Dziedziną są liczby rzeczywiste. arctg(x)=y <=> tg(y)=x Funkcją odwrotną do funkcji ctg(x) w przedziale, w którym jest różnowartościowa jest funkcja arctg(x). Dziedziną są liczby rzeczywiste. arcctg(x)=y <=> ctg(y)=x Funkcja homograficzna to funkcja wymierna postaci f(x)=(ax+b)/(cx+d), gdzie c jest różne od zera, a,b,c,d są ustalonymi stałymi, x jest zmienną. Ponadto zakłada się, że a*d-b*c musi być różne od zera, bo w przeciwnym razie licznik i mianownik zawierałyby w sobie tę samą funkcję liniową, zatem można było by skrócić to wyrażenie i otrzymać funkcję stałą. Dziedziną funkcji homograficznej jest zbiór R z wyłączeniem miejsca zerowego mianownika, czyli zbiór R {-d/c}. Przeciwdziedziną jest zbiór R {a/c}. Miejsce zerowe: x0=-b/a jeśli a jest różne od zera. Gdy a jest różne od zera, funkcja nie posiada miejsca zerowego. Wykresem funkcji homograficznej (ax+b)/(cx+d) jest hiperbola posiadająca dwie asymptoty: poziomą y=a/c, oraz pionową y=-d/c. Najprostszą funkcją homograficzną jest funkcja f(x)=1/x.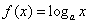 
. Dziedziną takiej funkcji logarytmicznej jest zbiór liczb rzeczywistych dodatnich.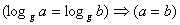
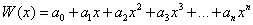
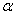to stosunek rzędnej dowolnego punktu leżącego na końcowym ramieniu kąta do promienia wodzącego tego punktu. 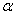to stosunek odciętej dowolnego punktu leżącego na końcowym ramieniu kąta do promienia wodzącego tego punktu. 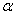to stosunek rzędnej dowolnego punktu leżącego na końcowym ramieniu kąta do odciętej tego punktu. 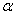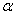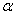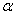to stosunek odciętej dowolnego punktu leżącego na końcowym ramieniu kąta do rzędnej tego punktu.)+cos2()=1)=sin(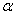)/cos(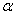), 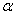różne od (pi/2)+k*pi, k całkowite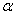)=cos(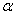)/sin(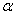), 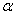różne od k*pi, k całkowite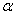)*ctg(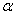)=1, 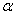różne od k*(pi/2), k całkowite
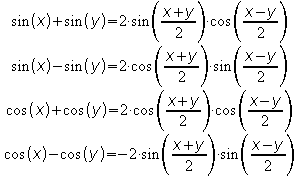
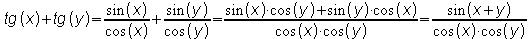
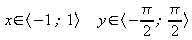. arcsin(x)=y <=> sin(y)=x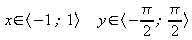. arccos(x)=y <=> cos(y)=x
