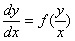RÓWNANIA RÓŻNICZKOWE JEDNORODNE WZGLĘDEM X i Y

 stosujemy podstawienie  ==>

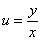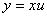
różniczkujemy 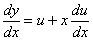 podstawiamy do równania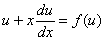

RÓWNANIA RÓŻNICZKOWE TYPU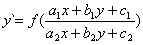

Przypadek I : a₁b₂ - b₁a₂ ¹ 0

Układ równań posiada jedno rozwiązanie x=a i y=b

Wprowadzamy zamianę zmiennych: x - a = u; y - b = v

W efekcie dostaniemy przekształcone równanie różniczkowe: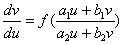

Podstawiamy  =>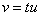  

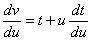
Stasujemy metodę rozdzielania zmiennych i całkujemy.

Przypadek II : a₁b₂ - b₁a₂ = 0

Współczynnik proporcjonalności :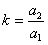 

Wprowadzamy zmienną : 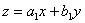 => po różniczce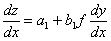

Uwzględniając wzory równanie ma postać :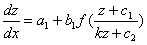 

Stosujemy metodę rozdzielania zmiennych.

RÓWNANIA RÓŻNICZKOWE LINIOWE NIEJEDNORODNE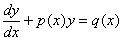

Stosujemy w tym przypadku metodę "uzmienniania stałej"

Po pierwsze rozwiązujemy równanie jednorodne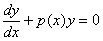

Całką powyższego równania jest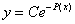

Stałą C zamieniamy na funkcję 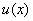i otrzymujemy: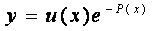

Obliczamy pochodną : 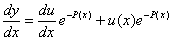 podstawiamy, przeprowadzamy redukcję i liczymy

PRZYKŁAD :

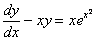
Rozwiązujemy równanie jednorodne 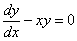 (metoda rozdzielania zmiennych)

Otrzymujemy 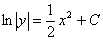 gdzie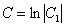

Likwidujemy logarytmy, otrzymujemy: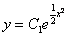

Uzmiennianie stałej C₁ :  (**)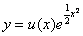

Obliczamy pochodną :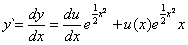 

Obliczone wartości y i y` podstawiamy do pierwszego równania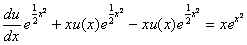

Po zredukowaniu otrzymamy 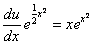czyli

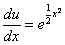
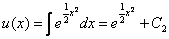 to wstawiamy do równania (**) i otrzymujemy końcowy wynik

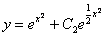
RÓWNANIA RÓŻNICZKOWE TYPU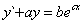

Przewidzenie : y₁ = me^Cx lub y₁ = (mx+n)e^Cx

PRZYKŁAD

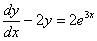
Przewidujemy :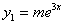 

Obliczamy z powyższego pochodną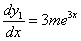

Wartośc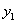i i 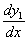wstawiamy do równania pierwszego :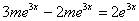 

Po uproszczeniu (dzielimy przez e^3x) znajdujemy m = 2

Podstawiamy m do równania na 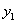, dostaniemy: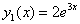

Obliczamy całkę ogólną naszego równania uproszczonego :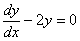 

Po rozwiązaniu otrzymujemy: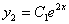

Ogólna całka całego równania wynosi y₁+y_2, czyli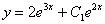

RÓWNANIA RÓŻNICZKOWE TYPU ,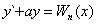

gdzie a jest liczbą stałą, a W_n(x) jest wielomianem stopnia n

PRZYKŁAD:

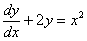
Przewidzenie :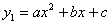  

Obliczamy pochodną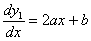

Podstawiamy te wartości do równania pierwszego: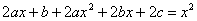

Przyrównujemy współczynniki występujące przy takich samych potęgach przy zmiennej x, stąd otrzymujemy związki:

2a=1; 2a+2b=0; b+2c=0; stąd mamy :

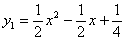
Rozwiązujemy równanie jednorodne 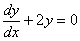 i stąd mamy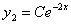

Ogólna całka ma postać y₁ + y₂, czyli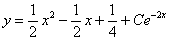

RÓWNANIA RÓŻNICZKOWE TYPU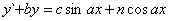

Przewidzenie :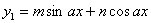 

PRZYKŁAD

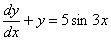
Przewidujemy :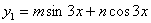 

Obliczamy pochodną z powyższego: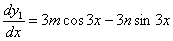

Podstawiamy do równości pierwszej :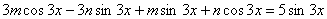 

Wyliczamy n i m, otrzymujemy: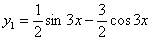

Rozwiązujemy równanie jednorodne 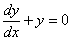 stąd mamy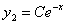

Całka ogólna jest postaci :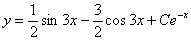 

RÓWNANIA RÓŻNICZKOWE INNYCH TYPÓW

PRZYKŁAD 1

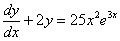
PRZEWIDZENIE :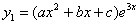 

Obliczamy pochodną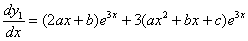

Podstawiamy do pierwszego równania oraz dzielimy przez e^3x,

Otrzymujemy :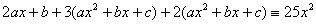 

Wyliczamy a,b,c i stąd mamy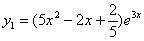

Obliczamy ogólną całkę równania jednorodnego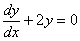  i dostajemy ostatecznie

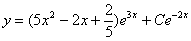
PRZYKŁAD 2

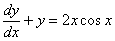
PRZEWIDUJEMY :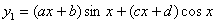 

Liczymy pochodną :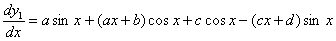 

Podstawiamy do pierwszego równania, otrzymujemy równanie,

obliczamy współczynniki

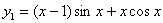
Liczymy ogólną całkę równania jednorodnego,

ostatecznie mamy :

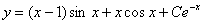
RÓWNANIA RÓŻNICZKOWE RZĘDU DRUGIEGO

TYP :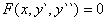 

Podstawienie :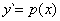 

PRZYKŁAD

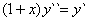
Stosujemy podstawienie : 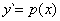 otrzymujemy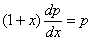

Rozdzielamy zmienne 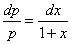 mamy ln p = ln (1+x) +ln C, wiec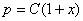  

to znaczy 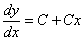 czyli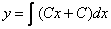

ostatecznie otrzymujemy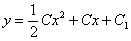

TYP :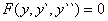 

Podstawienie :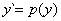 

wówczas 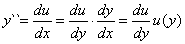, równanie zostanie przekształcone w równanie pierwszego rzędu.