Proste prostopadłe w przestrzeni
Proste, które są prostopadłe na płaszczyźnie przecinają się w jednym punkcie i każda z nich jest dla drugiej jej osią symetrii.
Takie proste prostopadłe na płaszczyźnie, są również prostopadłe w przestrzeni. Zajmiemy się teraz rozszerzeniem pojęcia prostopadłości dla prostych prostopadłych w przestrzeni, co będzie obejmowało proste skośne. Będziemy tutaj używali pojęcia wektorów prostopadłych. Pojęcie wektorów prostopadłych na płaszczyźnie można w sposób analogiczny przenieść na pojęcie wektorów prostopadłych w przestrzeni.
Definicja:
Dwie proste są prostopadłe wtedy i tylko wtedy gdy niezerowy wektor równoległy do jednej z prostych i niezerowy wektor równoległy do drugiej prostej, są prostopadłe.
Przykład 1:
Prosta, która jest równoległa do krawędzi bocznej pewnego prostopadłościanu jest jednocześnie prostopadła do wszystkich prostych równoległych do krawędzi dowolnej podstawy.
Prosta i płaszczyzna - prostopadłość
Spróbujmy sobie wyobrazić taką sytuację: mamy dane 2 płaszczyzny: q i r, które przecinają się wzdłuż prostej k.
Ustalmy na prostej k w dowolnym miejscu punkt O. Przez ten punkt przeprowadzamy prostą, która jest prostopadła do prostej k i leży w płaszczyźnie q, nazwijmy tą prostą a. Drugą prostą poprowadzimy również prostopadle do prostej k, ale będzie leżała w płaszczyźnie r, nazwiemy ją b. Tak wyznaczone proste przecinają się w punkcie O, więc wyznaczają nam płaszczyznę, nazwijmy ją p. Tak więc prosta k leży prostopadle do 2 prostych, które się przecinają i są zawarte w płaszczyźnie p. Obrazuje to poniższy rysunek.

Twierdzenie:
Jeżeli mamy daną prostą, która jest prostopadła do 2 prostych a i b, które się przecinają, to prosta k jest prostą prostopadłą do wszystkich prostych, które są zawarte w płaszczyźnie wyznaczonej prostymi a i b.
Dowód:
Posługując się definicją prostopadłości wiemy, że prosta k jest prostą prostopadłą do dowolnej prostej, która jest równoległa do prostej a lub prostej b.
Wystarczy wykazać, że prosta k jest prostą prostopadłą do dowolnej trzeciej prostej, która jest zawarta w płaszczyźnie p nie jest równoległa ani do a ani do b. Weźmy prostą c, która przechodzi przez O.
Oznaczmy przez OA, OB, OC i OK wektory odpowiednio równoległe do prostych a, b, c i k.
Wiemy, że punkty O, A, B i C leżą w płaszczyźnie p oraz, że punkty A, B, O są punktami niewspółliniowymi, stąd istnieją liczby x i y takie, że:
OC = x * OA + y * OB
Na podstawie własności iloczynu skalarnego wektorów będziemy mieli:
OK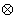 OC = (x * OA + y * OB)
OC = (x * OA + y * OB) 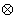 OK = x * (OK
OK = x * (OK 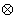 OA) + y * (OK
OA) + y * (OK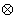 OB)
OB)
Z założeń twierdzenia mamy, że wektor OK jest prostopadły do wektorów OA i OB, stąd:
OK. 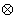 OA = 0 i OK
OA = 0 i OK 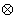 OB = 0
OB = 0
Stąd otrzymujemy:
OK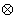 OC = x * 0 + y * 0 = 0,
OC = x * 0 + y * 0 = 0,
co znaczy, że wektor OK jest prostopadły do wektora OC czyli, że prosta k jest prostopadła do prostej c.
W ten sposób pokazaliśmy, że 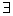 prosta, która leży prostopadle do wszystkich prostych, zawartych w płaszczyźnie. Jednocześnie jest ona prostopadła do wszystkich prostych równoległych do tej płaszczyzny.
prosta, która leży prostopadle do wszystkich prostych, zawartych w płaszczyźnie. Jednocześnie jest ona prostopadła do wszystkich prostych równoległych do tej płaszczyzny.
Prosta jest prostopadła do płaszczyzny wtedy, gdy jest ona prostopadła do wszystkich prostych zawartych w płaszczyźnie.
Wektor jest prostopadły do płaszczyzny wtedy, gdy jest on równoległy do prostej, która jest prostopadła do płaszczyzny.


