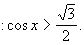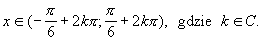Równanie trygonometryczne to równanie, dla którego niewiadoma znajduje się w argumentach pochodzących z funkcji trygonometrycznych.
Przy rozwiązywaniu równanie trygonometrycznego należy znaleźć każdy pierwiastek tego równania.
Poniżej zostaną przedstawione rozwiązania elementarnych równań trygonometrycznych.
1. Równanie 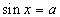 posiada rozwiązanie wtedy i tylko wtedy gdy
posiada rozwiązanie wtedy i tylko wtedy gdy 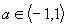 wtedy:
wtedy:
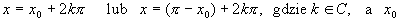 jest to rozwiązanie należące do
jest to rozwiązanie należące do
przedziału 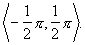
Przykład:
Rozwiązać równanie: 
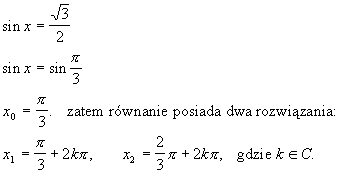
2.Równanie  posiada rozwiązanie wtedy i tylko wtedy, gdy
posiada rozwiązanie wtedy i tylko wtedy, gdy 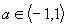 wtedy:
wtedy:
 jest to rozwiązanie należące do
jest to rozwiązanie należące do
przedziału 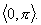
Przykład:
Rozwiązać równanie: 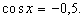
Korzystamy ze wzoru redukcyjnego, otrzymujemy:
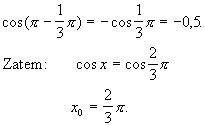
Równanie ma dwa rozwiązania:
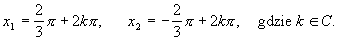
3. Równanie 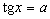 posiada dla każdego
posiada dla każdego 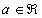 rozwiązanie, które jest opisane wzorem:
rozwiązanie, które jest opisane wzorem:
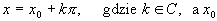 jest to rozwiązanie należące do
jest to rozwiązanie należące do
przedziału: 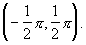
Przykład:
Rozwiązać równanie: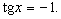

Rozwiązaniem tego równania jest: 
4. Równanie 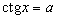 posiada dla każdego
posiada dla każdego 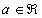 rozwiązanie, które jest opisane wzorem:
rozwiązanie, które jest opisane wzorem:
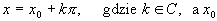 jest to rozwiązanie należące do
jest to rozwiązanie należące do
przedziału: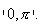
Przykład:
Rozwiązać równanie: 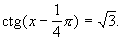
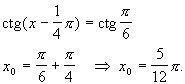
Równanie ma rozwiązanie: 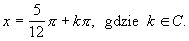
Jeżeli w równaniu trygonometrycznym występuje jedna funkcja trygonometryczna oraz tylko jeden argument, możemy go rozwiązać za pomocą wprowadzonej pomocniczej niewiadomej, przez co doprowadzamy do jednego albo kilku elementarnych równań.
Jeżeli w równaniu trygonometrycznym występuje tylko jeden argument oraz różne funkcje trygonometryczne, możemy go rozwiązać przekształcając przy pomocy związków występujących pomiędzy funkcjami trygonometrycznymi dla takiego samego argumentu oraz sprowadzamy do równania, które zawiera jedną funkcję oraz jeden argument.
Przykład:
Rozwiązać równanie: 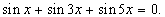
Korzystamy ze wzoru: suma funkcji trygonometrycznych, dodajemy: 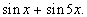
Mamy zatem:
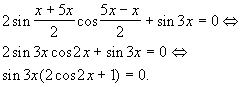
stąd: 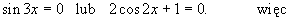
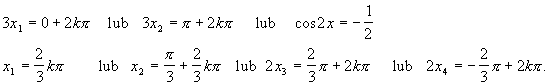
Równanie to ma cztery rozwiązania:
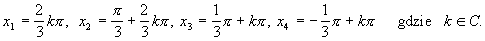
Nierówność trygonometryczna to nierówność, dla której niewiadoma znajduje się w argumentach pochodzących z funkcji trygonometrycznych.
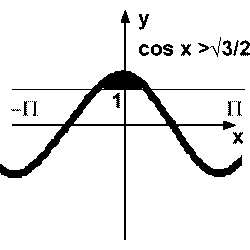
Gdy rozwiązujemy nierówność, stosujemy wskazówki z wykresów dla funkcji trygonometrycznych. Inne przekształcenia są wykonywane tak jak dla zwykłych równań.
Przykład:
Rozwiązać nierówność