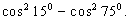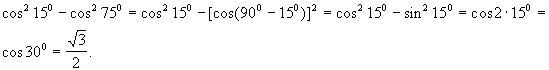Tożsamością dwóch wyrażeń nazywamy równość 2 wyrażeń, zachodzącą dla każdej wartości zmiennych, które w nim występują.

Przykład: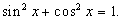

Jeżeli równość 2 wyrażeń prawdziwa jest dla każdej wartości zmiennych ale pod pewnym warunkiem, nazywamy ją tożsamością warunkową.

Przykład:

Jeżeli: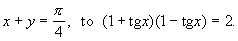

Aby rozstrzygnąć, czy tożsamość jest prawdziwa, należy doprowadzić obie strony lub jedną z nich do takiej samej postaci.

Przykład:

Udowodnić tożsamość:

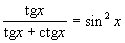
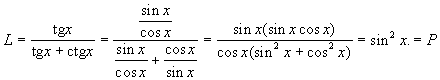
Funkcje trygonometryczne dla sumy oraz różnicy argumentu.

Twierdzenie:

Dla dowolnych x i y - liczb rzeczywistych prawdziwe są następujące wzory:

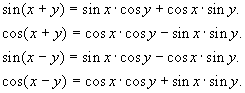
Twierdzenie:

Niech x, y takie liczby rzeczywiste, że:

1. 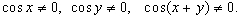Wówczas:

2.

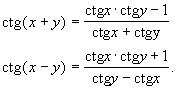
Funkcje trygonometryczne dla podwojonego argumentu

Twierdzenie:

Następujące wzory są prawdziwe:

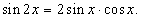 dla każdego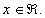

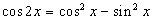 dla każdego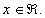

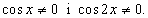
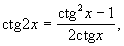gdy

gdy

Sumy oraz różnice dla funkcji trygonometrycznych

Twierdzenie:

Jeżeli x i y to dowolne liczby rzeczywiste to:

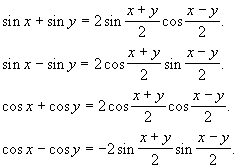
Przykład:

1).Obliczyć: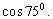

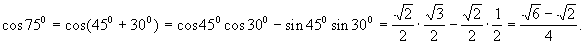
2).Obliczyć: