Zdania w logice to zdania orzekające. Mogą być one fałszywe lub prawdziwe, czyli można określić ich wartość logiczną.
Przykłady:
Łódź to stolica Polski - jest zdaniem fałszywym
Kot to ssak - jest zdaniem prawdziwym
Zdania proste mogą być połączone funktorami zdaniotwórczymi:
 (lub),
(lub),
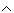 (i),
(i),
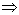 (jeżeli...to...),
(jeżeli...to...),
~ (nieprawda, że...),
dzięki temu utworzymy zdanie złożone.
Zdania proste oznaczamy: p, q, r, s,
a. ~ p oznacza: nieprawda, że p - nazywamy go zaprzeczeniem (negacją zdania).
Negacja zamienia logiczną wartość zdania w przeciwną
Przykład:
zdanie: Dzisiaj jest środa(prawda)
negacja: Nieprawda, że jest dzisiaj środa. (fałsz).
b. p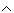 q (p i q) oznacza koniunkcję zdań p oraz q.
q (p i q) oznacza koniunkcję zdań p oraz q.
Koniunkcja jest prawdziwa, wtedy gdy obydwa zdania są prawdziwe. W przeciwnym przypadku jest fałszywa.
Przykład:
zdanie: Warszawa to stolica Polski (prawda). Warszawa jest położona nad Wisłą (prawda), jest zdanie: koniunkcja zdań: Warszawa to stolica Polski i jest ona położona nad Wisłą.
c. p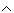 q (p lub q) oznacza alternatywę zdań p i q.
q (p lub q) oznacza alternatywę zdań p i q.
Alternatywa 2 zdań jest prawdą, jeśli co najmniej jedno zdanie jest prawdą, a fałszem, jeśli oba zdania są fałszywe.
Przykład:
zdanie: Zakopane jest położone w górach (prawda). Zakopane jest położone nad morzem (fałsz)
alternatywa zdań: Zakopane jest położone w górach albo nad morzem (prawda).
d. p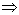 q (jeżeli p to q) oznacza implikację zdań p i q. Zdanie p jest nazywane poprzednikiem implikacji, a zdanie q nazywane jest jej następnikiem.
q (jeżeli p to q) oznacza implikację zdań p i q. Zdanie p jest nazywane poprzednikiem implikacji, a zdanie q nazywane jest jej następnikiem.
Implikacja jest fałszywa wtedy, jeśli poprzednik jest prawdziwy, a następnik fałszywy.
zdanie: Dzisiaj niedziela (fałsz). Nie pójdę do szkoły (prawda),
implikacja zdań: Jeśli dzisiaj niedziela - to nie pójdę do szkoły (prawda).
Kilka praw rachunku zdań
~ ~
~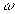
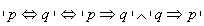
Prawa de Morgana
~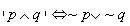
~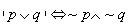

Prawo podwójnego zaprzeczenia.
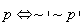
Prawa przemienności

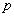
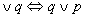
Prawa łączności


Prawa rozdzielności
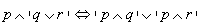
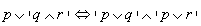
Prawa tautologii
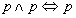
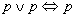
Kwantyfikatory:
"dla każdego x", co oznaczamy symbolem  - jest to tak zwany kwantyfikator ogólny
- jest to tak zwany kwantyfikator ogólny
"istnieje x, takie że" co oznaczamy symbolem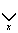 - jest to tak zwany kwantyfikator szczegółowy
- jest to tak zwany kwantyfikator szczegółowy
Przykłady:
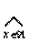 x2
x2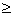 0 (dla każdej liczby rzeczywistej x - kwadrat tej liczby jest nieujemny).
0 (dla każdej liczby rzeczywistej x - kwadrat tej liczby jest nieujemny).
 x2=4 (istnieje taka liczba rzeczywista, której kwadrat równy jest 4)
x2=4 (istnieje taka liczba rzeczywista, której kwadrat równy jest 4)
tak na marginesie: istnieją dwie takie liczby x1= 2, x2= -2
Definicje oraz twierdzenia
Definicje istnieją w matematyce z racji tego, że niektóre pojęcia trzeba zdefiniować.
Pojęcia pierwotne to takie, których nie trzeba definiować, są nimi na przykład: liczba, punkt, zbiór.
Definicja towyrażenie, które opisuje znaczenie danego terminu za pomocą pojęć pierwotnych albo zdefiniowanych wcześniej.
Przykład:
Równoległobok to czworokąt, mający dwie pary równoległych boków.
Jeżeli definicje dotyczą tego samego pojęcia to nazywamy je równoważnymi.
Cała matematyka sformułowana jest w twierdzeniach.
Przybierają one przeważnie postać implikacji: p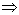 q, czyli wynikania, w którym zdanie p to założenia twierdzenia, natomiast q to teza.
q, czyli wynikania, w którym zdanie p to założenia twierdzenia, natomiast q to teza.
Aksjomaty,czyli pewniki to twierdzenia, które przyjmuje się bez dowodu. Każde inne twierdzenie wymaga dowodu.
Dowód wprost, polega na tym, że wychodzimy z założeń twierdzenia, czyli traktujemy je jako prawdziwe, wyciągamy z nich kolejne wnioski, dochodząc do tego, że teza jest prawdziwa.
Przykład:
Twierdzenie:
Niech a, b, c dowolne liczby rzeczywiste, wtedy:
a > b a + c > b + c
a + c > b + c
Dowód:
a > b a - b > 0
a - b > 0 a + c - b - c > 0
a + c - b - c > 0 a + c - (b + c) > 0
a + c - (b + c) > 0 a + c > b + c.
a + c > b + c.
co należało dowieść (c. n. d.)
Dowód nie wprost - uznajemy założenia twierdzenia jako prawdziwe oraz dołączamy hipotezę, która zaprzecza tezie twierdzenia. Teraz poprzez kolejne wnioski dochodzimy, że hipoteza jest fałszywa z tymi założeniami, albo, że zdanie, które z niej wynika jest fałszywe. Ponieważ uznajemy założenia twierdzenia jako prawdziwe oraz wnioskujemy, że zaprzeczenie tezy jest fałszywe, stąd mamy, że teza twierdzenia jest prawdziwa.
Przykład:
Twierdzenie:
Liczba 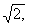 to liczba niewymierna.
to liczba niewymierna.
Dowód:
Zakładamy, że liczba 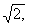 to liczba wymierna, stąd:
to liczba wymierna, stąd: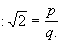
gdzie p i q to liczby całkowite.
Stąd mamy, że, 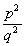 =2, czyli, że p2=2q2,
=2, czyli, że p2=2q2,
zatem p * p=2q *q.
Jeżeli p i q rozłożyć na czynniki pierwsze, 2 musi występować w iloczynie p *p parzystą ilość razy (tyle samo razy w każdym p) lub nie występować wcale, natomiast w iloczynie 2 * q * q nieparzystą ilość razy.
Stąd oba iloczyny nie będą równe.
Z powyższego wynika, że 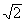 nie jest wymierna wymierną. c. n. d.
nie jest wymierna wymierną. c. n. d.
Zdanie postaci p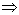 q nazywamy twierdzeniem prostym
q nazywamy twierdzeniem prostym
zdanie q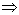 p nazywamy twierdzeniem odwrotnym,
p nazywamy twierdzeniem odwrotnym,
zdanie ~p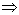 ~q nazywamy twierdzeniem przeciwnym,
~q nazywamy twierdzeniem przeciwnym,
zdanie ~q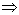 ~p nazywamy twierdzeniem przeciwstawnym albo kontrapozycją twierdzenia.
~p nazywamy twierdzeniem przeciwstawnym albo kontrapozycją twierdzenia.
Twierdzenie proste oraz przeciwstawne są prawdziwe jednocześnie lub jednocześnie fałszywe.
Podobnie jest z twierdzeniem odwrotnym oraz twierdzeniem przeciwstawnym.
Wniosek:
Zamiast dowieść twierdzenie, możemy dowodzić jego kontrapozycję.


