Ruch jest jednym z podstawowych terminów w fizyce. Definicja ruchu: przemieszczenie się elementów układu fizycznego względem układu odniesienia (ruch jest stale względny). Zjawisko ruchu na ogół analizuje się na w odniesieniu do inercjalnego układu odniesienia. Dzieli się je na wiele sposobów.
Głównym rodzajem ruchu jest ruch postępowy – występuje on wówczas kiedy prosta, która łączy 2 możliwe punkty układu. Prosta ta jest równoległa do prostej, która łączy te same punkty w każdym innym momencie występowania ruchu. Również bardzo ważnym rodzajem jest ruch obrotowy.
Gdy weźmiemy pod uwagę cechy kinematyczne ruch można podzielić na prostoliniowy, krzywoliniowy itp. W momencie kiedy będziemy brać pod uwagę cechy dynamiczne, wówczas ruch w inercjalnych układach odniesienia da się dzielić na jednostajny, niejednostajny, jednostajnie przyspieszony i niejednostajnie przyspieszony.
Zajmijmy się na początek ruchem jednostajnym - prędkość wówczas jest stała, przebyta droga równa jest iloczynowi czasu trwania ruchu i prędkości. Za to w ruchu jednostajnie przyspieszonym chwilowa prędkość u jest proporcjonalna do czasu t. Da się to przedstawić w następujący sposób:
v = at,
gdzie
a - przyspieszenie (w ruchu opóźnionym a < 0). Droga s wyraża się wzorem:
s = vot + at2/2,
gdzie
vo - prędkość początkowa.
Ruch niejednostajny:
Opisywany jest on przez spadanie ciał jak oraz przemieszczanie się ciał pod wpływem pola grawitacyjnego (oddziaływanie grawitacyjne). Kiedy będziemy pomijać zmiany natężenia wyżej wymienionego pola wraz z wysokością, wpływem sił oporu aerodynamicznego ruch w pionowym kierunku przy swobodnym spadaniu ciał będziemy mieć do czynienia z ruchem jednostajnie przyspieszonym. Wartość przyspieszenia jest w polu grawitacyjnym taka sama dla wszystkich ciał (Galileusz).
Ruchem jednostajnie przyspieszonym nazywa się ruch, w którym stała jest wartość przyspieszenia. Natomiast dla ruchu krzywoliniowego przyspieszenie rozkłada się na składową styczną do trajektorii (tj. przyspieszenie styczne) i składową do niej prostopadłą (tj. przyspieszenie normalne albo dośrodkowe).
Przyspieszenie (a) - wektorowa wielkość fizyczna (kinematyczna), która opisuje przejścia wektora prędkości ciała (v).
Siła dośrodkowa.
W biegunowych układach współrzędnych przyspieszenie rozkładać można na 2 składowe:
- przyspieszenie radialne
- przyspieszenie transwersalne
Miarą przyspieszenia jest długość podzielona przez kwadrat czasu, jednostką przyspieszenia jest m/s2(w układzie SI).
Przyspieszeniomierz, to urządzenie, przy pomocy którego można zmierzyć przyspieszenie jakiegoś ciała. Wyróżnia się, biorąc pod uwagę typ mierzonego przyspieszenia, przyspieszeniomierze liniowe oraz kątowe. W stosunku do konstrukcji rozróżniamy przyspieszeniomierze: pojemnościowe, indukcyjne, mechaniczne, optyczne, elektromechaniczne, tensometryczne oraz piezoelektryczne.
Prędkość – jest to wektorowa wielkość fizyczna, która wyznacza zmianę położenia ciała w czasie. Chwilową prędkość ciała wyraża się przy pomocy wzoru: V=dr/dt, gdzie: r - wektor położenia ciała. Średnią prędkość można wyliczyć dzieląc przebytą drogę przez czas.
Fizyka klasyczna posługuje się prawem składania prędkości, które jest w rezultacie przekształceniami Galileusza: jeśli 2 ciała przemieszczają się z prędkościami odpowiednio wynoszącymi V1 i V2, to ich względna prędkość wynosi V1 - V2.
Za to w mechanice relatywistycznej względną prędkość wyliczana jest według poniższego wzoru (wynika to z transformacji Lorentza):
 , gdzie
, gdzie 
gdzie: c – jest to prędkość światła w próżni. Jeżeli chodzi o ruchy, które zachodzą w tym samym kierunku powyższy wzór upraszcza się do takiego o to wyrażenia:
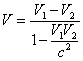
W układzie SI jednostką prędkości jest m/s.
Wektor –to uporządkowana para punktów [A, B], punkt A jest początkiem wektora za to punkt B jest jego końcem. Jeżeli będziemy brać pod uwagę interpretację geometryczną wektor jest to leżący na prostej i zawierający oba punkty A, B ustawiony odcinek ([A, B]= - [B, A]). Kierunek wektora jest to kierunek tej prostej. Zwrotem nazywamy zwrot wyznaczony przez kolejność punktów A oraz B.
Wyróżnia się kilka sposobów notacji wektora.
Składowe wektora – nazywa się nimi różnice odpowiednich współrzędnych jego końca oraz początku Bx - Ax, By - Ay, Bz – Az. Długość wektora jest długością odcinka AB (odległość). Wektorem przeciwnym do danego jest wektor o jednakowej długości oraz kierunku, ale przeciwnym zwrocie. Wektor o jednostkowej długości zwany jest wersorem.
W fizyce występuje również taki o to podział wektorów: swobodne (nie zmieniają się przy translacji) i zaczepione. Dodawanie 2 wektorów zachodzi w taki o to sposób: punkt początkowy drugiego wektora trzeba przesunąć równolegle do końca pierwszego wektora. Suma tych wektorów jest wektorem, który zaczyna się w początku pierwszego wektora natomiast kończy w końcu drugiego wektora. Składowe sumy wektorów są algebraicznymi sumami odpowiednich składowych wektorów pierwotnych. A jeżeli chcemy odjąć 2 wektory to trzeba dodać wektor przeciwny. Mnożenie wektorów przez liczbę jest mnożeniem wszelkich składowych każdej z osobna. Mnożenie 2 wektorów opisywane jest na dwa sposoby, jako iloczyn skalarny lub jako iloczyn wektorowy.


