Podczas ćwiczenia badano zasadę zachowania pędu, wykonując doświadczenie z wahadłem balistycznym skrętnym.
Wahadło balistyczne skrętne, użyte w doświadczeniu, było wypełnione plasteliną. Dzięki temu zderzenie pocisku i wahadła jest całkowicie niesprężyste - następuje utknięcie pocisku w plastelinie. W takim układzie powinna być spełniona zasada zachowania momentu pędu:
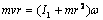
przy czym v jest prędkością początkową pocisku, m jego masą, r odległością miejsca wbicia pocisku od osi obrotu wahadła, I1 to moment bezwładności wahadła a wto prędkość kątowa.
W opisywanym układzie mamy do czynienia ze sprężystym odkształceniem drutu wahadła. Można na tej podstawie zapisać, zgodnie z prawem Hooka, zależność na moment sił sprężystości:
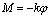
przy czym 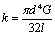 jest sztywnością skrętną drutu, l jego długością, d - średnicą, a G to moduł sprężystości, równy w przypadku stali 8,5 ×104 MPa.
jest sztywnością skrętną drutu, l jego długością, d - średnicą, a G to moduł sprężystości, równy w przypadku stali 8,5 ×104 MPa.
Skręcony w wyniku zderzenia drut ma w takim przypadku maksymalną energię równą 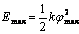 , którą zgodnie z zasadą zachowania energii mechanicznej można zapisać jako
, którą zgodnie z zasadą zachowania energii mechanicznej można zapisać jako
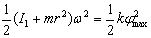
Przez porównanie obydwu równań można wyznaczyć prędkość pocisku:
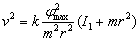
Przy założeniu, że I1 >>mr2 dostajemy równanie
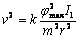
Dodatkowo można założyć, że okres drgań wahadła T >> t, czyli czasu zderzenia.
Aby zbadać, jak porusza się wahadło balistyczne, konieczne jest zapisanie jego równanie ruchu:
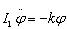
Druga pochodna kąta skręcenia po czasie,  , to przyspieszenie kątowe, natomiast iloczyn kj jest równy momentowi sił sprężystości. Mając tak zapisane równanie ruchu, można je przekształcić do postaci
, to przyspieszenie kątowe, natomiast iloczyn kj jest równy momentowi sił sprężystości. Mając tak zapisane równanie ruchu, można je przekształcić do postaci
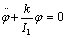
Takie równanie różniczkowe można bardzo prosto rozwiązać metodą przewidywania. Rozwiązaniem ogólnym jest oczywiście funkcja trygonometryczna postaci 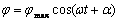 , gdzie jmax to najwyższe skręcenie, a więc amplituda ruchu, natomiast a jest fazą początkową, którą przy odpowiednim doborze warunków pomiaru można przyjąć za równą 0.
, gdzie jmax to najwyższe skręcenie, a więc amplituda ruchu, natomiast a jest fazą początkową, którą przy odpowiednim doborze warunków pomiaru można przyjąć za równą 0.
Z otrzymanych równań można wyznaczyć okres drgań wahadła. Ogólny wzór na okres drgań wygląda następująco: 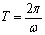
W naszym przypadku częstość drgań, jak wynika z rozwiązania równania różniczkowego, wynosi 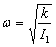 .
.
Przez odpowiednie podstawienie dochodzimy więc do wzoru na okres drgań wahadła:
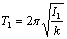
przy określonym momencie bezwładności I1. Jedyną niewiadomą w naszym równaniu jest stała k, czyli sztywność skrętna drutu. Aby wyznaczyć ten współczynnik, należy wykonać pomiary okresu drgań wahadła przy różnych momentach bezwładności, I1 oraz I2, które można zmieniać przesuwając położenie ciężarków na ramionach wahadła. W wyniku pomiarów otrzymamy dwa wyniki:
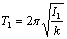 oraz
oraz 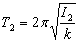 ,
,
z których możemy napisać proporcję
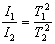
Jeżeli oznaczymy przez DI = I1 - I2, to otrzymamy zależność
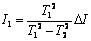
Następnie wynik możemy podstawić do równania na prędkość pocisku:
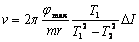
Odpowiednie momenty bezwładności wahadła można bardzo prosto wyznaczyć z równania 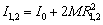 , zmieniając jedynie wartości R, czyli odległości ciężarków od osi obrotu wahadła. Masa ciężarka oraz moment bezwładności samego wahadła były podane w instrukcji do ćwiczenia.
, zmieniając jedynie wartości R, czyli odległości ciężarków od osi obrotu wahadła. Masa ciężarka oraz moment bezwładności samego wahadła były podane w instrukcji do ćwiczenia.
Aby DI = I1 - I2 było większe od zera, należy tak dobrać odległości ciężarków, aby R1 > R2. Otrzymujemy wtedy prostą zależność
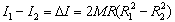
którą możemy podstawić do równania na v:
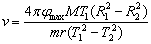
Wszystkie oznaczenia użyte we wzorze pojawiły się już wcześniej, więc nie będę ich powtarzał.
Aby oszacować błąd wyznaczenia prędkości wahadła, należy policzyć różniczkę zupełną z równania
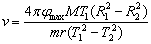
względem parametrów m oraz M, które są obarczone błędem pomiarowym. Otrzymujemy równanie
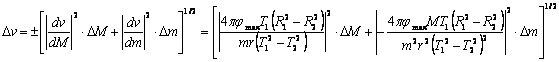
Błąd można policzyć po podstawieniu odpowiednich wartości.
Podczas wyprowadzania końcowego wzoru przyjęto kilka założeń, które mogły mieć wpływ na jakość wyniku końcowego. Pierwszym z założeń było stwierdzenie, że I1 >> mr2. To uproszczenie nie ma wpływu na dokładność wyznaczania prędkości wahadła, ponieważ moment bezwładności pocisku jest rzeczywiście bardzo niewielki w porównaniu z momentem bezwładności wahadła balistycznego. Gdyby takie założenie zostało zastosowane a w rzeczywistości moment bezwładności pocisku byłby porównywalny z momentem bezwładności wahadła, to nasz wynik byłby bardzo niedokładny - rzeczywista prędkość pocisku byłaby znacznie większa od otrzymanej z powyższych obliczeń.
Kolejne uproszczenie było oparte o założenie, że okres drgań wahadła jest znacznie dłuższy niż czas oddziaływania wahadła i pocisku, czyli że T >> t. Takie założenie ma swoje uzasadnienie w tym, że czas zderzenia pocisku i wahadła, dany równaniem 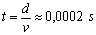 , jest znikomo mały w porównaniu do okresu drgań wahadła balistycznego. Takie założenie w bardzo dużym stopniu upraszcza nasze równanie, nie powodując żadnego negatywnego wpływu na wyniki. W przypadku, gdy okres drgań wahadła jest porównywalny z czasem oddziaływania, przyjmuje się założenie, że siła działająca na wahadło nie jest stała, ale zmienia się w czasie. To powoduje bardzo poważną komplikację równań.
, jest znikomo mały w porównaniu do okresu drgań wahadła balistycznego. Takie założenie w bardzo dużym stopniu upraszcza nasze równanie, nie powodując żadnego negatywnego wpływu na wyniki. W przypadku, gdy okres drgań wahadła jest porównywalny z czasem oddziaływania, przyjmuje się założenie, że siła działająca na wahadło nie jest stała, ale zmienia się w czasie. To powoduje bardzo poważną komplikację równań.


