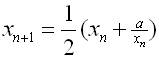Jak komputer oblicza pierwiastek kwadratowy z dowolnej liczby?
Aby obliczyć pierwiastek kwadratowy z liczby a, można postępować w następujący sposób (jest to tzw. algorytm Newtona-Raphsona):
Weź dowolną liczbę x1. Każdą następną liczbę wylicz ze wzoru:
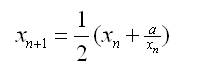
Postępowanie to kontynuujemy, dopóki któraś z kolejnych obliczonych liczb będzie wystarczająco dokładnym przybliżeniem pierwiastka z a. Jeśli chcemy, by dokładność wynosiła d, to wyliczamy kolejne liczby xn, dopóki nie zajdzie warunek |xn-xn-1| Przykład. Policzymy pierwiastek kwadratowy z liczby 2. weźmy x1=3. Obliczamy kolejne liczby według podanego wzoru: x2=(1/2)(3+(2/3))=11/6 x3=(1/2)(11/6+(2/(11/6)))=193/132=1,46(21) x4=(1/2)(193/132+(2/(193/132)))=72097/50952=1,41499.... Im dłużej będziemy wyliczać kolejne liczby, tym dokładniejsze otrzymamy przybliżenie. Dlaczego ta metoda działa? Dlatego, że granicą ciągu (gdzie x1 jest dowolną liczbą) jest właśnie pierwiastek z liczby a. Jeśli za pierwszą liczbę przyjmiemy liczbę, która różni się bardzo od pierwiastka z a, będziemy musieli wykonać wiele obliczeń, żeby osiągnąć żądaną dokładność. Dlatego jako pierwszą liczbę x1 dobrze jest przyjąć mniej więcej przybliżenie pierwiastka z a. Na przykład, jeśli chcemy obliczyć pierwiastek z 10, to o wiele sensowniej jako x1 przyjąć liczbę 3 niż np. liczbę 1000 (bo 3 jest mniej więcej przybliżeniem pierwiastka z 10).