Stosując metodę przeciwnych współczynników doprowadzamy układ równań do takiej postaci, aby:
1) jeżeli przy x jest współczynnik a w pierwszym równaniu, to drugi równanie przekształcamy tak, aby przy x był współczynnik - a albo szukamy wspólnych przeciwnych współczynników
lub
2) jeżeli przy y jest współczynnik b w pierwszym równaniu, to drugi równanie przekształcamy tak, aby przy y był współczynnik - b albo szukamy wspólnych przeciwnych współczynników
W ten sposób możemy dodać równania stronami, przez co wyeliminujemy jedną zmienną.
Z tak powstałego równania możemy obliczyć pozostałą zmienną, a za jej pomocą drugą, wstawiając ją do dowolnego równania z podstawowego układu równań.
Przykład:
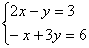
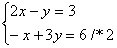
+
dodajemy równania stronami i otrzymujemy:
2x - y -2x +6y = 3 + 12
5y = 15
y = 3
Wstawiamy tą wartość do pierwszego równania z podstawowego układu równań:
2x - y = 3
2x - 3 = 3
przenosimy -3 na drugą stronę równania:
2x = 3 + 3
2x = 6 /:2
x = 3
Sprawdzenie:
Wstawiamy otrzymane wartości do wyjściowego układu równań:
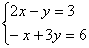 =>
=> 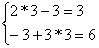 =>
=> 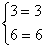
Czyli mamy pewność co do prawidłowości naszych obliczeń.


