f: U®U - endomorfizm U(K)
Definicja 1: Wektor własny endomorfizmu
Wektor vÎU (niezerowy) jest wektorem własnym endomorfizmu f jeżeli $lÎK
takia, że (1) f(v) = lv .
l nazywamy wartością własną endomorfizmu f
B =(e1,...,en) - baza U A = Mf(B)
Y=AX
f(v)-lv = 0 f(v) - lId(v) = 0 (2) (f - lId)(v) = 0 (3) (A - lE)X = 0 - postać macierzowa (2)
W celu znalezienia wektora własnego v endomorfizmu, należy znaleźć rozwiązanie niezerowe układu (3). Aby ono istniało musi zachodzić: det(A-lE) = 0
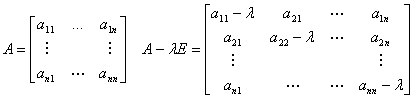
det(A-lE) = (-1)n (ln + an-1 ln-1+ ... + a1l + a0)
Wartości własne endomorfizmu f to pierwiastki równania:
ln + an-1 ln-1+ ... + a1l + a0= 0
j(l) = ln + an-1 ln-1+ ... + a1l + a0-wielomian charakterystyczny
Twierdzenie 1
Wielomian charakterystyczny endomorfizmu f nie zależy od wyboru bazy.
Dowód Tw. 1
A = Mf(B) A' = Mf(B')
j(l) = det(A - lE) y(l) = det(A' - lE)
y(l) = det(A' - lE) = det(P-1AP - lP-1EP) = det P-1(A - lE) P = det P-1 det(A - lE) det P =
= (det P)-1 det(A - lE) det P = det(A - lE) = j(l)
cnu
Wartości własne i ich krotności endomorfizmu f nie zależą od wyboru bazy.
Wektory własne endomorfizmu f nie zależą od wyboru bazy.
Definicja 2 Wektory własne macierzy
Niech A macierz kwadratowa
niech aij ÎK
Wektory własne macierzyA to wektory własne endomorfizmu f : Kn ® Kn
Wartości własne macierzyA to pierwiastki równania det(A - lE) = 0
Wektory własne macierzy A to rozwiązania układu (E - lE) X = 0
Twierdzenie 2
Założenia:
l jest wartością własną endomorfizmu f, Ul = {vÎU : (f - lId)(v) = 0} = Ker(f - lId)
Teza:
Ul - podprzestrzeń wektorowa przestrzeni U.
Ul zawiera wszystkie wektory własne endomorfizmu f, które odpowiadają wartości własnej l oraz zawiera dodatkowo wektor 0.
Definicja 3
Podprzestrzeń Ul nazywamy podprzestrzenią własna endomorfizmu f.
Definicja 4
A - macierz kwadratowa, aijÎK, l - wartość własna macierzy A
Podprzestrzenią własną macierzy nazywa się zbiór rozwiązań układu (A - lE) X = 0.
Twierdzenie 3
Założenia:
A = [aij]n x n j(l) = (l- l1)k1... (l - ls)ks
l1,...,ls - wartości własne (różne)
k1+...+ks = n
Teza:
Uli - podprzestrzeń własna, która odpowiada wartości własnej li
1 <= dim Uli <= ki ki - krotności wartości własnej wielomianu charakterystycznego
Twierdzenie 4
Wektory własne, które odpowiadają różnym wartościom własnym są liniowo niezależne.
Dowód Tw. 4
Założenia:
v1, ..., vs wektory własne, które odpowiadają wartościom własnym l1, ..., ls (l1, ..., ls różne między sobą)
1° s = 1 v1 ( v1 ¹ 0 to układ (v1) liniowo niezależny )
2° zakładamy, że v1, ..., vk liniowo niezależne
Teza: v1, ..., vk, vk+1 liniowo niezależne
Dowód :
(1. a1v1 + ... + akvk + ak+1vk+1 = 0
Przypuśćmy, że v1, ..., vk, vk+1 liniowo zależne Þ $ai ( i= 1,..., k+1) ai ¹ 0
(2. a1f(v1) + ... + ak+1f(vk+1) = 0
(3. a1l1v1 + ... + ak+1lk+1vk+1 = 0
(1)/lk+1 : (4) a1lk+1 + ... + ak+1lk+1vk+1 = 0
(3) - (4) : a1(l1-lk+1)v1 + ... + ak(lk-lk+1)vk = 0
wśród a1, ..., ak musi  niezerowy współczynnik
niezerowy współczynnik
niech ai ¹ 0 oraz stąd, że v1, .. ,vk liniowo niezależne Þa1(l1-lk+1) = 0, ..., ak(lk-lk+1) = 0
ai¹0 Þli - lk+1 = 0 Þ li = lk+1 dostajemy sprzeczność z założeniem o równości wartości własnych.
co kończy dowód 
A = [aij]n x n j(l) = (l- l1)k1... (l - ls)ks
l1,...,ls - wartości własne (różne)
założenia:
dim Uli = ki " i = 1,2,...,s
v11,...,v1ks - wektory liniowo niezależne, baza Ul1
v21,...,v2ks- wektory liniowo niezależne, baza Ul2
...
vs1,...,vsks - wektory liniowo niezależne, baza Uls
Twierdzenie 5
v11,...,v1k1,v21,...,v2k2,...,vs1,...,vsks liniowo niezależne
wektory te możemy przyjąć jako bazę przestrzeni U.
f: U®U endomorfizm A = Mf(B)
B' - baza składające się z wektorów własnych
B' = (v11,...,v1k1,v21,...,v2k2,...,vs1,...,vsks)
Mf(B') = ?
f(v11) = l1v11 = [l1, 0, 0, ...,0]B'
f(v12) = l1v12 =, [0, l1, 0, ...,0]B'
...
f(v1k1) = l1v1k1 = [0,..., l1, 0, ...,0]B' - l1 na pozycji k1
f(v21) = l1v21 = [0,..., l21, 0, ...,0]B' - l2 na pozycji k1+1
...
f(vs1) = l1vs1 = [0,..., ls, 0, ...,0]B'
...
f(vsks) = l1v11 = [0,..., 0, ls]B'
 D =P-1AP
D =P-1AP
P - macierz przejścia z bazy B do bazy B' składająca się z wektorów własnych.
Twierdzenie 6
Jeśli B jest bazą złożoną z wektorów własnych, to Mf(B) jest diagonalna.
Twierdzenie odwrotne:
Gdy macierz endomorfizmu f w B = (e1, ..., en) jest diagonalna to składa się ona z wektorów własnych
Dowód Tw. 6
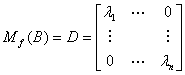
z definicji macierzy odwzorowania liniowego mamy:
f(e1) = [l1, 0, ..., 0]B Þ f(e1) =l1e1
...
f(en) = [ln, 0, ..., 0]B Þ f(en) =lnen
Þ stąd e1, ..., en to wektory własne odpowiednich wartości l1, ..., ln
Definicja 5
Endomorfizm f jest diagonalizowalny gdy istnieje taka baza, że macierz endomorfizmu w tej bazie jest diagonalizowalna.
Endomorfizm jest diagonalizowalny, gdy istnieje dla niego baza, która składa się z wektorów własnych, co zachodzi wtedy, gdy dim Uli = ki .
Wniosek
Gdy wartości własne są jednokrotne, wtedy endomorfizm jest diagonalizowalny.
Gdy wartości własne są wielokrotne to dim Uli= ki
A = Mf(B) D = Mf(B') gdzie B' jest macierzą złożoną z wektorów własnych endomorfizmu f.
D = P-1AP gdzie P jest macierzą przejścia z bazy B do bazy B'.
Macierz A jest podobna do D. Oznaczenie: A ~ D
Definicja 6
A Î Mn x n A uważamy za macierz odwzorowania f : Rn®Rn w bazie kanonicznej.
Wartości własne, wektory własne oraz podprzestrzenie własne macierzy A są warunkami wystarczającymi endomorfizmu f
Definicja 7
Macierz jest diagonalizowalna, gdy istnieje macierz nieosobliwa P oraz macierz diagonalizowalna D taka, że D=P-1AP