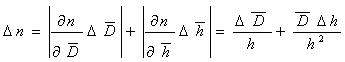Opracowanie wyników
Wyniki otrzymane dla płytki szklanej:
|
D [mm]
|
d1 [mm]
|
d2 [mm]
|
D [mm]
|
d1 [mm]
|
d2 [mm]
|
h=(d2 - d1)
|
n
|
|
gr. rzeczywista
|
górna pow.
|
dolna pow.
|
śr. arytm.
|
śr. arytm
|
śr. arytm.
|
gr. pozorna
|
wsp. załam.
|
|
1,14
|
6,55
|
7,25
|
1,15
|
6,553
|
7,256
|
0,703
|
1,636
|
|
1,14
|
6,54
|
7,27
| | | | | |
|
1,16
|
6,57
|
7,26
| | | | | |
|
1,14
|
6,53
|
7,28
| | | | | |
|
1,15
|
6,58
|
7,24
| | | | | |
|
1,17
|
6,57
|
7,26
| | | | | |
|
1,15
|
6,54
|
7,25
| | | | | |
|
1,15
|
6,56
|
7,27
| | | | | |
|
1,15
|
6,56
|
7,25
| | | | | |
|
1,15
|
6,53
|
7,23
| | | | | |
|
11,5
|
65,53
|
72,56
| | | | |
suma
|
Wyniki otrzymane dla płytki z plexiglasu:
|
D [mm]
|
d1 [mm]
|
d2 [mm]
|
D [mm]
|
d1 [mm]
|
d2 [mm]
|
h=(d2 - d1)
|
n
|
|
gr. rzeczywista
|
górna pow.
|
dolna pow.
|
śr. arytm.
|
śr. arytm
|
śr. arytm.
|
gr. pozorna
|
wsp. załam.
|
|
2,76
|
4,91
|
6,5
|
2,759
|
4,947
|
6,544
|
1,597
|
1,728
|
|
2,77
|
4,93
|
6,58
| | | | | |
|
2,76
|
4,95
|
6,55
| | | | | |
|
2,76
|
4,95
|
6,5
| | | | | |
|
2,74
|
4,97
|
6,59
| | | | | |
|
2,74
|
4,99
|
6,55
| | | | | |
|
2,76
|
4,94
|
6,57
| | | | | |
|
2,76
|
4,92
|
6,51
| | | | | |
|
2,76
|
4,98
|
6,53
| | | | | |
|
2,78
|
4,93
|
6,56
| | | | | |
|
27,59
|
49,47
|
65,44
| | | | |
suma
|
Obliczenia pomocnicze:
Płytka ze szkła:
|
( d1 - d1 )
|
( d2 - d2 )
|
(d2-d1 - (d1-d2))
|
|
9E-06
|
3,6E-05
|
9E-06
|
|
0,000169
|
0,000196
|
0,000729
|
|
0,000289
|
1,6E-05
|
0,000169
|
|
0,000529
|
0,000576
|
0,002209
|
|
0,000729
|
0,000256
|
0,001849
|
|
0,000289
|
1,6E-05
|
0,000169
|
|
0,000169
|
3,6E-05
|
4,9E-05
|
|
4,9E-05
|
0,000196
|
4,9E-05
|
|
4,9E-05
|
3,6E-05
|
0,000169
|
|
0,000529
|
0,000676
|
9E-06
|
|
0,00281
|
0,00204
|
0,00541
|
Płytka z plexiglasu:
|
( d1 - d1 )
|
( d2 - d2 )
|
(d2-d1 - (d1-d2))
|
|
0,001369
|
0,001936
|
4,9E-05
|
|
0,000289
|
0,001296
|
0,002809
|
|
9E-06
|
3,6E-05
|
9E-06
|
|
9E-06
|
0,001936
|
0,002209
|
|
0,000529
|
0,002116
|
0,000529
|
|
0,001849
|
3,6E-05
|
0,001369
|
|
4,9E-05
|
0,000676
|
0,001089
|
|
0,000729
|
0,001156
|
4,9E-05
|
|
0,001089
|
0,000196
|
0,002209
|
|
0,000289
|
0,000256
|
0,001089
|
|
0,00621
|
0,00964
|
0,01141
|
Kolejne etapy obliczeń:
- Średnią grubość płytki policzyłem ze wzoru:
![00029730.gif]() .
. - Wartość średnią wskazań czujnika przy ustawieniach mikroskopu na ostrość górnej i dolnej powierzchni płytki obliczyłem ze wzorów:
![00029731.gif]() ,
, ![00029732.gif]() .
. - Średnia grubość pozorna
![00029733.gif]() .
. - Współczynnik załamania światła obliczyłem ze wzoru:
![00029734.gif]() .
. - Błąd wyznaczenia wartości średniej wskazań czujnika oraz błąd grubości pozornej wyznaczam korzystając z zależności na błąd średni kwadratowy, czyli odpowiednio:
![00029735.gif]() ,
, ![00029736.gif]() ,
, ![00029737.gif]() , gdzie n = 10 liczba pomiarów. Błąd pomiaru grubości rzeczywistej jest równy dokładności śruby mikrometrycznej
, gdzie n = 10 liczba pomiarów. Błąd pomiaru grubości rzeczywistej jest równy dokładności śruby mikrometrycznej ![00029738.gif]() = 0,01 mm.
= 0,01 mm.
Otrzymane wyniki:
Dla płytki ze szkła:
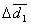 = 0,006 mm
= 0,006 mm
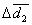 = 0,005 mm
= 0,005 mm
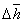 = 0,008 mm
= 0,008 mm
Dla płytki z plexiglasu:
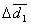 = 0,008 mm
= 0,008 mm
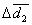 = 0,01 mm
= 0,01 mm
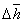 = 0,011 mm
= 0,011 mm
- Obliczam błąd względny wyników otrzymanych powyżej:
Dla płytki ze szkła:
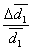 = 0,09 %
= 0,09 %
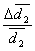 = 0,07 %
= 0,07 %
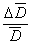 = 0,9 %
= 0,9 %
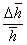 = 1,14 %
= 1,14 %
Dla płytki z plexiglasu:
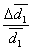 = 0,16 %
= 0,16 %
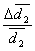 = 0,15 %
= 0,15 %
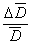 = 0,4 %
= 0,4 %
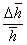 = 0,69 %
= 0,69 %
- Ponieważ wyznaczając współczynnik załamania dokonujemy dwóch pomiarów grubości płytki (rzeczywistej D i pozornej h) i oba oznaczone są błędem, wiec błąd względny pomiaru tego współczynnika można wyznaczyć korzystając z prawa przenoszenia błędów. Niepewność wyznaczenia współczynnika załamania światła n obliczam stosując metodę różniczki zupełnej. Wyprowadzenie wzoru z którego będę korzystał jest następujące:
![00029753.gif]()
Płytka ze szkła:
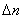 = 0,032
= 0,032
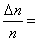 2 %
2 %
Płytka z plexiglasu:
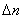 = 0,018
= 0,018
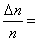 1 %
1 %
- Ostateczny rezultat pomiaru:
Płytka ze szkła: n = 1,636 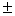 0,032
0,032
Płytka z plexiglasu: n = 1,728 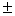 0,018
0,018
Wnioski
Celem tego ćwiczenia było wyznaczenie współczynnika załamania światła dla ciał stałych metodą mikroskopu.. Aby obliczyć współczynnik załamania światła płytki musiałem zmierzyć grubość rzeczywistą płytki śrubą mikrometryczną. Zauważyłem jednak że kiedy dokręciłem śrubę mikrometryczną do końca, grubość wskazywana przez wskaźnik wynosiła -0,02 mm zamiast 0. Spowodowałoby to powstanie błędu systematycznego, dlatego do pomiarów śrubą mikrometryczną automatycznie dodałem 0,02 mm. Grubość pozorną wyznaczyłem przy pomocy mikroskopu mierząc przesunięcie tubusa mikroskopu między położeniami ostrego widzenia kresek umieszczonych na obu powierzchniach płytki.
Zastosowana w ćwiczeniu metoda wyznaczania współczynnika załamania światła okazała się dosyć skuteczna, ponieważ otrzymane wartości okazały się być zbliżone do tablicowych wartości. Załamanie światła dla szkła wynosi, w zależności od rodzaju, od 1,4 do 1,9. Otrzymane wyniki mieszczą się zatem w tych granicach. Mając na uwadze niewielkie błędy, spowodowane głownie niedokładnością urządzenia pomiarowego oraz oka ludzkiego, stwierdzam że doświadczenie zostało przeprowadzone prawidłowo i zakończyło się satysfakcjonującym rezultatem.
Przy badaniu zależności współczynnika załamania od długości fali padającego światła powinniśmy stwierdzić, że wraz z wzrostem długości fali maleje wartość tego współczynnika. Należy jednak zwrócić uwagę na to, że błędy współczynnika załamania światła które otrzymałem, są zbyt duże w porównaniu do różnicy między kolejnymi wartościami współczynnika dla różnych długości fal, aby można było jednoznacznie stwierdzić, jaki jest wpływ długości fali na współczynnik załamania. Wnioskuję więc że powyższa metoda nie nadaje się do wyznaczenia zależności współczynnika załamania światła od długości fali.

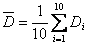 .
.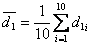 ,
, 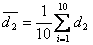 .
.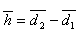 .
.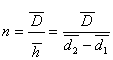 .
.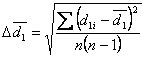 ,
, 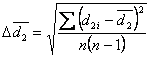 ,
, 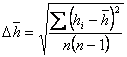 , gdzie n = 10 liczba pomiarów. Błąd pomiaru grubości rzeczywistej jest równy dokładności śruby mikrometrycznej
, gdzie n = 10 liczba pomiarów. Błąd pomiaru grubości rzeczywistej jest równy dokładności śruby mikrometrycznej 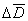 = 0,01 mm.
= 0,01 mm.