- Otrzymane Wyniki:
Energię fotonu otrzymałem ze wzoru: 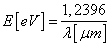
|
Długość Fali [nm]
|
Współczynnik Transmisji [%]
|
Energia Fotonu [eV]
|
|
390
|
1
|
3,178462
|
|
395
|
2
|
3,138228
|
|
400
|
4
|
3,099
|
|
405
|
5
|
3,060741
|
|
410
|
7
|
3,023415
|
|
415
|
10
|
2,986988
|
|
420
|
15
|
2,951429
|
|
425
|
19
|
2,916706
|
|
430
|
24
|
2,882791
|
|
435
|
30
|
2,849655
|
|
440
|
35
|
2,817273
|
|
445
|
39
|
2,785618
|
|
450
|
44
|
2,754667
|
|
455
|
49
|
2,724396
|
|
460
|
52
|
2,694783
|
|
465
|
56
|
2,665806
|
|
470
|
58
|
2,637447
|
|
475
|
61
|
2,609684
|
|
480
|
64
|
2,5825
|
|
485
|
67
|
2,555876
|
|
490
|
69
|
2,529796
|
|
495
|
69
|
2,504242
|
|
500
|
69
|
2,4792
|
|
505
|
70
|
2,454653
|
|
510
|
71
|
2,430588
|
|
515
|
72
|
2,40699
|
|
520
|
74
|
2,383846
|
|
525
|
75
|
2,361143
|
|
530
|
75
|
2,338868
|
|
535
|
75
|
2,317009
|
|
540
|
74
|
2,295556
|
|
545
|
74
|
2,274495
|
|
550
|
76
|
2,253818
|
|
555
|
77
|
2,233514
|
|
560
|
78
|
2,213571
|
|
565
|
78
|
2,193982
|
|
570
|
77
|
2,174737
|
|
Długość Fali [nm]
|
Współczynnik Transmisji [%]
|
Energia Fotonu [eV]
|
|
575
|
76
|
2,155826
|
|
580
|
74
|
2,137241
|
|
585
|
73
|
2,118974
|
|
590
|
73
|
2,101017
|
|
595
|
74
|
2,083361
|
|
600
|
75
|
2,066
|
|
605
|
76
|
2,048926
|
|
610
|
78
|
2,032131
|
|
615
|
79
|
2,01561
|
|
620
|
78
|
1,999355
|
|
625
|
77
|
1,98336
|
|
630
|
76
|
1,967619
|
|
635
|
74
|
1,952126
|
|
640
|
73
|
1,936875
|
|
645
|
74
|
1,92186
|
|
650
|
75
|
1,907077
|
|
655
|
76
|
1,892519
|
|
660
|
78
|
1,878182
|
|
665
|
79
|
1,86406
|
|
670
|
80
|
1,850149
|
|
675
|
81
|
1,836444
|
|
680
|
82
|
1,822941
|
|
685
|
81
|
1,809635
|
|
690
|
80
|
1,796522
|
|
695
|
79
|
1,783597
|
|
700
|
79
|
1,770857
|
|
705
|
77
|
1,758298
|
|
710
|
76
|
1,745915
|
|
715
|
75
|
1,733706
|
|
720
|
74
|
1,721667
|
|
725
|
75
|
1,709793
|
|
730
|
76
|
1,698082
|
|
735
|
76
|
1,686531
|
|
740
|
77
|
1,675135
|
|
745
|
76
|
1,663893
|
|
750
|
76
|
1,6528
|
|
755
|
76
|
1,641854
|
- Analizując eksperymentalną zależność współczynnika transmisji od długości fali, stwierdzam, że można wyróżnić dwa obszary:
- w pierwszym obszarze transmisja jest niska, co oznacza, że poziom absorpcji jest wysoki
- w drugim obszarze przy wysokiej transmisji absorpcja jest niska
W obszarze słabej absorpcji, gdy grubość cienkiej warstwy wykresie jest porównywalna wykresie długością fali λ, wykresie wyniku interferencji pojawiają się charakterystyczne oscylacje współczynnika transmisji T. Z wykresu odczytuję wartości, Tmax i Tmin współczynnika transmisji w obszarze słabej absorpcji: Tmax = 82 % i Tmin = 73 %.
Obliczam współczynnik załamania warstwy n korzystając z następujących wzorów: 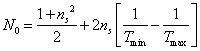
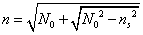 ,
,
gdzie ns jest współczynnikiem załamania podłoża (dla szkła ns = 1,52).
Po podstawieniu wartości liczbowych otrzymuję:
N0 = 2,11; n = 1,89.
- Wyliczam grubość d cienkiej warstwy półprzewodnika według wzoru:
![00029641.gif]()
- Wyznaczam długości fal λ1 i λ2 odpowiadające dwóm kolejnym maksimom lub minimom interferencyjnym współczynnika transmisji T. Wyznaczam je dla maksimów: λ1=615 nm λ2=680 nm. Korzystając z uzyskanych danych obliczam d = 2,116 μm.
- Obliczam współczynnik załamania światła na granicy powietrze-warstwa R12 oraz warstwa-szkło R23 :
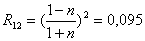
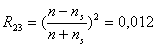
Obliczam zależność współczynnika absorpcji α w zależności od energii fotonu E.
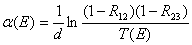
Wzór ten jest prawdziwy w obszarze silnej absorpcji.(czyli dla E>2,6 eV).
Wyznaczam współczynnik absorpcji:
|
Energia [eV]
|
Współczynnik absorpcji
|
|
3,178462
|
2123081,958
|
|
3,138228
|
1795569,086
|
|
3,099
|
1468056,215
|
|
3,060741
|
1362620,62
|
|
3,023415
|
1203637,086
|
|
2,986988
|
1035107,748
|
|
2,951429
|
843525
|
|
2,916706
|
731831,0198
|
|
2,882791
|
621447,7233
|
|
2,849655
|
516012,1285
|
|
Energia [eV]
|
Współczynnik absorpcji
|
|
2,817273
|
443175,748
|
|
2,785618
|
392044,6998
|
|
2,754667
|
335047,8314
|
|
2,724396
|
284192,2139
|
|
2,694783
|
256114,5767
|
|
2,665806
|
221098,4712
|
|
2,637447
|
204517,7806
|
|
2,609684
|
180689,142
|
|
2,5825
|
158004,7285
|
|
2,555876
|
136359,668
|
- Aby wyznaczyć przerwę energetyczną Eg najwygodniej jest wykreślić zależność
![00029645.gif]() dla:
dla:
- m = 0,5 - przejścia proste dozwolone
- m = 1,5 - przejścia proste wzbronione
- m = 2 - przejścia skośne dozwolone
- m = 3 - przejścia skośne wzbronione
-
|
Energia fotonu [eV]
|
f(E)
| |||
|
m=1/2
|
m=3/2
|
m=2
|
m=3
| |
|
3,178462
|
4,55373E+13
|
35709,94216
|
2597,717
|
188,9707
|
|
3,138228
|
3,17522E+13
|
31665,8435
|
2373,795
|
177,949
|
|
3,099
|
2,0698E+13
|
27456,35247
|
2132,957
|
165,6996
|
|
3,060741
|
1,73941E+13
|
25910,01517
|
2042,212
|
160,9659
|
|
3,023415
|
1,3243E+13
|
23658,9526
|
1907,641
|
153,8147
|
|
2,986988
|
9,55956E+12
|
21223,28895
|
1758,367
|
145,6822
|
|
2,951429
|
6,19813E+12
|
18369,05539
|
1577,848
|
135,5325
|
|
2,916706
|
4,55624E+12
|
16578,13356
|
1461,005
|
128,7561
|
|
2,882791
|
3,20949E+12
|
14750,6721
|
1338,471
|
121,4523
|
|
2,849655
|
2,16224E+12
|
12931,08044
|
1212,624
|
113,7149
|
|
2,817273
|
1,55887E+12
|
11594,97772
|
1117,384
|
107,68
|
|
2,785618
|
1,19265E+12
|
10604,85567
|
1045,03
|
102,9799
|
|
2,754667
|
8,51828E+11
|
9479,466804
|
960,7003
|
97,36255
|
|
2,724396
|
5,99466E+11
|
8431,824607
|
879,9159
|
91,82497
|
|
2,694783
|
4,76339E+11
|
7809,777994
|
830,7666
|
88,37295
|
|
2,665806
|
3,47399E+11
|
7029,798924
|
767,7276
|
83,8439
|
|
2,637447
|
2,90958E+11
|
6626,382793
|
734,4418
|
81,4026
|
|
2,609684
|
2,22351E+11
|
6058,242813
|
686,6889
|
77,83471
|
|
2,5825
|
1,66503E+11
|
5501,404895
|
638,7857
|
74,17146
|
|
2,555876
|
1,21465E+11
|
4952,416662
|
590,3545
|
70,37341
|
- Dopasowuję prostą wzorcowej zależności metodą najmniejszych kwadratów, korzystając z programu Origin, do punktów eksperymentalnych. Otrzymuję wyniki:
Eg1 » 2,7 eV dla m= 0,5
Eg2 » 2,53 eV dla m=1,5
Eg3 » 2,43 eV dla m=2
Eg4 » 2,23 eV dla m=3
Tylko dla przejść prostych dozwolonych wartość przerwy energetycznej leży w obszarze silnej absorpcji. Zatem wartość przerwy energetycznej wynosi Eg = 2,7 eV.
- Błędy w wynikach wynikają przede wszystkim ze sposobu przeprowadzania doświadczenia. Konieczność dokonywania dużej liczby pomiarów i każdorazowej kalibracji przyrządu przed kolejnym pomiarem, mogła spowodować niedokładne odczytanie wartości. Również analogowy charakter przyrządów pomiarowych (drgająca wskazówka) uniemożliwił dokładniejszy pomiar. Dochodzi jeszcze błąd paralaksy i zbyt drobnego wyskalowania tarczy ze wskazówką. Podsumowując wynik przeprowadzonego ćwiczenia uznaje za satysfakcjonujący, aczkolwiek do przeprowadzania tego typu doświadczenia znacznie dokładniejsze odczyty dokonywałoby się z aparatury cyfrowej.

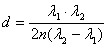
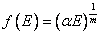 dla:
dla:
