Badanie pojemności złącza PN

Cel ćwiczenia.

Celem ćwiczenia jest zbadanie pojemności złącza P­-N różnorodnych diod i złącz tranzystorowych w zakresie bezpiecznych napięć rewersyjnych.

Opracowanie wyników.

W złączu p-n można zaobserwować zjawiska które świadczą o tym, że posiada ono pewną pojemność. Wyróżnić tu można pojemność warstwy złączową C_j i pojemność dyfuzyjną C_d, które związane są właściwościami złącz p-n, oraz pewną pojemność C_p, zwaną pojemnością pasożytniczą, związaną z technologią wytwarzania złącza. Pojemności C_j i C_d są silnie nieliniowo zależne od napięcia polaryzującego U i wyrażają się wzorami:

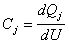 gdzie: Q_j - ładunek złączowy

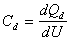 gdzie: Q_d - ładunek dyfuzyjny

Złącze p-n można zatem traktować jako nieliniową pojemność C = C_j + C_d + C_p

Można dowieść, że 

 

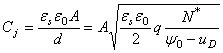
gdzie: y₀ - potencjał kontaktowy złącza

• - przenikalność dielektryczna półprzewodnika i próżni

N* = N_AN_D/(N_A+N_D), - koncentracja efektywna

W przypadku ogólnym pojemność złączową przestawiamy w zależności empirycznej

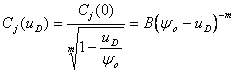 gdzie B=C_j(0)y_o^-m.

Obwód rezonansowy użyty w wykonywanym ćwiczeniu został dołączony do wzmacniacza operacyjnego o dużym wzmocnieniu, składa się ze stałej indukcyjności L i pojemności pasożytniczej C_p, wynikającej głównie z montażu, oraz z dołączanej pojemności diody C (lub wzorcowej C_w). Częstotliwość drgań takiego obwodu, zgodnie ze wzorem Thomsona, wynosi

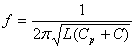co po przekształceniu daje wzór na pojemność zewnętrzną

Aby określić wszystkie parametry obwodu rezonansowego wykonaliśmy trzy pomiary. Przy pojemnościach wzorcowych częstotliwości drgań wynoszą zatem

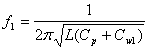 oraz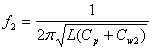  

Po podzieleniu stronami powyższych zależności uzyskamy wyrażenie na C_p

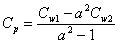 gdzie a=f₁/f₂.

Indukcyjność L obliczam korzystając z jednego z uzyskanych pomiarów:

 

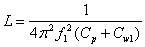
Uzyskane wyniki dla par: C₁C₂, C₁C₃, C₂C₃:

fw1 [MHz]	fw2[MHz]	Cw1[pF]	Cw2[pF]	a= f1/f2	Cp[pF]	L[μH]
3,62	3,08	27,05	68,35	1,17	82,54	17,68
3,08	2,92	68,35	84,75	1,05	78,46	18,17
3,62	2,92	27,05	84,75	1,24	81,68	17,82

C_p średnie 80,89 pF 

Błąd C_p wynosi 0,51 pF 

L średnie 17,89 µH 

Błąd L wynosi 0,06 µH 

Na podstawie otrzymanych wartości C_p i L obliczam wartości pojemności złączowej trzech różnych diod dla kolejnych częstotliwości rezonansowych wg wzoru:

 

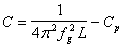
Dioda nr 1
U[V]	F[MHz]	C[pF]
-0,02	3,19	58,65
-0,42	3,54	32,53
-0,79	3,65	25,26
-1,06	3,69	23,03
-1,35	3,72	21,31
-1,74	3,75	19,74
-2,15	3,78	18,46
-2,61	3,80	17,37
-3,24	3,82	16,24
-4,11	3,84	15,03
-4,66	3,86	14,43
-5,46	3,87	13,79
-5,95	3,88	13,40
-6,45	3,88	13,06

Dioda nr 2
U[V]	F[MHz]	C[pF]
-0,19	2,83	96,42
-0,25	2,89	88,92
-0,37	3,00	76,49
-0,51	3,10	66,50
-0,73	3,22	55,81
-1,02	3,31	48,55
-1,31	3,36	44,50
-1,57	3,40	41,79
-2,09	3,46	37,78
-2,42	3,49	35,74
-3,06	3,53	32,59
-3,38	3,56	31,19
-3,69	3,58	30,01
-4,30	3,60	28,47
-4,78	3,63	26,55
-5,40	3,66	24,92
-5,99	3,69	23,48

Dioda nr 3
U[V]	F[MHz]	C[pF]
-0,05	3,47	36,96
-0,23	3,70	22,64
-0,41	3,81	16,65
-0,52	3,84	15,03
-0,73	3,87	13,79
-0,94	3,88	13,16
-1,15	3,89	12,68
-1,35	3,90	12,29
-1,71	3,91	11,82
-2,01	3,92	11,44
-2,33	3,93	11,02
-2,82	3,94	10,41
-3,10	3,95	10,04
-3,64	3,96	9,31
-4,46	3,97	8,90
-4,89	3,98	8,81
-5,57	3,98	8,59
-5,90	3,98	8,54
-6,44	3,98	8,45

Całkowitą pojemność diody wyznaczę ze wzoru:

 

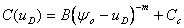
Zależność tę można zapisać w następujący sposób Y =BX^-m , wprowadzając nowe zmienne: Y=C(u_D)-C_c oraz X=ψ_o-u_D,. Po zlogarytmowaniu uzyskujemy zależność liniową:

lnY =lnB -mlnX

która pozwala na wyliczenie parametrów B i m metodą regresji liniowej funkcji w układzie współrzędnych {X,Y}. We wzorze funkcji, którą chcemy poddać regresji liniowej występują jednak 3 parametry, więc przyjmuję, że Y₀=0,9 [V].

Wzory potrzebne do wyznaczenie parametrów regresji liniowej:

 

 

 

 

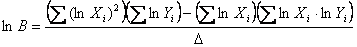
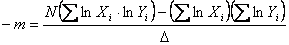
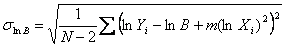
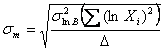
gdzie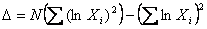  

Uzyskane wyniki:

Regresja liniowa	m	lnB	B	σm	σlnB	Rozkład domieszek:
dioda 1	0,436	3,421	30,595	0,011	0,015	skokowy
dioda 2	0,601	4,312	74,589	0,018	0,024	--
dioda 3	0,342	2,788	16,249	0,011	0,015	--

Dla pierwszej diody dla której m ≈ 0,5 rysuję wykres:

 

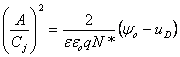
gdzie: A=1 , ε=12,3, ε₀=8,8510^-12 [F/m]

 

Z regresji liniowej wyliczonych punktów otrzymuję:

- wartość potencjału kontaktowego Y₀ [V] 

- efektywną koncentrację domieszek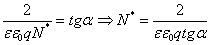  

Otrzymane wyniki:

Linia regresji wyraża się wzorem: y = 7,28*10^-4 x + 6,50*10^-4

Y₀ = 0,8667 [V] 

N* = 4,02 * 10¹²

Wnioski:

Niestety z powodu awarii komputera nie mogłem przeprowadzić pomiarów z należytą dokładnością, jednak w przypadku jednej diody udało mi się zaobserwować skokowy rozkład domieszki i związane z nim zależności. Pozostałe diody wykazują hiperskokowy rozkład domieszki. Otrzymane wyniki potwierdzają rozważania teoretyczne i pomimo awarii sprzętu przeprowadzone ćwiczenie uważam za udane.