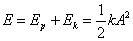Ruch, który charakteryzuje się powtarzalnością w regularnych odstępach czasu nazywa się ruchem okresowym (periodycznym). Przemieszczenie cząstki w takim ruchu w każdym momencie czasu można opisać za pomocą funkcji sinus lub cosinus. I właśnie od nazwy tych funkcji ruch ten przyjął nazwę ruchu harmonicznego.
Ruch harmoniczny odbywa się pod wpływem siły harmonicznej. Siła ta jest proporcjonalna do wychylenia ciała z położenia równowagi.
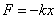
gdzie k - współczynnik sprężystości
Dla prostego oscylatora harmonicznego przemieszczenie można opisać równaniem:
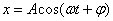
gdzie A to amplituda drgań, a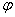 
jest dowolną stałą fazową.
Natomiast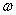 
dane jest zależnością: 
.
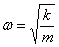Wartości funkcji sinus i cosinus powtarzają się przy każdej zmianie kąta o 2
. Można stad wnioskować na temat czasu, po którym nastąpi ta powtórka. Czas ten nazywany jest okresem drgań i dany jest wzorem:
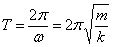
Okres drgań nie jest zależny od amplitudy drgań.
Okres drgań wahadła matematycznego czyli wyidealizowanego ciała, które ma punktową masę i zawieszone jest na nieważkiej nici można przedstawić wzorem:
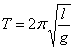
gdzie l to długość nici a g - przyspieszenie ziemskie
Innym rodzajem wahadła jest wahadło fizyczne czyli bryła sztywna, zamocowana w taki sposób, że może się wahać wokół osi, która przecina tą bryłę.
Wzór na okres drgań wygląda następująco:
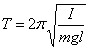
gdzie I to moment bezwładności.
Energia potencjalna w każdym momencie ruchu dana jest zależnością:
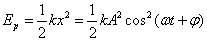
Podczas ruchu energia potencjalna zmienia się od zera do wartości maksymalnej.
Energię kinetyczną natomiast można przedstawić za pomocą zależności:
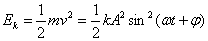
Całkowita energia mechaniczna jest sumą energii potencjalnej i kinetycznej. Jest ona proporcjonalna do kwadratu amplitudy tego ruchu.
