Wzory

POTĘGOWANIE

a ^m * a ⁿ = a ^{m + n}

a^m : a ⁿ = a ^{m - n}

(a ^m )ⁿ = a ^{m * n}

(a * b)ⁿ = a ⁿ * b ⁿ

(a/b) ⁿ = a ⁿ /b ⁿ

a ⁰ =1

WZORY SKRÓCONEGO MNOŻENIA

(a + b)² = a² + 2ab + b²

(a - b)² = a² - 2ab + b²

a² - b² = (a + b)(a - b)

(a + b)³ = a³ + 3a2b + 3ab2 + b³

(a - b)³ = a³ - 3a²b + 3ab² - b³

a³ + b³ = (a + b)(a² - ab + b²)

a³ - b³ = (a - b)(a² + ab + b²)

PIERWIASTKOWANIE

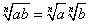
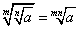
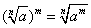
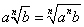
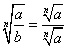
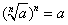
WARTOŚĆ BEZWZGLĘDNA

|x| =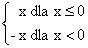

RÓWNANIA I NIERÓWNOŚCI Z WARTOŚCIĄ BEZWZGLĘDNĄ

Równanie: | x - a | = b, oznacza, że x - a = b lub x - a = - b.

Nierówność: | x - a | < b, jest spełniona wtedy i tylko wtedy gdy: x - a > - b lub x - a < b

Nierówność: |x - a| > b jest spełniona wtedy i tylko wtedy gdy: x - a < - b lub x - a > b

TRÓJMIAN KWADRATOWY

f(x) = ax²+bc+c

∆ = b² - 4ac

Jeżeli ∆ < 0, wtedy: brak miejsc zerowych

Jeżeli ∆ > 0, wtedy: dwa miejsca zerowe: x₁ = 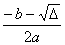 , x₂ =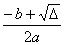 

Jeżeli ∆ = 0, wtedy: jedno miejsce zerowe: x₀ =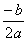 

Współrzędne wierzchołka paraboli:

W =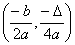

Wzory Viete'a:

x₁ + x₂ = 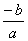 x₁ * x₂ =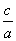 

TRYGONOMETRIA

sin 2a + cos 2a = 1

tg a × ctg a = 1

Wzory redukcyjne:

sin (90°+a) = cos a sin (180°+a) = - sin a

cos (90°+a) = -sin a cos (180°+a) = -cos a

tg (90°+a) = -ctg a tg (180°+a) = tg a

ctg (90°+a) = -tg a ctg (180°+a) = ctg a

sin (270°+a) = -cos a sin (360°+a) = sin a

cos (270°+a) = sin a cos (360°+a) = cos a

tg (270°+a) = -ctg a tg (360°+a) = tg a

ctg (270°+a) = -tg a ctg (360°+a) = ctg a

Fukncje trygonometryczne sumy kątów:

sin (a + b) = sin a cos b + cos a sin b

cos (a + b) = cos a cos b - sin a sin b

Funkcje trygonometryczne różnicy kątów:

sin (a - b) = sin a cos b - cos a sin b

cos (a - b) = cos a cos b + sin a sin b

Funkcje trygonometryczne kąta podwojonego:

sin 2a = 2 sin a cos a

cos 2a = cos²a - sin²a

Sumy funkcji trygonometrycznych:

sin a + sin b = 2 sin 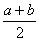 cos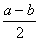

cos a + cos b = 2 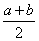cos cos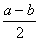

Różnice funkcji trygonometrycznych:

sin a - sin b = 2 sin 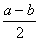 cos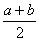

cos a - cos b = - 2 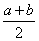sin sin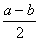

CIĄGI LICZBOWE

CIĄG ARYTMETYCZNY to ciąg liczbowy, w którym kolejny wyraz powstaje poprzez dodanie do poprzedniego ustalonej liczby r

r =a_n+1- a_n

Wyraz ogólny ciągu: a_n = a₁ + (n - 1) r

Suma częściowa:

Sn =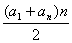 

CIĄG GEOMETRYCZNY to ciąg liczbowy, w którym kolejny wyraz powstaje poprzez pomnożenie poprzedniego wyrazu poprzez ustaloną liczbę q

q =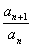 

Wyraz ogólny ciągu: a_n = a₁ × q^n-1

Suma częściowa:

S_n =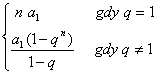 

POCHODNA

(a)' = 0

(ax + b)' = a

(ax² + bx + c) = 2ax + b

(x^a)' = a x ^a-1

= 

 =

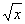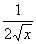
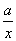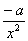
Równanie stycznej do wykresu w punkcie (x₀, y₀)

y - y₀ = f'(x₀)(x - x₀)

POLA FIGUR PŁASKICH:

trójkąt: P = 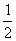a h

trójkąt równoboczny:

r =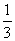h =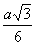

h =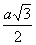 

Równoległobok: P= a h

P = a b sin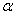

Romb: P= a h

P = a² sin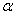 

Trapez:

P =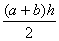 

Koło i okrąg:

Pole koła: P = 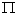r²

Obwód koła: l = 2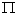r

STEREOMETRIA

Sześcian: V = a³

Prostopadłościan: V = a b h

Walec: V = 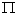r² h

Ostrosłup: V = 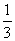P_p h

Stożek: V = 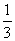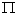r² h, S_b = 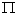r l

Kula: V = 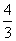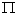r³, S = 4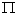r²

OKRĄG

Równanie okręgu:

(x - a)² + (y - b)² = r²

x² + y² - 2ax - 2by + c = 0

PRAWDOPODOBIEŃSTWO

Własności:

P(Ø)=0

P(A')=1 - P(A)

P(A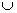B)=P(A) + P(B) - P(A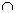B)

Permutacje: n!

Wariacje:

z powtórzeniami: n^k

bez powtórzeń: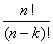

Prawdopodobieństwo warunkowe:

P (A  B) =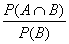 

Zdarzenie niezależne:

P(A∩B)=P(A)×P(B)