Pitagoras (ok. 572-497 p. n. e) 

Pitagoras urodził się na wyspie Samos. Gdy miał 40 lat opuścił Jonię będącą w stanie wojny z Persami, od tego czasu wiele podróżował, także do Indii. Był założycielem szkoły filozoficzno - religijnej w Krotonie oraz Związku Pitagorejskiego. Po Pitagorasie nie pozostały żadne dzieła, ale stworzył on system naukowych poglądów, które do dziś nazywamy jego imieniem. Prawdopodobnie to co przypisuje się Pitagorasowi, zostało wymyślone przez uczonych zwanych pitagorejczykami. Z literatury starogreckiej wnosimy, że Pitagoras był pierwszym, który użył określenia "miłość mądrości". Wprowadził również pojęcie dotyczące podobieństwa figur oraz pomysł a przeprowadzanie dowodów geometrycznych. Sam też przeprowadził dowód twierdzenia nazywanego dzisiaj twierdzeniem Pitagorasa.

Euklides z Aleksandrii (ok. 365 - ok. 300 p. n. e.) 

Jest autorem obowiązującego przez stulecia podręcznika "Elementy geometrii". Usystematyzował on całość starej wiedzy matematycznej. Sformułował w swoich pracach z optyki prawo załamania oraz zasadę prostoliniowego rozchodzenia się światła. Pisał również dzieła z teorii muzyki oraz z astronomii.

François Viete (1540-1603)

Z zawodu prawnik oraz autor prac z trygonometrii sferycznej oraz algebry. Wprowadził oznaczenia literowe dla stałych w równaniach oraz opracował metody rozwiązywania równań drugiego, trzeciego i czwartego stopnia. Jego imieniem są nazwane również wzory, które wiążą współczynniki równania z jego pierwiastkami

Newton Isaac Sir(1643-1727), matematyk, fizyk, filozof i astronom. Był profesorem matematyki i fizyki na Uniwersytecie w Cambridge 1669-1701. Od 1672 roku był członkiem Royal Society oraz jego prezesem od 1703, również członkiem paryskiej AN od 1699. Tytuł szlachecki otrzymał w 1705.

Philosophiae naturalis principia mathematica opublikował w 1687, sformułował w niej podstawy klasycznej fizyki (zasady dynamiki Newtona) oraz przedstawił jak je zastosować w zagadnieniach z mechaniki, fizyki i astronomii. Sformułował również prawo powszechnego ciążenia (prawo grawitacji Newtona) oraz wyjaśnił pływy morza i uzasadnił wszystkie prawa Keplera. Przyczynił się również do rozwoju optyki. Był twórcą korpuskularnej teorii budowy światła o co spierał się z Ch. Huygensem. Zajął się również określeniem zasad geometrycznej optyki i był odkrywcą interferencji światła, czyli tak zwane pierścienie Newtona. Dało to początek badaniom dotyczącym ciepła, wprowadził skalę dla stopni ciepła oraz prawo odnośnie stygnięcia ciał. Odkrył również rachunek całkowy i różniczkowy. Zaprezentował metodę jak rozwiązywać równania w sposób przybliżony metodą stycznych. Podał także interpolacyjny wzór dla n - tego stopnia wielomianu. Zajmował się badaniem własności krzywych oraz był twórcą mechanicyzmu w filozofii.

Kopernik Mikołaj (1473-1543) był wybitnym polskim astronomem, matematykiem, lekarzem, prawnikiem, tłumaczem poezji włoskiej oraz ekonomistą. Wywodzi się z krakowskiej rodziny mieszczańskiej. Urodził się w Toruniu, ale był studentem krakowskim w latach (1491-95), później w Bolonii, Padwie oraz Ferrarze. Tam też w 1503 został doktorem prawa kanonicznego. Gdy powrócił do Polski mieszkał w Lidzbarku Warmińskim. Był lekarzem i sekretarzem swojego wuja - biskupa warmińskiego - Łukasza Watzenrode.

Został kanonikiem warmińskim w 1510 po czym zamieszkał i prowadził obserwacje astronomiczne oraz pisał swoje główne dzieło we Fromborku. Gdy wybuchła wojna polsko-krzyżacka zaangażował się w obronę Olsztyna (1520-1521). Sformułował prawo, prawo Greshama-Kopernika, które mówi, że lepszy pieniądz jest wypierany przez gorszy.

Kopernik opracował teorię heliocentryczną dotyczącą modelu Układu Słonecznego. Był on oparty o trzy założenia: planety okrążają słońce torami kolistymi, Ziemia to planeta oraz obraca się dookoła własnej osi. Ten heliocentryczny model Kopernik opublikował w dziele: De revolutionibus orbium coelestium, czyli: O obrotach ciał niebieskich.

Archimedes (ok. 287-212 p. n. e)

Opracował on wzory dotyczące pola powierzchni oraz objętości kuli, czaszy kulistej, walca oraz objętości paraboloidy, elipsoidy i hiperboloidy obrotowej. Oszacował również poprawnie wartość pi i nazwał od pierwszej litery wyrazu greckiego "perimetros" co oznacza obwód koła. Również on wynalazł wielokrążek udoskonalony oraz tak zwaną śrubę Archimedesa. Konstruował machiny wojenne, które były wykorzystywane do obrony przed Rzymianami Syrakruz w latach 214-212 p. n. e., co miało miejsce podczas II wojny punickiej. Po zdobyciu miasta został zabity przez żołnierza rzymskiego.

Laplace Pierre Simon de(1749-1827), był wybitnym matematykiem, fizykiem i astronomem francuskim. Był profesorem Akademii Wojskowej w Paryżu (od 1772), członkiem AN (od 1785), dyrektorem Urzędu Miar i Wag w Paryżu (po 1790), w 1799 ministrem spraw wewnętrznych, w 1803 wiceprzewodniczącym Senatu we Francji, w 1817 dostał tytuł markiza oraz para Francji.

Był twórcą współczesnej postaci rachunku prawdopodobieństwa. Zajmował się pisaniem prac z rachunku różniczkowego, teorii wyznaczników, rachunku operatorowego (od jego nazwiska pochodzi nazwa laplasjan). Był twórcą teorii funkcji kulistych, zajął się rozwojem klasycznej mechaniki nieba oraz zaprezentował model pokazujący powstanie Układu Słonecznego. Ma swój wkład w teorii powszechnego ciążenia.

Kepler Johannes urodzony w 1571, był wybitnym astronomem, matematykiem i fizykiem niemieckim w okresie renesansu. Ten profesor na uniwersytecie w Grazu i Linzu, uczył się u Tycho de Brahe, później zaś kontynuował jego prace w obserwatorium w Pradze. Był gorącym zwolennikiem teorii Mikołaja Kopernika, był odkrywcą praw rządzących ruchem planet w Układzie Słonecznym (zwanymi teraz prawami Keplera ), publikował własne tablice astronomiczne. Zajmował się także obliczaniem objętości brył obrotowych oraz prowadzał prace związane z optyką m.in. skonstruował lunetę (zwaną lunetą keplerowską). Badał także prawo załamania światła (załamanie światła). Jako pierwszy przewidywał istnienie księżyców wokół Marsa.

Trzy prawa Keplera sformułowane przez niego, opisujące ruch planet w naszym Układzie Słonecznym:

1. Wszystkie planety krążą po orbitach w kształcie elips, których jednym z ognisk jest zawsze Słońce.

2. Każdą planetę opisuje stała wielkość jest nią tzw. prędkość polowa ( wyliczmy ją dzieląc pole powierzchni figury, jaka powstaje z łuku elipsy po jakiej porusza się planeta w jednostce czasu i odległości między końcami łuku i ogniskiem).

3. Trzecie potęgi średnich odległości między planetą a Słońcem są proporcjonalne do kwadratu okresu obiegów tych planet dookoła Słońca.

Błażej Pascal- urodzony 19 czerwca 1623 r. w mieście Clermont, zmarł w 1662 r. w Paryżu.

Pascal to znakomity francuskim filozof, matematyk, fizyk i publicysta. Powszechnie uważano go za kontynuatora myśli Kartezjusza (R. Descartes).

Był obrońcą jansenizmu oraz idei świętego Augustyna. Był również krytykiem moralności jezuickiej, co się przejawiało w Prowincjałkach (1656-1657, wydanie polskie 1921).

Jednakże jego matematyczne zainteresowania nie były ograniczone do geometrii. Napisał prace również z takich dziedzin jak: arytmetyka teoretyczna, algebra, poza tym odkrył w jaki sposób można obliczyć współczynniki Newtona. Dokonać można tego w następujący sposób, w oparciu o tak zwany trójkąt Pascala. Trójkąt ten jest utworzony z współczynników z rozwinięcia n - tej potęgi dwumianu (a+b)n. W takim trójkącie na jego ramionach występują jedynki, natomiast środek jest zapełniony liczbami, które są sumą dwóch liczb znajdujących się bezpośrednio nad nimi.

Pascal ma swój udział w tworzeniu podstaw rachunku prawdopodobieństwa oraz po części rachunku różniczkowego. Jego nazwisko można znaleźć również poza literaturą matematyczną. W fizyce sformułował wniosek wynikający z zasady Torricellego, który mówi o wysokości słupka rtęci. Jej wysokość utrzymywana przez ciśnienie powietrza jest niższa na szczytach gór niż u ich podstaw. Ponadto Pascal odkrył prawo, które również zostało nazwane jego imieniem - prawo Pascala. Mówi ono o tym, że ciśnienie wywarte na ciecz będzie się rozchodziło równomiernie wewnątrz cieczy we wszystkich możliwych kierunkach.

Pascal stał po stronie jansenizmu, który był potępiony przez papieży z reformatorskiego filozoficznego prądu we francuskim katolicyzmie, który był skierowany głównie przeciwko jezuitom. Był również propagatorem oddzielenia religii od nauki oraz wiary od rozumu.

Rozbudował on zasady metodologii i logiki. Jego wzorem wiedzy była geometria, mimo, że uważał, że nie można dzięki niej poznać nieskończoności oraz nie pomaga rozwiązać zagadnień religijnych i etycznych. Wiedział on, że geometria ułatwia poznanie faktów, jednakże nie przynosi dla nich zrozumienia, a bez niego nie można mówić o poznaniu.

Paskal nie utworzył nowej filozofii, Jego koncepcje, które zostały spisane w Myślach (1670, polski przekład 1921) to wyraz jego wewnętrznych zmagań, które wiodły od sceptycyzmu, poprzez racjonalizm, aż do mistyki.

Pascal połączył oba kroki w badaniu prawdziwości twierdzenia za pomocą indukcji matematycznej. W pierwszym kroku sprawdza się prawdziwość twierdzenia dla pierwszego elementu, czyli dla jedynki. W drugim etapie zakłada się prawdziwość twierdzenia dla liczby n i udowadnia się, że przy takim założeniu twierdzenie jest prawdziwe dla n + 1.

Leonhard (Leonard) Euler (1707-1783) został matematykiem przez przypadek. Jego ojciec był protestanckim duchownym i mieszkał koło Bazylei. Wysłał on młodego Leonarda na uniwersytet w Bazylei by ten studiował teologię. Na tymże uniwersytecie, wówczas trzynastoletni Leonard, poznał Jana Bernoulliego, po czym zaprzyjaźnił się z dwoma jego synami: Mikołajem oraz Dawidem. Mając 16 lat ukończył matematykę, a nie jak chciał ojciec teologię. Trzy lata potem dostał pierwszą nagrodę od Szwajcarskiej Akademii Nauk, napisał pracę odnośnie optymalizacji rozstawienia masztów żaglowców. Kariera naukowa Eulera spełniła się jednak na innych uniwersytetach. Caryca Katarzyna Pierwsza w 1724 roku zaczęła organizować Akademię w Sankt Petersburgu. W tej Akademii posady dostali młodzi synowie Bernoulliego, a dzięki temu, że się przyjaźnili, sprowadzili Leonarda do siebie. W tym czasie Uniwersytet w Bazylei nie powierzył katedry fizyki Eulerowi, tłumacząc to jego zbyt młodym wiekiem, ponieważ miał on wtedy 20 lat. Gdy przyjechał do Sanki Petersburga umarła Katarzyna Pierwsza i Akademia podupadła. Wtedy Leonard przyjął inna posadę - podoficera we flocie carskiej. Do Akademii wrócił po trzech latach, gdy ta zaczęła się na nowo rozwijać. Został profesorem fizyki. Po następnych trzech latach został głównym matematykiem, gdy Akademię opuścił David Bernoulli. W 1741 roku Fryderyk Wielki zaproponował Eulerowi posadę szefa matematyków w Berlińskiej Akademii. Ośrodek ten miał dużo większe znaczenie w świecie nauki niż carska Akademia. Euler przyjął ją i spędził w Berlinie 25 lat. Potem powrócił do Petersburga, ponieważ uprosiła go o to Katarzyna Wielka oraz zaoferowano mu lepsze warunki finansowe. W tym czasie popsuły się również stosunki Eulera z Fryderykiem Wielkim, więc tym chętniej opuścił Berlin.

Euler bardzo dobrze liczył a pamięć miał fenomenalną. Na początku pobytu w Sankt Petersburgu zaczął opracowywać skomplikowane astronomiczne tablice. zleceniodawcy szacowali prawdopodobny czas ukończenia pracy na kilka miesięcy. Euler ukończył je w trzy dni. Niestety zapłacił za to wielką cenę. Przypuszczalnie wyczerpany wysiłkiem dostał wysokiej gorączki, w jej wyniku stracił wzrok, na szczęście tylko w jednym oku. Niestety to szczęście w nieszczęściu nie trwało długo. Drugie oko po powrocie do Sanki Petersburga zapadło na zaćmę. Euler wydawał się tym nie przejmować, pracował dalej. Swoje książki oraz rozprawy dyktował służącym oraz swoim synom. Jeden z jego służących napisał pod Eulera dyktando sławne: ,,Kompletne wprowadzenie w algebrę'' (Vollständige Anleitung zur Algebra''), które zostało przetłumaczone na prawie wszystkie główne europejskie języki oraz zaistniało jako pierwowzór podręcznika algebry. Lista prac, które opublikowano za życie Eulera zajmowała tylko 50 stron. Do druku nadal pozostawała sterta książek, opracowań i rozpraw, która za życia Eulera rosła bardzo szybko. Pozostało ich około 700 różnorakich książek, opracowań czy rozpraw. Petersburska Akademia wydawała je jeszcze przez 50 lat po śmierci Eulera. Najważniejsze dzieła Eulera, które są fundamentalne i nie jest to przesadą to: Introductio in Analysin Infinitorum (1748), Institutiones Calculi Differentialis (1755) i Institutiones Calculi Integralis (1770). Jest to trylogia, która stanowi kompendium wiedzy matematycznej osiemnastego wieku. Pełno w tym dziele osobistych wkładów Eulera w rozwój matematyki.

Pierwszy z tomów trylogii, na który składają się dwa wielkie woluminy, stanowi o teorii funkcji, a szczególnie o funkcjach logarytmicznych, trygonometrycznych oraz wykładniczych, jak również o szeregach potęgowych, teorii liczb, geometrii analitycznej na płaszczyźnie i przestrzeni.

Dwa kolejne tomy są obszernym wykładem z analizy matematycznej.

Zasługa dzieł Eulera jest tak wielka, że oznaczenia, które stosuje dla funkcji czy wielkości matematycznych, będące jego własnymi pomysłami lub zapożyczeniami są dzisiaj uważane za "ortografię matematyczną". Jak wiadomo, Euler nie był tym, który wymyślił symbol 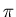 jako oznaczenie stosunku obwodu do średnicy okręgu, ale konsekwentnie go używał i zostało tak do dzisiaj.

Euler to matematyk natchniony i mało ortodoksyjny. W jego czasach odsuwano rygor matematyczny, alby tylko uzyskać ciekawy wynik.

Euler przyczynił się do powstania topologii, ponieważ rozpoczął badania, które do tego doprowadziły. Zaczęło się od zadania z mostami królewskimi.

Euler zajął się sformułowaniem wielu twierdzeń i definicji oraz wprowadzeniem licznych oznaczeń do współczesnej matematyki. Wprowadził również funkcje zespolone oraz pokazał wiązek pomiędzy funkcjami trygonometrycznymi i wykładniczą. Opracował również własności ogólne dla funkcji logarytmicznej. Zajmował się również teorią równań różniczkowych zwyczajnych oraz był pierwszym, który zdziałał coś w teorii równań różniczkowych cząstkowych. Wprowadził również szeregi trygonometryczne.

Wiele jego prac było związanych z zastosowaniem matematyki w technice, hydrodynamice oraz mechanice.

Tales z Miletu - przez ówczesnych pisarzy był uważany za "pierwszego" matematyka i astronoma. Miał wszechstronne zainteresowania oraz uzyskał wybitne osiągnięcia w wielu dziedzinach, którymi się zajmował. Mamy wiele dowodów na to, że tak było. Tales założył jońską szkołę filozofów przyrody, brał czynny udział w życiu politycznym i gospodarczym Miletu. Był człowiekiem praktycznym, podtrzymywał żywe stosunki handlowe z Egiptem, Fenicją czy Babilonią, do których eksportował cieszące się renomą tkaniny miletańskie. Dzięki temu często podróżował do tychże krajów, gdzie najprawdopodobniej poznał dokonania Egiptu i Babilonii w matematyce i astronomii. Tales posiadał wiedzę, którą potrafił praktycznie wykorzystać, czego dowodzą transakcje handlowe, których z powodzeniem dokonywał. Tales miał poglądy fizyczne, które odcinały się od uprzednich odnoszących się do powstania wszechświata oraz mitologicznej interpretacji zjawisk występujących w przyrodzie. W przekazach starożytnych pisarzy możemy znaleźć, że Tales przewidział zaćmienie słońca, które miało miejsce 28 V 585 r. p.n.e. oraz zmierzył wysokość piramidy, mierząc cień, jaki rzucała, na podstawie podobieństwa trójkątów.

Liczba pi istnieje już ponad 4 tysiące lat, ponieważ została dostrzeżona przez badaczy słynnej piramidy Cheopsa. Odkryli oni, że w jej wymiarach można zobaczyć ten symboliczny stosunek obwodu koła do jego średnicy. Otóż dzieląc połowę obwodu piramidy przy podstawie przez jej wysokość otrzymamy liczbę 3,14159 co daje nam liczbę pi z dokładnością do 5 cyfr po przecinku.

Najsłynniejszym twierdzeniem nazwanym imieniem Talesa jest twierdzenie o proporcjonalności odcinków w kącie przeciętym dwoma równoległymi prostymi. W czasach współczesnych Talesowi to twierdzenie nie było przewrotem, ponieważ matematyka egipska i babilońska stała na wysokim poziomie. Wielkość jaką przypisujemy Talesowi w matematyce nie wiąże się z autorstwem twierdzeń, ale głównie z pojęciem ich dowodu. Wśród matematyków egipskich i babilońskich najbardziej interesująca była wiedza "jak", natomiast Tales jako pierwszy zaczął zadawać pytanie "dlaczego". Talesa uznaje się za tego, który połączył teorię z praktyką i zbudował podstawę geometrii jako nauki dedukcyjnej, na której zbudowano Elementy Euklidesa.