- Wiadomości wstępne.
Model wielorównaniowy jest modelem zawierającym co najmniej dwa równania, przy czym co najmniej jedno równanie musi być stochastyczne, czyli musi zawierać składnik losowy.
- Klasyfikacja zmiennych
Podobnie jak w modelach jednorównaniowych, mamy zmienne objaśniane i objaśniające. W pojedynczym równaniu mamy jedna zmienną objaśnianą. Zapisujemy ją zwykle po lewej stronie równania. Natomiast po jego prawej stronie znajdują się zmienne wyjaśniające kształtowanie się zmiennej objaśnianej.
W modelach wielorównaniowych zmienne dzieli się na zmienne endogeniczne i zmienne egzogeniczne. Zmienne wyjaśniane przez model nazywają się zmiennymi endogenicznymi, natomiast zmienne egzogeniczne to takie, których wartości są określane poza modelem, dołącza się do nich zmienna odpowiadająco stałej.
Następne kryterium klasyfikacji zmiennych dotyczy sytuacji, gdy mamy wielorównaniowy model dynamiczny, gdzie występują zmienne z różnych okresów. Zmienne endogeniczne i egzogeniczne mogą być opóźnione i nieopóźnione w czasie. Zmienne nieopóźnione odnoszą się do bieżących okresów, a zmienne opóźnione do wcześniejszych okresów.
Zmienne endogeniczne nieopóźnione nazywa się zazwyczaj zmiennymi łączenie współbieżnymi. Zmienne endogeniczne opóźnione w czasie oraz zmienne egzogeniczne opóźnione i nieopóźnione określamy jako zmienne z góry ustalone. Podział ten jest ważny z punktu widzenia szacowania parametrów modelu.
- Postać strukturalna i zredukowana modelu
Poszczególne równania modelu określają relacje między zmiennymi. Model wielorównaniowy jest zatem opisem struktury układu relacji. Dlatego w literaturze ekonometrycznej taki zapis modelu wielorównaniowego, który przedstawia rzeczywiste relacje pomiędzy zmiennymi, nazywa się postacią strukturalna modelu. Aby formalnie określić, co przez to rozumiemy, oznaczmy: yit - obserwacja i-tej zmiennej endogenicznej w okresie t ,i = 1,2,…,m; zjt - obserwacja j-tej zmiennej z góry ustalonej w okresie t, j=1,2,…,k; βil - parametr przy l-tej nieopóźnionej zmiennej endogenicznej w i-tym równaniu, l, i=1,2,….,m; γij - parametr przy j-tej zmiennej z góry ustalonej w i-tym równaniu, i=1,2,…,m ; j= 1,2,…,k.
Jeżeli mamy model składający się z m równań:
y1t = 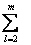 β1lylt+
β1lylt+ 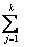 γ1jzjt+ε1t,
γ1jzjt+ε1t,
y2t = 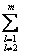 β2lylt+
β2lylt+ 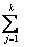 γ2jzjt+ε2t,
γ2jzjt+ε2t,
…………………..
ymt = 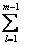 βmlylt+
βmlylt+ 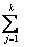 γmjzjt+εmt,
γmjzjt+εmt,
To przenosząc wszystkie zmienne łącznie współzależne i zmienne z góry ustalone na lewą stronę równań, otrzymując postać strukturalne modelu:
y1t - 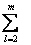 β1lylt -
β1lylt -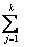 γ1jzjt=ε1t,
γ1jzjt=ε1t,
y2t - 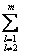 β2lylt-
β2lylt- 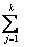 γ2jzjt=ε2t,
γ2jzjt=ε2t,
…………………..
ymt - 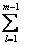 βmlylt-
βmlylt- 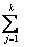 γmjzjt=εmt,
γmjzjt=εmt,
Poszczególne równania postaci strukturalnej modelu nazywamy równaniami strukturalnymi. Postać strukturalna modelu będziemy przedstawiać, używając zapisu macierzowego:
BYt+ҐZt=εt, t=1,2,…,n,
Gdzie: B - macierz parametrów przy nieopóźnionych zmiennych endogenicznych:
B= 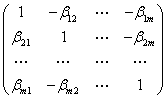
Ґ - macierz parametrów przy zmiennych z góry ustalonych:
Ґ= 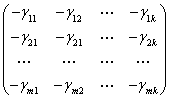
Yt - wektor obserwacji nieopóźnionych zmiennych endogenicznych w okresie t:
Yt= 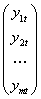
Zt - wektor obserwacji zmiennych z góry ustalonych w okresie t:
Zt=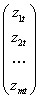
εt - wektor składników losowych w okresie t:
εt= 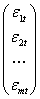
Do estymacji parametrów niektórych typów modeli konieczne jest wprowadzenie pojęcia postaci zredukowanej modelu. W postaci zredukowanej zmiennymi objaśniającymi są jedynie zmienne z góry ustalone. Aby można było przejść od postaci strukturalnej do postaci zredukowanej modelu, macierz parametrów przy zmiennych łącznie współzależnych B musi być nieosobliwa. Wówczas bowiem istnieje macierz do niej odwrotna B-1 . Mnożąc BYt+ҐZt=εt lewostronnie przez B-1 , otrzymujemy:
B-1BYt+ B-1ҐZt= B-1εt
B-1B=I , zatem powyższą zależność możemy zapisać jako:
Yt =--B-1ҐZt +B-1εt
Oznaczając Π=--B-1Ґ i ηt= B-1εt , otrzymujemy postać zredukowaną modelu:
Yt = ΠZt+ ηt
Elementy macierzy Π oznaczamy jako πij, i=1,2,…,m j=1,2,…,k, mamy zatem:
y1t = π11z1t+π12z1t+…+π1kzkt+η1t,
y1t = π21z1t+π22z2t+…+π2kzkt+η2t,
…………………………
y1t = πm1z1t+πm2zmt+…+πmkzkt+ηmt,
W postaci zredukowanej modelu nieopóźnione zmienne endogeniczne są objaśniane przez zmienne z góry ustalone.
- Klasyfikacja modeli wielorównaniowych
Ze względu na powiązania między nieopóźnionymi w czasie zmiennymi endogenicznymi modele wielorównaniowe dzieli się na modele proste, rekurencyjne i modele o równaniach współzależnych. Klasyfikację modeli wielorównaniowych przeprowadza się na podstawie macierzy parametrów strukturalnych przy nieopóźnionych zmiennych endogenicznych. Rozważa się zatem macierz B postaci strukturalnej B Yt + ҐZt= εt .
Model jest modelem prostym, jeżeli B jest macierzą jednostkową:
B= 
modelem rekurencyjnym, jeżeli B jest macierzą trójkątną:
B=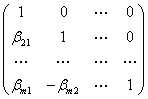
lub daje się sprowadzić do macierzy trójkątnej po odpowiednim przenumerowaniu zmiennych endogenicznych, oraz modelem o równaniach współzależnych, jeśli ni jest modelem prostym ani rekurencyjnym. W modelu prostym żadna nieopóźnione zmienna endogeniczna nie występuje w charakterze zmiennej objaśniającej w żadnym równaniu.
- Problem identyfikacji
Na podstawie zaprezentowanego wcześniej sposobu przejścia od postaci strukturalnej do postaci zredukowanej modelu stwierdzamy, że jeśli macierz B jest macierzą nieosobliwą, to zawsze można wyznaczyć macierz Π ze wzoru Π=--B Ґ. Zadani odwrotne jest znacznie trudniejsze. Polega na rozwiązaniu układu równań B Π=-- Ґ, czyli wyznaczeniu elementów macierzy B i Ґ. W ogólnym przypadku macierz B ma m2-m, a macierz Ґ ma m*k nieznanych elementów, równań zaś jest m. Nie zawsze zatem na podstawie parametrów postaci zredukowanej modelu można określić parametry postaci strukturalnej. Przedstawione zagadnienie nazywane jest problemem identyfikacji.
Model jest identyfikowalny, jeśli na podstawie parametrów postaci zredukowanej można wyznaczyć wszystkie parametry postaci strukturalnej.
Oprócz identyfikowalności całego modelu będziemy rozważać identyfikowalność poszczególnych jego równań strukturalnych. Dane równanie strukturalne jest identyfikowalne, jeśli wszystkie parametry można wyznaczyć na podstawie znajomości postaci zredukowanej. Oczywiście model jest identyfikowalny, gdy każde równanie strukturalne jest identyfikowalne.
W problemie identyfikacji mogą wystąpić trzy sytuacji:
1. Nie jest możliwe wyznaczenie wszystkich parametrów równania strukturalnego na podstawie znajomości parametrów postaci zredukowanej modelu. Równanie jest wówczas nieidentyfikowalne.
2. Na podstawie znajomości parametrów postaci zredukowanej modelu można w sposób jednoznaczny określić parametry równania strukturalnego. Równanie nazywamy wówczas jednoznacznie identyfikowalnym.
3. Jeśli parametry równania strukturalnego można wyznaczyć na podstawie parametrów postaci zredukowanej w sposób niejednoznaczny, to mówimy o równaniu niejednoznacznie identyfikowalnym.
Problem identyfikacji sprowadza się zatem do rozstrzygnięcia, czy układ równań B Π=-- Ґ ma rozwiązanie. Układ ten możne być zapisany jako:
 .
. =
=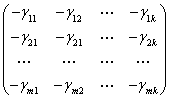
Weźmy pod uwagę i-ty wiersz macierzy Ґ. Oznaczenia: m1-liczba nieopóźnionych zmiennych endogenicznych występujących w i-tym równaniu postaci strukturalnej modelu, wyłączając yit; m2-liczba pozostałych zmiennych Endogenicznych występujących w modelu; k1-liczba zmiennych z góry ustalonych występujących w badanym równaniu; k2-liczba pozostałych zmiennych z góry ustalonych występujących w modelu. Mamy zatem zależności: 1+m1+m2=m oraz k1+k2=k, gdzie m jest liczba wszystkich nieopóźnionych zmiennych endogenicznych, a k liczba wszystkich zmiennych z góry ustalonych występujących w modelu.
Aby można było wyznaczyć parametry w i-tym równaniu postaci strukturalnej modelu, poszczególnym elementom i-tego wiersza macierzy B Π musza być równe poszczególnym elementom i-tego wiersza macierzy Ґ. mamy wiec k równań, gdyż wszystkich elementów i-tego wiersza macierzy Ґ jest k oraz m1+k1 niewiadomych, ponieważ w i-tym równaniu strukturalnym występuje m1 nieznanych elementów i-tego wiersza macierzy B oraz k1 nieznanych elementów i-tego wiersza macierzy B oraz k1 nieznanych elementów i-tego wiersza macierzy B oraz k1 nieznanych elementów i-tego wiersza macierzy Ґ.
Aby można było określić rozwiązanie, liczba równań powinna być większa bądź równa liczbie niewiadomych: k ≤ k1+k2. Zatem uwzględniając zależność k = k1+k2 otrzymaliśmy ze wymaganym warunkiem jest k2 ≥ m1.
Uzyskany wynik znany jest w literaturze ekonometrycznej jako warunek wymiaru. Można go sformułować w następujący sposób:
Warunkiem koniecznym identyfikowalności danego równania strukturalnego jest, by liczba zmiennych z góry ustalonych w modelu niewystępujących w tym równaniu była większa bądź równa liczbie nieopóźnionych zmiennych endogenicznych występujących w tym równaniu pomniejszonej o jeden.
Dodając m2 do obu stron nierówności k2 ≥ m1 otrzymujemy m2 + k2 ≥ m-1
Wniosek wymiaru może być sformułowany w równoważnej postaci:
Warunkiem koniecznym identyfikowalności danego równania strukturalnego jest, by liczba zmiennych(łącznie współzależnych i z góry ustalonych) niewystępujących w tym równaniu była większa bądź równa ogólnej liczbie nieopóźnionych zmiennych endogenicznych, pomniejszonej o jeden.
W przypadku gdy k2=m , równanie może być jednoznacznie identyfikowalne, natomiast jeśli k2>m1, jest ono niejednoznacznie identyfikowalne.
Warunkiem wymiaru jest warunkiem koniecznym, ale nie wystarczającym. Aby równanie strukturalne modelu było identyfikowalne, musi zachodzić warunek wymiaru. Natomiast może się zdarzyć, że mimo spełnienia warunku wymiaru równanie nie jest identyfikowalne.
W literaturze warunek konieczny i dostateczny identyfikowalności nosi nazwę warunku rzędu. Warunek ten wymaga zbadania rzędu odpowiedniej podmacierzy Π. Warunek konieczny i dostateczny może być sformułowany w postaci:
Warunkiem koniecznym i dostatecznym do tego, aby i-te równanie modelu składającego się z m równań było identyfikowalne, jest, by macierz utworzona z parametrów znajdujących się przy zmiennych, które są w modelu, ale nie występują w i-tym równaniu, była rzędu m-1.
- Pośrednia metoda najmniejszych kwadratów
Pośrednia metoda najmniejszych kwadratów ma zastosowanie do szacowania parametrów modeli o równaniach współzależnych jednoznacznie identyfikowalnych. Idea polega na wykorzystaniu ocen parametrów postaci zredukowanej do uzyskania ocen parametrów postaci strukturalnej.
Procedura pośredniej metody największych kwadratów jest następująca:
1. Sprowadzamy model do postaci zredukowanej:
Y = ΠZ+ η
2. Parametry postaci zredukowanej szacujemy klasyczną metodą najmniejszych kwadratów korzystając ze wzoru:
P = (ZT Z) -1 ZT Y
gdzie:
PT = 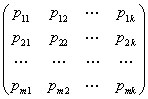
ocena macierzy Π parametrów postaci zredukowanej
Z = 
macierz obserwacji zmiennych ustalonych występujących w modelu
Y = 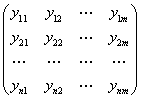
macierz obserwacji zmiennych łącznie współzależnych występujących w modelu
3. Oceny parametrów postaci strukturalnej uzyskuje się w drodze rozwiązaniu układu równań
B PT = - Ґ
PRZYKŁAD 1
Rozpatrzymy model opisujący zależność między wartością majątku trwałego w mln zł (K), zatrudnieniem w tys. Osób (Z), nakładami inwestycyjnymi w mln zł (I) i produkcją w tys. Szt. (P) o postaci:
K = 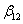 Z +
Z +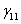 I +
I + 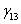 X + ε1
X + ε1
Z = 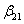 K +
K +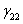 P +
P + 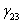 X + ε2
X + ε2
W modelu tym X jest zmienną przyjmującą wartości równe jedności.
Obserwacje poszczególnych zmiennych w siedmiu kolejnych latach są podane w poniższej tabeli:
|
t
|
kt
|
zt
|
it
|
pt
|
xt
|
|
1
|
60
|
3,4
|
1,1
|
22
|
1
|
|
2
|
62
|
3,5
|
1,5
|
24
|
1
|
|
3
|
65
|
3,7
|
1,4
|
25
|
1
|
|
4
|
66
|
3,7
|
1,7
|
28
|
1
|
|
5
|
68
|
3,9
|
1,7
|
29
|
1
|
|
6
|
69
|
4,1
|
1,9
|
33
|
1
|
|
7
|
72
|
4,1
|
1,6
|
32
|
1
|
Postać zredukowana szacowanego modelu jest następująca:
K = п11 I + п12 P + п13 X +η1
Z = п21 I + п22 P + п23 X +η2
Najpierw szacujemy klasyczną metodą najmniejszych kwadratów parametry postaci zredukowanej dla obu równań jednocześnie. Macierz obserwacji zmiennych łącznie współzależnych modelu oraz macierz obserwacji zmiennych z góry ustalonych wyglądają następująco:
Y = 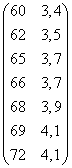 Z =
Z = 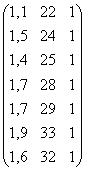
Wykonując kolejne obliczenia zgodnie ze wzorem P = (ZT Z) -1 ZT Y otrzymamy:
ZT Z = 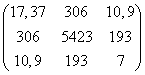
(ZT Z) -1 = 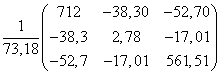
ZT Y = 
P = 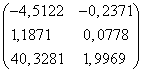
Macierz PT wartości parametrów postaci zredukowanej szacowanego modelu ma postać:
PT = 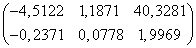
Stąd model zredukowany po oszacowaniu ma postać:
K = -4,5122 I + 1,1871 P + 40,3281 X
Z = -0,2371 I + 0,0778 P + 1,9969 X
Macierz B parametrów przy zmiennych endogenicznych bez opóźnień czasowych K i Z oraz macierz Ґ parametrów przy zmiennych z góry ustalonych I, P i X w postaci strukturalnej są następujące:
B = 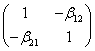 Ґ =
Ґ = 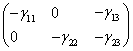
 Wobec tego układ równań B PT = - Ґ przyjmuje postać:
Wobec tego układ równań B PT = - Ґ przyjmuje postać:
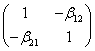
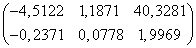 =
= 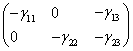
Po wykonaniu odpowiednich działań na macierzach otrzymujemy następujące układy równań:
-4,5122 + 0,2371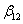 =
= 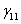
1,1871 - 0,0778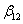 = 0
= 0
40,3281 - 1,9969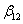 =
= 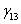
oraz
4,5122 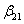 +0,2371 = 0
+0,2371 = 0
-1,1871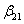 + 0,0778 =
+ 0,0778 = 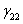
-40,328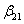 +1,9969 =
+1,9969 = 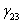
Z pierwszego równania otrzymujemy:
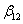 = 15,2584
= 15,2584 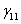 = -0,8944
= -0,8944 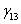 = 9,8586
= 9,8586
Z drugiego:
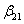 = 0,0525
= 0,0525 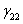 = 0,0155
= 0,0155 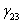 = 0,1203
= 0,1203
Ostatecznie oszacowany model przedstawia się następująco:
K = 15,2584 Z - 0,8944 I + 9,8586
Z = 0,0525 K + 0,0155 P + 0,1203
PRZYKŁAD 2
Zbudowano następujący model o równaniach współzależnych:
Pt = 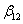 Zt +
Zt +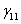 St +
St + 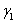 + ε1
+ ε1
Zt = 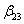 Kt +
Kt + 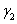 + ε2
+ ε2
Kt = 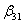 Zt +
Zt +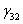 It +
It + 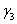 + ε1
+ ε1
gdzie:
P - produkcja w tys. szt.
Z - zatrudnienie w tys. Osób
K - wartość majątku trwałego w mln zł
S - zużycie surowca w tys. Ton
I - nakłady inwestycyjne w mld zł
Obserwacje z kolejnych 11 lat podane zostały w poniższej tabeli:
|
t
|
pt
|
zt
|
kt
|
st
|
it
|
|
1
|
46
|
3,4
|
24
|
2,3
|
1,0
|
|
2
|
48
|
3,4
|
25
|
2,4
|
1,1
|
|
3
|
49
|
3,5
|
25
|
3,2
|
1,1
|
|
4
|
52
|
3,7
|
26
|
3,4
|
1,0
|
|
5
|
52
|
3,8
|
27
|
3,4
|
1,1
|
|
6
|
54
|
3,8
|
27
|
3,4
|
1,2
|
|
7
|
57
|
3,9
|
28
|
3,3
|
1,1
|
|
8
|
59
|
4,0
|
29
|
3,4
|
1,3
|
|
9
|
59
|
4,3
|
31
|
3,5
|
1,5
|
|
10
|
60
|
4,5
|
33
|
3,5
|
1,6
|
|
11
|
61
|
4,8
|
35
|
3,6
|
1,7
|
Równania pierwsze i trzecie są jednoznacznie identyfikowalne, a równanie drugie niejednoznacznie identyfikowalne.
Postać zredukowana modelu po oszacowaniu parametrów klasyczną metodą najmniejszych kwadratów jest następująca:
Pt = 5,7338 St + 11,8721 It + 20,9805
Zt = 0,2888 St + 1,4339 It + 1,1991
Kt = 1,6339 St + 11,9946 It + 7,9565
Wyznaczamy wartości ocen parametrów strukturalnych pierwszego i trzeciego równania modelu pierwotnego. Otrzymujemy następujący układ równań:
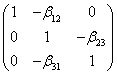
 =
= 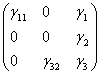
Dla pierwszego równania mamy układ równań:
5,7338 - 0,2888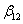 =
= 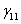
11,8721 - 1,4339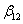 = 0
= 0
20,9805 - 1,1991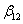 =
= 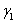
Po rozwiązaniu tego układu mamy:
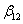 = 8,2796
= 8,2796 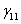 = 3,3427
= 3,3427 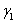 = 11,0524
= 11,0524
Dla trzeciego równania postaci strukturalnej mamy poniższy układ równań:
-0,2888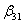 + 1,6339 = 0
+ 1,6339 = 0
-1,4339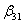 + 11,9946 =
+ 11,9946 = 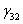
-1,1991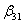 + 7,9565 =
+ 7,9565 = 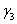
Stąd otrzymujemy:
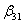 = 5,6576
= 5,6576 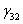 = 3,7720
= 3,7720 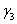 = 1,1726
= 1,1726
Z powyższych wyliczeń wynika postać równań:
Pt = 8,2796 Zt +3,3427 St + 11,0524
Kt = 5,6576 Zt +3,7720 It + 1,1726
7. Teoria konsumenta - systemy wydatków
Teoria konsumenta znana z mikroekonomii wyjaśnia sposób wydatkowania dochodu na zakup dóbr i usług za pomocą modelu behawioralnego, zakładającego, że preferencje konsumenta odzwierciedlają funkcje użyteczności oraz że w optymalnym planie konsumpcji maksymalizujemy użyteczność przy spełnieniu ograniczenia budżetowego.
Aby to zobrazować, załóżmy, że mamy D dóbr, które mają dodatnie ceny p=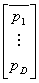 oraz zbiór możliwych planów konsumpcji q=
oraz zbiór możliwych planów konsumpcji q=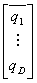 oznaczymy jako Q. Wtedy optymalny plan konsumpcji q*=
oznaczymy jako Q. Wtedy optymalny plan konsumpcji q*=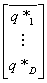 przy dochodzi m>0 musi spełniać warunki:
przy dochodzi m>0 musi spełniać warunki:
U(q*) = max u(q) dla q є Q
pTq* = m
gdzie u(q) jest funkcją użyteczności dla planu konsumpcji q. Rozwiązaniem tego zagadnienia optymalizacyjnego jest układ D funkcji popytu:
qj*(m;p1,…,pD), j=1,…,D,
przedstawiających optymalną konsumpcję D dóbr przy danych cenach p1,…,pD i danym dochodzie m. Popytowi qj*(m;p1,…,pD) odpowiada optymalny wydatek pieniężny:
wj*(m;p1,…,pD)= pjqj*(m;p1,…,pD)
W modelu D równaniowym trzeba uwzględnić błędy pomiarów wydatków lub niedoskonałą alokacje dochodów, dzięki czemu uzyskujemy poniższy model D-równaniowy:
yt1 = W1*(mt; p t1,…,p tD)+ ξt1
………………………………..
ytD = WD*(mt; p t1,…,p tD)+ ξtD
gdzie t oznacza numer obserwacji, yt = [y t1… y tD] jest t-tym zaobserwowanym wektorem wydatków na wszystkie D dóbr, natomiast ξ tj są składnikami losowymi reprezentującymi błędy alokacji dochodu i pomiaru wydatków.
PRZYKŁAD: Liniowy system wydatków
Załóżmy, że preferencje konsumentów charakteryzuje tzw. funkcja użyteczności Stone'a - Geary'ego:
u(q) =  (qj - μj)δj, gdzie qj > μj ≥ 0, μj jest niezbędnym zakupem j-tego dobra, δj > 0 (j=1,…,D) oraz
(qj - μj)δj, gdzie qj > μj ≥ 0, μj jest niezbędnym zakupem j-tego dobra, δj > 0 (j=1,…,D) oraz 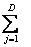 δj = 1. Powyższa funkcja użyteczności prowadzi do następującego D - równaniowego modelu wydatków:
δj = 1. Powyższa funkcja użyteczności prowadzi do następującego D - równaniowego modelu wydatków:
yt1 = μ1 p t1 + δ1 (mt -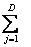 μj ptj )+ ξt1
μj ptj )+ ξt1
………………………………..
ytD = μD p tD + δD (mt -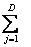 μj ptj )+ ξtD
μj ptj )+ ξtD
gdzie μj p tj jest niezbędnym wydatkiem na j-te dobro (j = 1,…,D), różnica w nawiasie jest tzw. funduszem swobodnej decyzji, czyli tą częścią dochodu, która pozostaje po dokonaniu wszystkich niezbędnych wydatków, δj jest interpretowane jako udział wydatków na j-te dobro w funduszu swobodnej decyzji.
Wydatki pojedynczego konsumenta są uzależnione od jego dochodu oraz od cen dóbr, natomiast te wydatki nie mają wpływu na poziom dochodu i cen.
W modelu liniowego systemu wydatków wydatki są liniowo zależne od zmiennych egzogenicznych, stąd jego nazwa.
Liniowy system wydatków można przedstawić w zapisie macierzowym jako:
yt + xtΓ= ξ t
gdzie:
yt = [ y t1 y t2 … y tD ]
xt = [ p t1 p t2 … p tD m t]
ξt = [ξ t 1 ξ t 2 … ξ t D ]

 (δ1 -1) μ1 δ2 μ1 … δD μ1
(δ1 -1) μ1 δ2 μ1 … δD μ1
δ1 μ2 (δ2 -1) μ2 … δD μ2
Γ = ………………………….
δ1 μD δ2 μD … (δD -1) μD
-δ1 -δ2 … -δD
Przy estymacji ,modelu należy pamiętać, że:
1) macierz Γ o wymiarach (D+1) x D, ma (D+1)D elementów, które są funkcjami zaledwie 2D - 1 swobodnych parametrów strukturalnych μ1, … , μD, δ1, …, δD-1
(δD = 1- δ1 - … - δD-1)
2) aby ograniczenie budżetowe [ yt1 + … + y tD = m t było spełnione, składniki losowe poszczególnych równań muszą sumować się do zera: ξ t 1 +… + ξ t D = 0, czyli muszą być liniowo zależne.


