Spis treści:
Ciekawa zagadka matematyczna. Ćwiczy wyobraźnię!
Zagadka wymaga znajomości podstawowego twierdzenia matematycznego, jednak to wcale nie największy problem. Żeby wpaść na metodę rozwiązania, musisz użyć wyobraźni i zwizualizować sobie całą sytuację. Musisz też wyłuskać sedno problemu nie zwracając oddzielając kluczowe dane od nieistotnych fragmentów polecenia. Przeczytaj je uważnie:
Niedaleko brzegu niewielkiego, malowniczego jeziorka, w którym tłoczno od łabędzi i żurawi rosła samotna trzcina. Jej wierzchołek wystawał pół łokcia nad powierzchnię wody. Gdy nad akwenem zerwał się silny, jednostajny wiatr, łodyga zaczęła chylić się i zanurzać, aż w końcu jej końcówka zniknęła pod wodą dwa łokcie od miejsca, gdzie jeszcze przed chwilą wyłaniała się z toni.
Jaką głębokość miała woda w tym punkcie jeziorze?
Czy masz już w głowie schemat z przebiegiem całego zdarzenia? Właśnie tego potrzebujesz, do rozwiązania zagadki.
Rozwiązanie zagadki. Wykorzystaj to twierdzenie
Spokojnie przeanalizujmy całe polecenie. Trzcina wyrasta z dna jeziora i wznosi się pionowo w górę. Jej czubek przy bezwietrznej pogodzie wystaje ponad wodę na pół łokcia. Wiatr działa na fragment łodygi nad powierzchnią, jednak ten nie odłamuje się – przechył dotyczy całej rośliny. Wierzchołek znika dwa łokcie od miejsca, w którym wcześniej łodyga przebijała lustro jeziora. W tym momencie łodyga jest jednocześnie prostą łączącą dno jeziora z powierzchnią wody.
Intuicja powinna już nam podpowiadać, że w poleceniu ukryte są długości pewnych odcinków, a ruch łodygi pod wpływem wiatru i lustro wody tworzą układ prostych. W nim rysuje się dobrze znany nam wszystkim wariant trójkąta – trójkąt prostokątny.
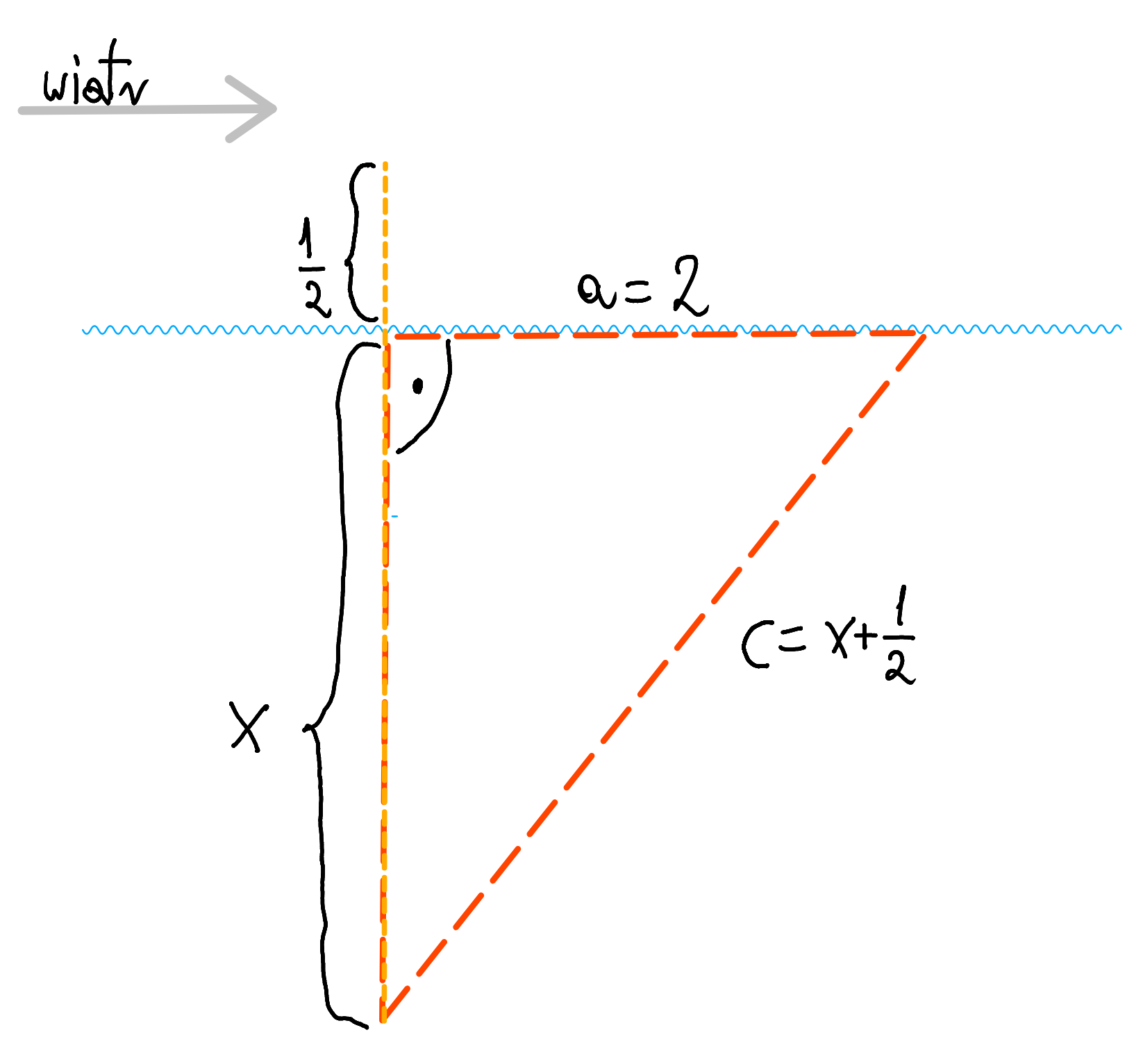
Teraz widać już dobrze, że do rozwiązania zagadki konieczne jest skorzystanie z twierdzenia Pitagorasa.
Jak na tacy podaną mamy długość jednej z przyprostokątnych – 2 łokcie odcinka na lustrze jeziora. Druga przyprostokątna to szukany przez nas x. Długość przeciwprostokątnej to x + 0,5 łokcia z początku wystającego nad powierzchnię wody.
Dla pełnej jasności przypomnijmy twierdzenie Pitagorasa:
c2 = a2 + b2
Teraz podstawmy dane:
(x + 0,5)2 = x2 + 22
x2 + x + 0,25 = x2 + 4
Po przeniesieniu wyrażeń na właściwe strony okazuje się, że kwadraty uległy skróceniu, a nam zostaje:
x = 3,75
Głębokość wody, w miejscu, z którego wyrasta nasza trzcina wynosi 3,75 łokcia.
Źródła: math.edu.pl; bryk.pl
Rozwiąż inne zagadki Bryka:
Zagadka ze stadem gęsi. Wystarczy wiedza z podstawówki
Zagadka o leniwym ogrodniku. Wystarczy logicznie pomyśleć
Zagadka na logiczne myślenie. Sprawdź, czy podołasz wyzwaniu
Zagadka dla sprytnych. Ile wynosi suma sumy z sumy cyfr liczby 3583?


