Jak wiadomo liczba oraz figury geometryczne powstały dużo wcześniej niż teksty matematyczne. Najstarsze teksty matematyczne, jakie zostały napisane i znamy je do dzisiaj, pochodzą z drugiego tysiąclecia p. n. e. z jego początku. W tym właśnie okresie rozkwitały dwie wielkie cywilizacje na starożytnym Wschodzie, mowa o Babilonie oraz Egipcie.
Starożytny Egipt (IV tysiąclecie p.n.e. - 641 n. e.), był krajem, który miał wyraźnie wytyczne granice. Na zachodzie były one położone na Saharze od wschodu i północy tworzyły ją Morze Śródziemne oraz Morze Czerwone natomiast południową granicę stanowił skalisty Punt, na pograniczu Sudanu i Etiopii. Dzięki takiemu położeniu geograficznemu, Egipt był mniejszym stopniu narażony na obce najazdy. Nil, który systematycznie wylewał, wpływał na płodność gleby przez co umożliwiał na tych terenach wysoki poziom oraz rozwój rolnictwa. Właśnie z tego powodu życie starożytnego Egiptu było skupione w przeważającym stopniu wzdłuż nad rzeką. W owych czasach było tam największe skupisko ludności, dlatego organizacja państwa, była tym c było w Egipcie bardziej potrzebne niż w innych miejscach.
W Egipskim państwie na jego czele stał faraon czyli "bóg o władzy absolutnej" jak mówiła religia starożytnego Egiptu. Państwem rządzili urzędnicy natomiast chłopi uprawiali ziemię. Władcy Egiptu prowadzili liczne wojny, ale kraj w pokoju się rozwijał. Egipska ludność była zrzeszona w brygady kilkudziesięcioosobowe, które nie miały stałego miejsca pobytu. Byli oni bardzo dyspozycyjni więc państwo mogło podejmować nawet bardzo ambitne przedsięwzięcia. Były prowadzone duże publiczne roboty, które dawały zatrudnienie licznym robotnikom. Należały do nich na przykład piramidy w Gizie czy Sakkara. Najbardziej znane budowle to piramida Dżerseja (pierwsza), powstała ona koło 2650 r. p. n. e. oraz piramida Cheopsa, którą wybudowano prawie sto lat później.
Wyprawy do Libii i na Synaj sprawiły, że wzrosła ilość kupców i rzemieślników. Dzięki temu zaczęły się rozwijać też nauki: matematyka, przy czym szczególnie geometria oraz miernictwo, astronomia, która rozwinęła się ponieważ przydatne było określenie, kiedy będzie wylew Nilu, czy do kreślenia map nieba. Rozwijała się również medycyna, szczególnie chirurgia, ziołolecznictwo oraz mechanika i technika, ponieważ przydatna była w budownictwie czy przy irygacji oraz literatura.
Historia Państwa Starego jest nam znana tylko w zarysie. Tu i ówdzie możemy znaleźć jakieś informacje o powstaniu czy rozwoju różnorodnych dziedzin nauki. O matematyce Wczesnego oraz Starego Państwa wiemy bardzo mało. Do dzisiaj zachowały się jedynie zapisy liczbowe lub rysunki na płytach oraz ścianach kamiennych. Natomiast teksty matematyczne, które przetrwały w starożytnych zabytkach zostały napisane na papirusie, który był wyrabiany z łodygi papirusu. Podstawowe informacje jakie posiadamy o matematyce staroegipskiej pochodzą tylko z jednego okresu i nie da się stwierdzić jak się ona rozwijała w przeciągu swoich dziejów. Pomimo to naukowcy zdołali pogłębić wiadomości o liczbach egipskich. Sposób w jaki przydzielano ziemię brygadom do obróbki pokazuje nam, że znano w tamtych czasach pojęcie gabarytu. Wzór do liczenia objętości, czyli pole podstawy razy wysokość, uznawano za odpowiedni dla prostokąta, jak również dla trójkąta. Piśmiennictwo starożytnego Egiptu rozwinęło się po wynalezieniu pisma ideograficznego, czyli takiego, w którym pojęciom odpowiadały odpowiednie obrazki czyli hieroglify. Takie pismo wykluczało system pozycyjny. Nie zajmowano by się egipskim pismem, ponieważ było ono prymitywniejsze od babilońskiego, gdyby nie fakt, że dzięki niemu rozwinęła się arytmetyka. Poprzez dorysowywanie owali nad lub obok hieroglifu, które oznaczały liczbę, oznaczało, że trzeba było go odczytywać inaczej – jako odwrotność. Inaczej mówiąc owal oznaczał to samo w starożytnym Egipcie co dzisiaj wykładnik -1.
Znaki egipskie były ryte lub rzeźbione dłutem oraz młotkiem na pomnikach kamiennych lub rysowane na skalnych odłamkach, skorupach garnków czy liściach papirusu przy pomocy trzciny, która miała zgnieciony koniec, który maczano w barwniku.
W starożytnym Egipcie znane i stosowane były wielkie liczby. System numeracji, jakiego wtedy używano pozwalał na wyrażenie liczb, które przekraczały milion. Specjalne hieroglify oznaczały jedności oraz kolejne potęgi liczby dziesięć, włącznie do siódmej.
W Hierakonpolis, w starożytnym mieście położony po lewej stronie Nilu miej więcej 100 km za pierwszą kataraktą, została znaleziona buława z paroma napisami. Jest ona najstarszym znanym świadectwem archeologicznym dotyczącym pisma oraz numeracji egipskiej. Wspomniana buława należała do Namera, król ten zjednoczył Górny i Dolny Egipt koło 2900 r. p. n. e. Poza imieniem Narmera, które było zapisane fonetycznie, na buławie, na jej głowie, zapisane były liczby, które odpowiadały ilości bydła rogatego jaką on posiadał oraz liczbie jeńców, których podobno przywiózł ze zwycięskich wypraw. Liczby te mówią, że Farmer posiadał 422 000 kóz, 400 000 bydła rogatego oraz 120 000 jeńców. Mogą być one zawyżone, alby wyolbrzymić jego wielkość i chwałę.
Podobny napis, do tego jaki został umieszczony na buławie widnieje na pomniku, który został wystawiony aby uczcić zwycięstwo egipskich wojsk nad nieprzyjacielem.
Jak już wiemy, system w jakim zapisywano liczby w Egipcie był oparty o podstawę 10. Aby oznaczyć jej kolejne potęgi, aż do siódmej, używano następujących znaków.
10.000.000 1.000.000 100.000 10.000 1.000 100 10 1
Sn HH Hfnw Dba xA St mDw Wa
Jedynka była graficznie oznaczana symbolem pałeczki czy tyczki, która służyła do mierzenia. Takimi kreskami oznaczano również liczby począwszy od jeden do dziewięciu.
Dziesięć oznaczano jako podkowę lub odwrócone U, co było symbolem pęta, którym krępowano krowy lub inaczej można wytłumaczyć ten symbol jako sznurek, którym wiązano kiedyś te pałeczki, aby były w wiązkach po 10. Tak więc w pisowni egipskiej można było do oznaczenia liczby 10 użyć symbolu, który kształtem przypominał odwrócone, duże U.
Sto było przedstawiane jako liść palmy, zwinięty, albo też zwiniętą linę, która służyła do odmierzania pól, czy spiralę lub jak sądzą niektórzy – laskę kapłańską.
Symbolem tysiąca był kwiat czy pęd lotosu, także symbol Nilu, dzięki któremu istniej Egipt. Dawniej też ten znak oznaczał „bardzo dużo”
Dziesięć tysięcy – jego symbolem był wskazujący palec, natomiast symbolem stu tysięcy – żaba, ponieważ uznano liczbę 100 000 za coś tak wielkiego, jak liczba żab po wylewie Nilu.
Liczba 1 000 000 była przedstawiona symbolem człowieka z rękami w górze, który był w stanie ekstazy. Prawdopodobnie tak przedstawiono boga, który podtrzymywał niebieskie sklepienie, jako symbol „wszystkiego” lub „nieskończoności”
Liczba 10 000 000 była oznaczana jako podkreślone koło lub słońce.
Gdy Egipcjanie zapisywali hieroglificznie liczby, obrazki odpowiadające jednościom, dziesiątkom, setkom i tak dalej, były pisane tyle razy ile ich było w danej liczbie, pisano je w odpowiednich rzędach, które były zapisywane w odwrotnej kolejności czyli od prawej do lewej.
Nie potrafimy dzisiaj jednoznacznie powiedzieć kiedy wymyślono ułamki, podobnie jak to mam miejsce z liczbami naturalnymi. Możemy jednak powiedzieć, że znak owalu, który dorysowywano do hieroglifów, o czym wspomniane było wcześniej, było początkiem ułamków. Jedno jest pewne, najwcześniej poznano ułamki, które odpowiadały połowie i ćwierci. Zostało to odkryte przez pewną europejską ekspedycję naukową koło połowy poprzedniego stulecia, na terenie Egiptu Górnego (dzisiaj Luxor). W starożytnych Tebach, które kiedyś były stolicą Egiptu, w ich ruinach, znaleziono papirus. Dzisiaj nazywa się do "papirusem Rhinda", Rhind to nazwisko angielskiego oficera, który go nabył w 1858r. na własność. Drukiem wydano go w tłumaczeniu w 1877 roku.
Na tym papirusie pisano tuszem czarnym i czerwonym (tak zwaną hieratyką, czyli pismem, które stosowano w codziennym życiu na papirusach. Uznano go za najstarszy matematyczny dokument świata.
Ahmes pisząc o "Sposobach do poznania wszelkich tajemnic" opisał wiele ciekawych informacji o egipskiej matematyce. Był to niejako materiał o usystematyzowanej formie matematycznego wykładu. Zadania w nim zawarte, były sklasyfikowane według tematów, a nie jak się robi to dzisiaj, według metod.
Najbardziej interesuje nas ta część dokumentu, w której opisano ułamki, znane w starożytnym Egipcie parę tysięcy lat temu.
Egipcjanie stosowali jedynie ułamki proste, ze tego względu, że łatwo je było zapisać. Ułamki proste to odwrotności liczb naturalnych. Pozostałe ułamki były przedstawiane za pomocą sumy różnych, prostych ułamków. Najtrudniejszy było dzielenie z resztą.
Egipcjanie zawsze zakładali, że licznik jest jedynką, zmienia się tylko mianownik. Ten sposób ułatwiał obliczenia, ale zapewniał również możliwość dokonywania obliczeń na niemalże wszystkich liczbach wymiernych, ponieważ liczba wymierna może być przedstawiona jako suma liczby całkowitej oraz skończone ilości ułamków prostych.
Najważniejsze zagadnienie dla Egipcjan dotyczyło dążenia do rozłożenie ułamków na sumę o różnych składnikach, gdzie składnikami są ułamki alikwotne mające liczniki równe jeden.
Tak więc Egipcjanie przedstawiali złożone ułamki za pomocą sumy ułamków o liczniku równym jeden.
Egipcjanie problem rozkładu ułamków na sumy ułamków alikwotnych rozwiązali empirycznie, ale w kilku etapach. Problem ten nie ma jednoznacznego rozwiązania. Ułożyli oni tablice kanoniczne, czyli w ustalonym porządku, dla rozkładów ułamków 2/n. Zaczęli od tych ułamków, ponieważ działaniem podstawowym przy dzieleniu jest podwajanie. Od tejże tablicy rozpoczyna się papirus Rhinda.
Dla rozkładów od n = 3 do n = 101 nie znamy drogi w jaki sposób je otrzymano. Aby rozwiązać tą zagadkę, pracowało nad nią wielu uczonych. Na podstawie wywodów B.L. Van der Waerdena musiano nauczyć się na pamięć najprostszych rozkładów, pojawiających się w każdym z kroków. W tekstach były one pisane bez dodatkowych wyjaśnień.
Były to ułamki proste, a działania wykonywane na nich były tak samo dobrze znane jak dzisiaj działania na całkowitych liczbach. Za ich pomocą można było wyprowadzić kilka innych zależności, z których niektóre podane zostały poniżej:
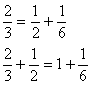
W Londynie znajduje się zwój, który pochodzi z około XVIII-XIX wieku p. n. e. W nim znajdują się zadania, które mówią o tym, że wyrażenia są dzielone przez 2, 3, 4 przez co otrzymuje się kolejną serię rozkładów.
Bardzo ważnym wzorem jest zależność obrazująca 2/3 jako ułamki egipskie. Od tego właśnie wzoru zaczęto tworzyć tablicę rozkładów kanonicznych przy pomocy podwajania ułamków. Ta część tablicy jest najstarszą częścią zwoju.
Zgłębiając ogólny przypadek rozkładu na proste ułamki okazało się, że należało podzielić tylko 2 przez n. Chociaż dzisiaj wydaje nam się to bardzo proste, to w tamtych czasach było to duże odkrycie. W taki właśnie sposób postępowali rachmistrzowie, którzy stworzyli tablice od n = 11.
Dzielenie przez następujące liczby: 5, 9, 11, 17, 23, 29 było wykonywane przy pomocy mnóstwa ułamków, które zaczynały się od 2/3, a 2/3 było ułamkiem tradycyjnym, naturalnym. Dzielenie kolei przez 7 i 13 było wykonywane przy pomocy ciągu rozpoczynającego się od 2.
Egipcjanie zapisywali ułamki takimi samymi znakami hieroglificznymi jak do zapisywania liczb naturalnych.
Jak już było napisane wyżej, aby odróżnić zwykłą liczbę od ułamka umieszczano obok lub nad symbolem mianownika hieroglif, który oznaczał to samo co dzisiaj znak odwrotności w potędze - „-1”. Dzielenie m przez n było czasami przedstawianie przez Egipcjan jako mnożenie m przez odwrotność liczby n.
Poza ułamkiem, który miał jedynkę w liczniku, starożytni stosowali ułamek 2/3, który był wyjątkiem. Miał on nawet swój własny symbol hieroglificzny.
Ułamki alikwotne są charakterystyczne dla początkowej fazy rozwoju liczb w cywilizacji starożytnej - ułamki typu 1/n były pierwszymi algorytmicznymi ułamkami.
W dalszych fazach rozwoju wymiernych liczb do użytku wprowadzono interpretację dla ułamka m/n – liczba całkowita mianowana. W starożytnym Egipcie matematyka nie rozwinęła się bardziej i nie wykroczyła poza ułamki podstawowe, które dzisiaj nazywamy egipskimi.
Poza wyżej przedstawionym zapisem w Egipcie operowano jeszcze innym systemem. Opierał się on na znaku oka, potężnym znaku boga–sokoła, Horusa, którego w mitologii pociął Set. Znak symbolizował życie oraz ochronę i był przedstawiany jako całość składająca się z 6 części. System oparty na „Oku Horusa” był systemem ułamkowym stosowanym przez Egipcjan przy mierzeniu gruntów, zboża oraz w receptach.
Na symbol składało się 6 elementów, które były wartościami ułamkowymi. Aby uzyskać ułamek należało dodać odpowiednie elementy z symbolu.
Aby zamienić dowolny ułamek na sumę prostych ułamków (dzisiaj nazywamy tą procedurę rozkładem) należało zastosować odpowiedni algorytm. Gdy oddzielono część całkowitą trzeba było odjąć największy z mniejszych prostych ułamków. Przy takiej operacji otrzymujemy ułamek - resztę, którego licznik maleje, a operacja jest skończona.
Egipcjanie mieli tablice dla rozkładów liczb 2/n, dla ułamka 2/3 był przyporządkowany osobny hieroglif.
Jeśli tak się określi ułamki, bardzo dużo pracy wymaga ich rozłożenie. Na papirusie Ahmesa można przeczytać następujące zadanie, które było postawione ówczesnym uczniom:
„Podzielić 100 bochenków chleba między 5 osób, w taki sposób, aby części im przydzielone utworzyły ciąg arytmetyczny, tak żeby 1/7 ilości bochenków jaką dostaną pierwsi trzej równała się licznie bochenków, którą otrzymają dwaj ostatni.”
Nawet dzisiaj, znając więcej metod, rozwiązanie tego zadania jest męczące. Tamci uczniowie musieli się bardzo natrudzić, aby je rozwiązać.
Starożytna matematyka była zespołem wiadomości, które nie były podzielone na geometrię, arytmetykę i algebrę. Składała się z przepisów na rozwiązanie liczbowe najprostszych z zadań arytmetycznych, geometrycznych czy algebraicznych. Egipcjanie mieli przeważnie problemy czysto praktyczne i większość rozwiązań było znajdowanych drogą prób i błędów.
Przyjmuje się, że geometria została odkryta w Egipcie, a zapoczątkowało ją mierzenie pól, natomiast rozwój ułamków ma korzenie w ułamkach egipskich.


