Trójkąt Pascala nie jest figurą geometryczną. Został on tak nazwany, ponieważ liczby, które w nim występują układają się w trójkąt. W wierzchołku trójkąta oraz wzdłuż boków wychodzących z tego wierzchołka są jedynki. Reszta liczb powstaje w ten sposób, że liczba będąca w kolejnym rzędzie jest sumą dwóch liczb, które są bezpośrednio nad nią. W poniższej tabeli zostały przedstawione początkowe liczby występujące w trójkącie Pascala.
|
Nr. wiersza
|
Trójkąt Pascala
|
Nr. wiersza
|
|
0.
1.
2.
3.
4.
5.
6.
7.
8.
...
|
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
......................................
|
0.
1.
2.
3.
4.
5.
6.
7.
8.
...
|
Nazwa Trójkąt Pascala jest ściśle związana z symbolem Newtona. Jeżeli przyjmiemy, że wiersze są numerowane od zera czyli, że w wierszu zerowym występuje tylko jedna liczba: jedynka, możemy obliczyć k - ty wyraz w n - tym wierszu:
k - ty wyraz w n - tym wierszu: 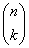
Przyjrzyjmy się teraz własnościom trójkąta Pascala. Jeśli umieścimy pierwsze 8 wierszy z Trójkąta Pascala w sześciokątach, każdy wyraz w osobnym, otrzymamy:
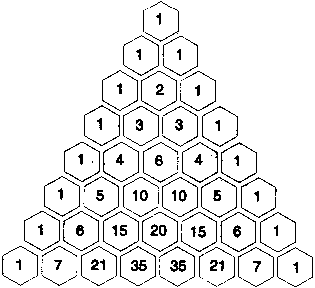
Zakreślmy teraz wszystkie sześciokąty, w których występują liczby nieparzyste, natomiast te z liczbami parzystymi zostawmy puste. Dostaniemy następujący trójkąt:
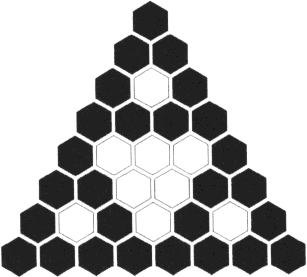
Widoczna jest tutaj pewna zależność. Przyjrzyjmy się temu na większej ilości wierszy. Jeżeli weźmiemy początkowe 64 wiersze i postąpimy z nimi podobnie jak poprzednio, czyli umieścimy w sześciokątach i zamalujemy liczby nieparzyste, otrzymamy:

Tutaj również widać pewną zależność. Poprzez takie oto zamalowywanie liczb nieparzystych otrzymujemy z Trójkąta Pascala rysunki, które coraz lepiej przypominają Trójkąt Sierpińskiego.


