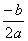Trójmianem kwadratowym nazywamy równanie postaci: ax2 + bc + c = 0, gdzie a ≠ 0. Aby rozwiązać takie równanie najwygodniej skorzystać z tak zwanej postaci kanonicznej. Aby w ten sposób przedstawić trójmian kwadratowy należy wyliczyć wyróżnik trójmianu kwadratowego (
). Deltę wyliczamy ze wzoru: ∆ = b2 - 4ac
Gdy już mamy wyliczony wyróżnik, należy rozpatrzyć trzy przypadki.
Przypadek 1:
Jeżeli jest mniejsza od zera, równanie nie ma rozwiązania.
Przypadek 2:
Jeżeli ∆ > 0równanie ma dwa rozwiązania: x1 =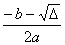 
, x2 =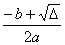 
Przypadek 3:
Jeżeli ∆ = 0 równanie ma jedno podwójne rozwiązanie: x0 = 
