Przy jakich wartościach parametru m równanie x2 - (m - 5) x + m2 - 6m + 5 = 0
ma 2 pierwiastki o różnych znakach?
1) 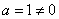
2) 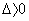
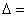 [-(m -5)]2 -
[-(m -5)]2 - 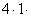 ( m2 - 6m + 5) = m2 - 10m + 25 - 4m2 + 24m - 20 = - 3m 2 + 14m +5
( m2 - 6m + 5) = m2 - 10m + 25 - 4m2 + 24m - 20 = - 3m 2 + 14m +5
- 3m 2 + 14m +5 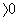
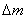 = 142 - 4
= 142 - 4 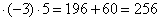
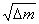 = 16
= 16
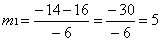 lub
lub 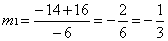
 |

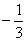 5
5
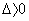
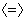
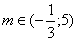
3) 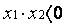
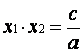
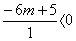
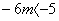
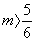

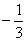 0
0 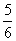 5
5
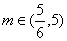
Odp. Równanie ma 2 pierwiastki o różnych znakach dla 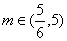 .
.
Zadanie 2.
Rozwiąż równanie:
| x + 5 | + | x - 6 | = 9 - x
|
| ||
|
- 5
|
0 1 6
| |
1) załóżmy, gdy 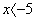 to | x + 5| = - ( x + 5 ) i | x - 6 | = - (x - 6)
to | x + 5| = - ( x + 5 ) i | x - 6 | = - (x - 6)
- ( x + 5 ) - ( x - 6 ) = 9 - x
- x - 5 - x + 6 = 9 - x
- x - x + x = 9 + 5 - 6
- x = 8
x = - 8
2) załóżmy, gdy c- 5 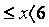 to | x + 5| = x + 5 i | x - 6 |
to | x + 5| = x + 5 i | x - 6 |
x + 5 - ( x - 6 ) = 9 - x
x + 5 - x + 6 = 9 - x
x = 9 - 5 - 6
x = - 2
3) załóżmy, gdy 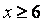 to | x + 5 | = x + 5 i | x - 6 | = x - 6
to | x + 5 | = x + 5 i | x - 6 | = x - 6
x + 5 + x - 6 = 9 -x
3x = 9 - x
3x = 10
x = 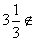 zbioru rozwiązań
zbioru rozwiązań
Odp. Rozwiązaniem równania są: x = - 8 lub x = - 2
Zadanie 3.
Rozwiąż równanie:
tg x + ctg x = 4 sin 2x
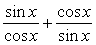 = 4 sin 2x
= 4 sin 2x
sin2 x + cos2x
 cos x sin x = 4 sin 2x
cos x sin x = 4 sin 2x
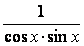 = 4 sin 2x
= 4 sin 2x
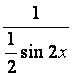 = 4 sin 2x
= 4 sin 2x
2 sin2 2x = 1
sin2 2x = 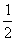
sin 2x = 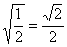 lub sin 2x = -
lub sin 2x = - 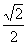
 |

xo =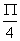 0 X
0 X
Odp. 2 x1 = 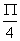 + 2 k
+ 2 k 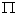 lub 2x2 =
lub 2x2 = 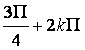 lub 2x3 =
lub 2x3 = 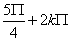
lub 2x4 = 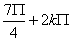
x1 = 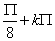 lub x2 =
lub x2 = 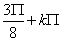 lub x3 =
lub x3 = 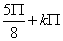 lub x4 =
lub x4 = 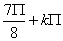
dla 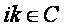
Zadanie 4.
Liczby a, b, c, to kolejne wyrazy ciągu arytmetycznego, natomiast liczby b, c, d to kolejne wyrazy ciągu geometrycznego. Sumując pierwszą trójkę otrzymamy 12, drugą 19. Wyznaczyć wartości liczb a, b, c, d.
a + b + c = 12 i b + c +d = 19 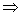 ( b + c + d) - ( a + b + c) = d - a = 7
( b + c + d) - ( a + b + c) = d - a = 7
d = a + 7
a, b = a + r, c = a + 2r, d = a + 7
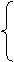 a + a + r + a + 2r = 12
a + a + r + a + 2r = 12
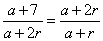
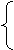
3a + 3r = 12
a2 + ar + 7a + 7r = a2 + 4ar + 4r2
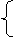 a + r = 4
a + r = 4
- 3ar - 4r2 + 7a + 7r = 0
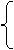
a = 4 - r
- 3 ( 4 - r ) r - 4r2 + 7 (4 - r) + 7r = 0
-12r + 3 r2 - 4r2 + 28 - 7r + 7r = 0
- r2 - 12r + 28 = 0
r2 + 12r - 28 = 0
 = 122 -
= 122 - 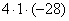 = 144 + 122 = 256,
= 144 + 122 = 256, 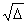 =16
=16
r1 = 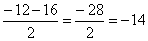 lub r2 =
lub r2 = 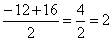
 a1 = 4 - ( - 14) a2 = 4 - 2
a1 = 4 - ( - 14) a2 = 4 - 2
r1 = - 14 r2 = 2
 |  |
a1 = 18 a2 = 2
r1 = 14 r2 = 2
18, 4, -10, 25 2, 4, 6, 9
Odp. Liczby a, b, c, d wynoszą odpowiednio: 18, 4, -10, 25 albo 2, 4, 6, 9 .



