Kombinatoryka
Kombinatoryka jest teorią obliczania licznych elementów skończonych zbiorów. Powstała przez gry hazardowe, a rozwinęła się dzięki rachunkowi prawdopodobieństwa, teorii informacji, teorii grafów i innym częściom matematyki stosowanej. kombinatoryk jest pozornie odrębną nauką, ponieważ posługuje się specyficzną terminologią. Uczniowie zaczynają się jej uczyć w szkole ze względu na zastosowanie w rachunku prawdopodobieństwa. Kombinatoryka zajmuje się głównie konstrukcją odwzorowań idących z jednego zbioru skończonego do drugiego, ale muszą być spełnione pewne określone warunki oraz znajdowaniem wzorów na ilość tych odwzorowań.
Permutacja
Permutacja jest odwzorowaniem różnowartościowym skończonego zbioru w siebie.
Liczba 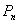 permutowań w zbiorze
permutowań w zbiorze  -elementowym dana jest wzorem:
-elementowym dana jest wzorem:
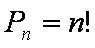
Trzeba odróżnić permutacje wykonywane na zbiorze od permutacji zbioru.
Permutowaniem  -elementowego zbioru
-elementowego zbioru 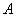 lub inaczej ustalaniem porządku elementów występujących w tym zbiorze jest każde odwzorowanie różnowartościowe z
lub inaczej ustalaniem porządku elementów występujących w tym zbiorze jest każde odwzorowanie różnowartościowe z 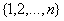 do
do 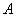 .
.
Oba te pojęcia pokrywają się, gdy 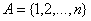 .
.
Kombinacja
Kombinacją nazywamy każdy podzbiór skończonego zbioru.
Kombinacją po
po 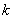 jest każdy
jest każdy 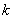 -elementowy podzbiór zbioru
-elementowy podzbiór zbioru  -elementowego (
-elementowego (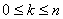 ).
).
Dopełnieniem kombinacji  po
po 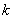 jest kombinacja
jest kombinacja  po
po 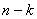 .
.
Liczba permutacji na kombinacji z  po
po 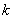 równa jest
równa jest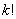
Liczba permutacji na kombinacji dopełniającej równa jest 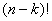
Więc każdej kombinacji  po
po 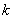 odpowiada
odpowiada 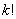
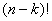 permutacji w zbiorze
permutacji w zbiorze  -elementowym.
-elementowym.
Jeśli przez 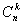 oznaczymy liczbę wszystkich kombinacji
oznaczymy liczbę wszystkich kombinacji  po
po 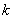 ,
,
to 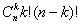 -- liczba wszystkich permutacji w zbiorze
-- liczba wszystkich permutacji w zbiorze  -elementowym, mamy:
-elementowym, mamy:
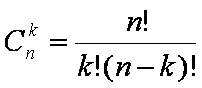
Symbol 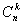 jest zastępowany najczęściej przez symbol Newtona
jest zastępowany najczęściej przez symbol Newtona 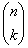 .
.
Wariacja
Wariacją jest odwzorowanie różnowartościowe podzbioru zbioru skończonego w niego samego.
Wariacja  po
po 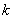 jest odwzorowaniem różnowartościowym
jest odwzorowaniem różnowartościowym 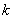 -elementowego podzbioru zbioru
-elementowego podzbioru zbioru  -elementowego
-elementowego 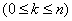 w niego samego.
w niego samego.
Liczba 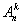 wszystkich wariacji
wszystkich wariacji  po
po 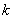 równa się liczbie wszystkich odwzorowań różnowartościowych zbioru
równa się liczbie wszystkich odwzorowań różnowartościowych zbioru 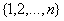 w dowolny
w dowolny  -elementowy zbiór
-elementowy zbiór 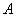 , tzn. równy liczbie permutacji we wszystkich
, tzn. równy liczbie permutacji we wszystkich 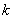 -elementowych podzbiorach zbioru
-elementowych podzbiorach zbioru 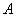 , czyli we wszystkich kombinacjach
, czyli we wszystkich kombinacjach  po
po 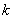 , mamy:
, mamy:
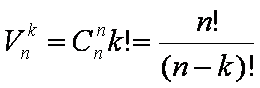
Przykład:
Z cyfr 1,2,3,4 możemy utworzyć 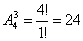 liczb trzycyfrowych o różnych cyfrach.
liczb trzycyfrowych o różnych cyfrach.
Wariacja z powtórzeniami
Wariacja z powtórzeniami jest każdym odwzorowaniem podzbioru zbioru skończonego w niego samego.
Wariacją z powtórzeniami  po
po 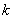 jest każde odwzorowanie podzbioru
jest każde odwzorowanie podzbioru 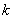 -elementowego zbioru
-elementowego zbioru  -elementowego w niego samego. Liczba wszystkich wariacji z powtórzeniami
-elementowego w niego samego. Liczba wszystkich wariacji z powtórzeniami  po
po 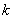 wynosi
wynosi 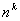 .
.
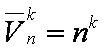
Przykład:
Za pomocą cyfr 1,2,3,4 możemy napisać 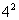 liczb dwucyfrowych (niekoniecznie muszą być one o różnych cyfrach).
liczb dwucyfrowych (niekoniecznie muszą być one o różnych cyfrach).
Silnia
Funkcję 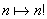 , określamy w sposób następujący w zbiorze liczb naturalnych:
, określamy w sposób następujący w zbiorze liczb naturalnych: 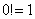 ,
, 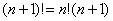 .
.
Z powyższego określenia otrzymujemy 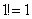 ,
,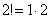 ,
, 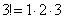
Ogólnie 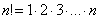 dla
dla 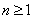 .
.
Wartości 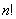 rosną szybko, np.
rosną szybko, np. 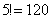 ,
, 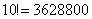 ,
, 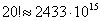 .
.
Oby obliczyć przybliżoną wartość 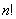 korzystamy ze wzoru Stirlinga:
korzystamy ze wzoru Stirlinga: 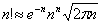 .
.
Symbol Newtona
Symbolem Newtona jest funkcja 2 zmiennych, określona następującymi wzorami (gdzie n rzeczywiste i k naturalne).
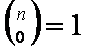 ,
,
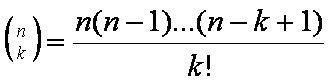
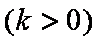
Jeżeli  naturalne to symbol Newtona jest równy
naturalne to symbol Newtona jest równy 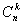 , tzn. jest to liczba kombinacji
, tzn. jest to liczba kombinacji  po
po 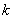 .
.
Pierwszy raz symbol Newtona wykorzystano przy rozwinięciu funkcji 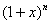 w tzw. szereg potęgowy Newtona:
w tzw. szereg potęgowy Newtona: 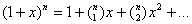 , jest on zbieżny dla
, jest on zbieżny dla 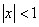 .
.
Na przykład 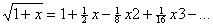
W związku z tym, że dla  naturalnych oraz dla
naturalnych oraz dla 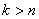 symbol Newtona równy jest
symbol Newtona równy jest 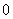 , stąd dla
, stąd dla 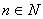 szereg potęgowy Newtona upraszcza się do tak zwanego dwumianowego wzoru Newtona:
szereg potęgowy Newtona upraszcza się do tak zwanego dwumianowego wzoru Newtona: 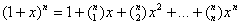 .
.
W szczególnym przypadku, dla 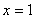 otrzymamy
otrzymamy 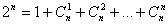 , tzn. jest to liczba wszystkich podzbiorów zbioru
, tzn. jest to liczba wszystkich podzbiorów zbioru  -elementowego (razem ze zbiorem pustym i całym zbiorem) równa jest
-elementowego (razem ze zbiorem pustym i całym zbiorem) równa jest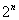 .
.
Ponieważ 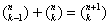 i
i 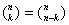 , dla k i n naturalnych oraz takich, że
, dla k i n naturalnych oraz takich, że 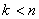 oraz
oraz 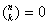 dla
dla  naturalnego oraz
naturalnego oraz 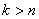 .
.
Stąd symbole Newtona tworzą łatwo konstruowalną tablicę trójkątną, nazywaną inaczej trójkątem Pascala:
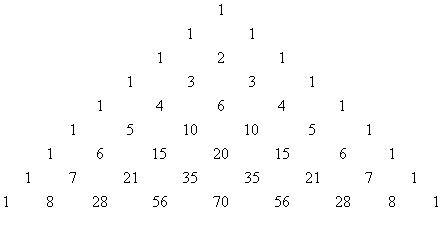
Każdy kolejny wiersz powstaje w ten sposób, że na brzegach są jedynki, a w środku liczby powstają jako suma dwóch wyrazów występujących bezpośrednio nad nim.


