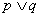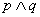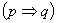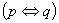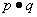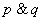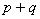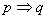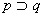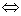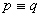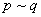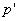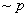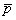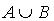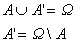Logika matematyczna - elementy

Zdaniem w sensie matematycznym to zdanie, o którym można powiedzieć jednoznacznie, że jest prawdziwe lub fałszywe.

Wartością logiczną dla zdania prawdziwego jest 1, natomiast dla zdania fałszywego wartością logiczną jest 0.

Zdania najczęściej oznacza się przez litery: p, q, r i tak dalej.

Funkcją zdaniową (formą zdaniową) jest wyrażenie, stające się zdaniem logicznym po wstawieniu na miejsce zmiennej x każdego z elementów należących do dziedziny.

Negacją (zaprzeczeniem) zdania p jest zdanie „nieprawda, że p” oznaczamy go przez:  ~p

p	~ p
1 0	0 1

Koniunkcją zdań p i q jest zdanie „p i q”, co oznaczamy: p 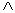 q

Alternatywą zdań p i q jest zdanie „p lub q”, co oznaczamy p 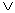 q

p	q
1 1 0 0	1 0 1 0	1 1 1 0	1 0 0 0

Implikacją (wynikaniem) zdań p i q jest zdanie „jeżeli p, to q”, co oznaczamy: p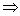 q

Równoważnością zdań p i q jest zdanie „p wtedy i tylko wtedy, gdy q”, co oznaczamy: p 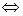q

p	q
1 1 0 0	1 0 1 0	1 1 1 0	1 0 0 0

PRAWA DOTYCZĄCE RACHUNKU ZDAŃ

Zdanie logiczne możemy nazwać tautologią, jeżeli jest prawdziwe zawsze, niezależnie jakie będą wartości zmiennych logicznych, jakie w nim występują.

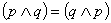prawo przemienności koniunkcji

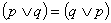prawo przemienności alternatywy

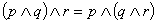  prawo łączności koniunkcji

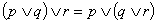  prawo łączności alternatywy

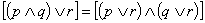  prawo rozdzielczości alternatywy

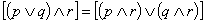  prawo rozdzielczości koniunkcji

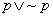  prawo wyłącznego środka

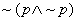  prawo sprzeczności

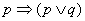    prawo pochłaniania

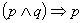  prawo pochłaniania

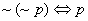prawo podwójnego zaprzeczenia

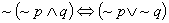zaprzeczenie koniunkcji - ekskluzja

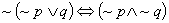zaprzeczenie alternatywy - binegacja

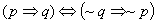  prawo transpozycji

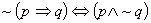prawo zaprzeczenia implikacji

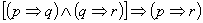  prawo przechodniości implikacji

KWANTYFIKATORY

Kwantyfikator ogólny

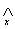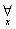 lub  oznacza: „dla każdego x należącego do….”

Kwantyfikator szczegółowy

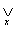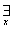 lub  oznacza: „istnieje takie x należące do…”

Prawa de'Morgana dla kwantyfikatorów:

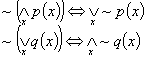
SYMBOLIKA

nazwa	symbol	język	symbolika
			Schrödera-Pierce’a	Peano-Russella	Hilberta	Łukasiewicza
koniunkcja		p i q				Kpq
alternatywa		p lub q				Apq
implikacja		jeżeli p, to q				Cpq
równoważność		p wtedy i tylko wtedy, gdy q				Epq
negacja	~	nie p				Np

DZIAŁANIA NA ZBIORACH

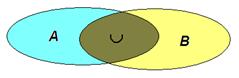
Suma zbiorów

Suma zbiorów A i B  to zbiór elementów, które należą do zbioru A lub należą do zbioru B. Sumę zbiorów oznacza się symbolem

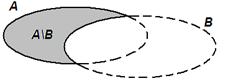
Różnica zbiorów

Różnica zbiorów A i B to zbiór składający się z elementów, które należą do zbioru A ale nie należą do zbioru B. Różnicę zbiorów oznacza się symbolem AB

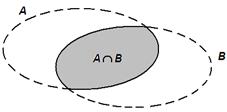
Iloczyn zbiorów

Iloczyn (część wspólna) zbiorów A i B to zbiór elementów, które należą jednocześnie do zbioru A oraz do zbioru B. Iloczyn zbiorów oznacza się symbolem

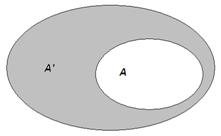
Dopełnienie zbioru do przestrzeni

Ω- ustalony zbiór A podzbiór właściwy zbioru Ω Różnica zbiorów Ω i A jest dopełnieniem zbioru A względem zbioru Ω. Dopełnienie zbioru A oznaczamy symbolem A'.