Spis treści:
Isaac Newton – wybitny uczony
Nazwisko wybitnego fizyka, matematyka i astronoma zna nawet uczeń szkoły podstawowej. Isaac Newton żył na przełomie XVII i XVIII wieku. Poświęcał też sporo czasu na prace alchemiczne i studia teologiczne. Był pierwszym uczonym, który został uhonorowany szlachectwem.
Isaac Newton jest znany z tego, że odkrył prawo powszechnego ciążenia, jako pierwszy opisał trzy zasady dynamiki, skonstruował teleskop zwierciadlany. W publikacji „New Theory about Light and Colors” („Nowa teoria światła i barw”) napisał, że światło białe jest mieszaniną różnych barw, a każda z nich ma ściśle określony współczynnik załamania.
Miał wiele innych osiągnięć, ale bał się publikować wyników swoich prac od razu. Współcześni znali matematyczne odkrycia Newtona z listów lub rękopisów. Podobno był rozdarty między chęcią sławy a obawą przed krytyką.
Przeczytaj również: Zagadka Libuszy. Jak czeska księżniczka potraktowała zalotników?
Zagadka Newtona
Nie musisz być wybitnym naukowcem ani znać realiów, w jakich żył Isaac Newton, aby rozwiązać zagadkę Newtona. Przeczytaj uważnie treść.
Na łące rośnie trawa. Aż sześćdziesiąt krów mogłoby paść się na tej łące przez czternaście dni. A pięćdziesiąt krów mogłoby paść się przez dwadzieścia osiem dni. Ile krów mogłoby paść się stale na tej łące dzięki stale i równomiernie odrastającej trawie?
Tego zadania nie rozwiążesz raczej w pamięci, więc przygotuj kartkę i długopis. Nie sprawdzaj od razu odpowiedzi. Spróbuj samodzielnie rozwikłać matematyczną łamigłówkę. Zaczynamy?
Przeczytaj również: Łamigłówka matematyczna. Wyliczysz w pamięci w 10 sekund?
Rozwiązanie zagadki
Jeżeli nie udało ci się znaleźć poprawnej odpowiedzi, to sprawdź wersję rozwiązania, którą podał podobno sam Isaac Newton.
Najpierw wypisz wszystkie niewiadome. Załóżmy, że:
- t – oznacza początkową ilość trawy, która rośnie na łące
- x – oznacza ilość trawy, która odrasta w ciągu jednego dnia
- y – oznacza ilość trawy, którą jednego dnia zjada krowa
Informacje zawarte w łamigłówce pozwalają na stworzenie układu równań:
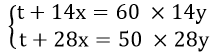
Teraz należy odjąć stronami pierwsze równanie od drugiego:
14x = 1400y – 840y
14x = 560y
x = 40y
Aby dowiedzieć się, ile krów mogłoby się paść na stałe na łące, wystarczy podstawić wyznaczone wyrażenie do pierwszego równania układu.
t + 14 × 40y = 60 × 14y
t + 560y = 840y
t = 280y
t = 7 × 40y = 7x
x = 40y
Jeżeli założymy, że trawa rośnie na łące równomiernie, to na stałe może się tam paść 40 krów.
Źródła: encyklopedia.pwn.pl, starchild.gsfc.nasa.gov, zpe.gov.pl
Redakcja
Rozwiąż inne zagadki:
Zagadka słowna dla sprytnych. Podejmiesz wyzwanie?
Rebus Tuwima. Kto by pomyślał, że rozwiązanie jest aż tak proste
Zagadki z „Lalki” Bolesława Prusa. Wystarczy chwilę pomyśleć


