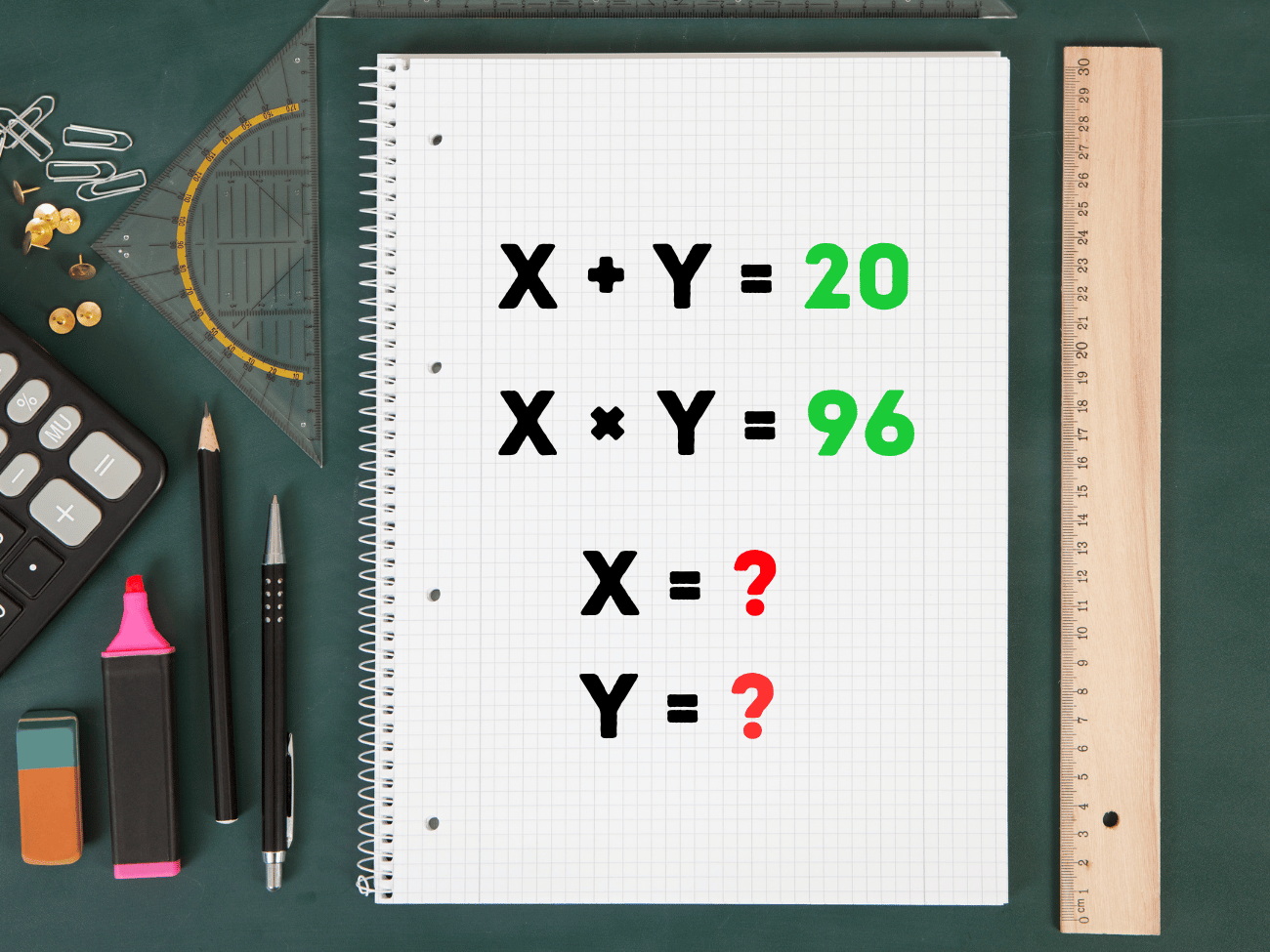Zagadka na opak. Jakie liczby mnożą się do 96 i sumują do 20?

W zagadkach matematycznych zwykle chodzi o rozwiązanie prowadzące do prawidłowego wyniku. Tym razem zadanie będzie dokładnie odwrotne – znając wynik musimy "odszukać" składowe równania. Wiesz, jak to zrobić? Jeśli tak, to z matematyką radzisz sobie lepiej niż 95 proc. społeczeństwa!

Spis treści:

Tajemnicze liczby. Odwrócona zagadka matematyczna
Jak rozwiązać zagadkę? Podpowiedź
Rozwiązanie odwróconej zagadki. Krok po kroku
Delta w praktyce. Nie tylko do męczenia uczniów

Tajemnicze liczby. Odwrócona zagadka matematyczna

Dwie liczby sumują się do 20. Kiedy mnożysz je przez siebie, otrzymujesz 96. Jakie to liczby?

Z pozoru brzmi to jak proste równanie, ale czy na pewno? Zastanów się przez chwilę – to zadanie wymaga zarówno intuicji, jak i sporych umiejętności w operowaniu liczbami.

Jak rozwiązać zagadkę? Podpowiedź

Pierwszym krokiem w tego typu zagadkach jest sformułowanie dwóch równań. Mając dwie liczby – x oraz y – wiesz, że:

suma: x + y = 20

iloczyn: x × y = 96

Masz zatem dwa kluczowe równania, które prowadzą do rozwiązania. Jaką ścieżkę obrać, żeby dotrzeć do wartości iksa i igreka? To ta, nad którą widnieje duży trójkąt – delta.

W kolejnej części artykułu znajdziesz działania, które prowadzą do prawidłowego rozwiązania, dlatego – jeśli chcesz zrobić to samodzielnie – wstrzymaj się z dalszą lekturą.

Rozwiązanie odwróconej zagadki. Krok po kroku

Z równania x+y = 20 można wyprowadzić jedną zmienną w zależności od drugiej. Załóżmy, że wyznaczasz y, wtedy y = 20 - x. Po podstawieniu tej zależność do drugiego równania (iloczynu) i krótkich obliczeniach otrzymujemy klasyczne równanie kwadratowe. Wszyscy licealiści już wiedzą, co to oznacza...

Nie unikniemy wyliczania delty i miejsc zerowych.

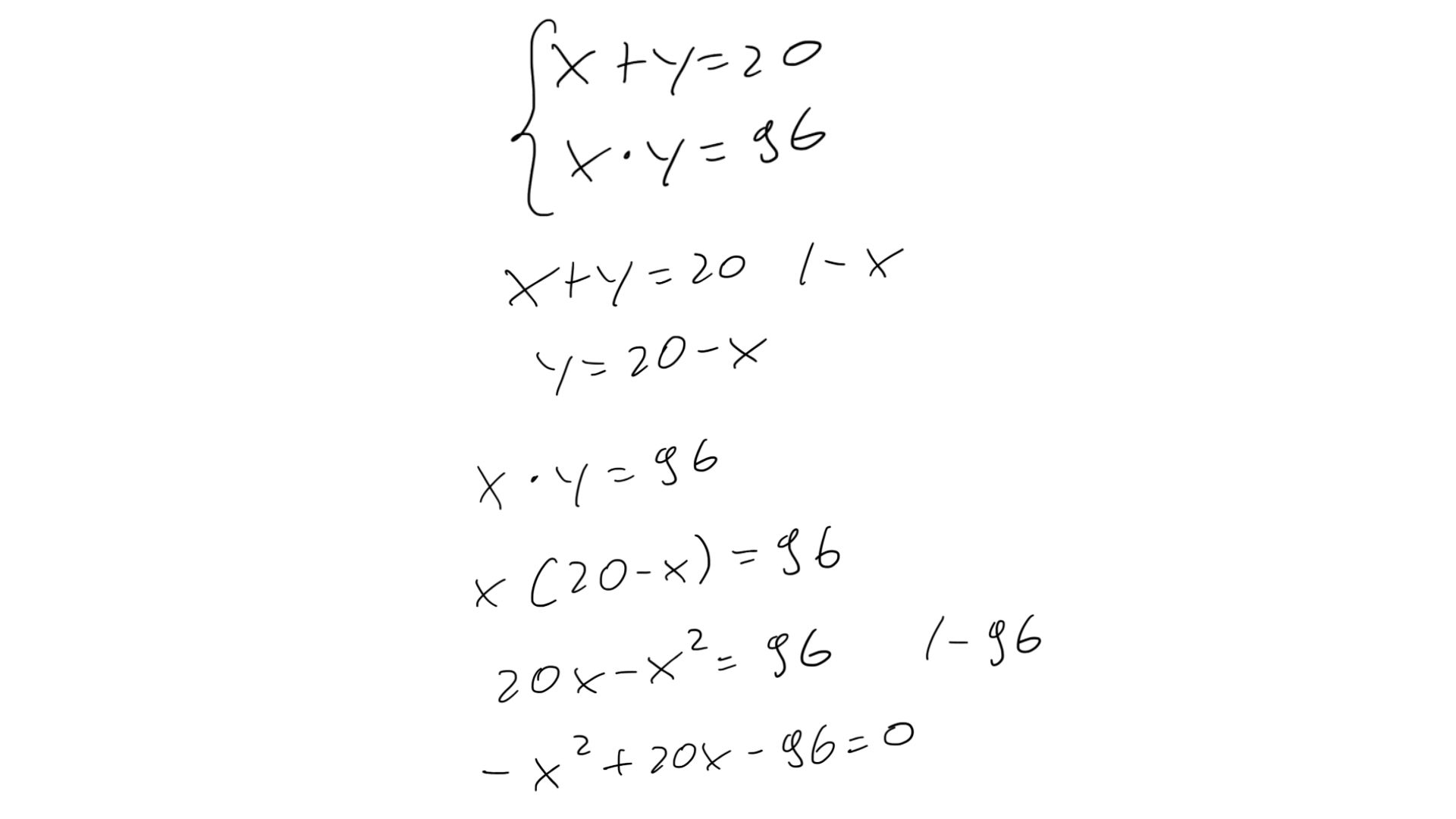
rozwiazanie zagadki z delta czesc 1 — Kiedy znamy wyniki i szukamy składowych równań, które je tworzą musimy jakoś pozbyć się jednej niewiadomej. Kiedy ograniczymy ich liczbę do 1 pojawią się nowe możliwości, które pozwolą ustalić obie szukane wartości /rys. bryk.pl

Czas rozwiązać równanie kwadratowe. To oznacza, że w następnych krokach skorzystamy z 3 wzorów: jednego, który pozwoli obliczyć deltę i dwóch do określania miejsc zerowych. Dwie wartości będą jednocześnie rozwiązaniem naszej zagadki. Jak to zrobić? Wszystko wyjaśniają poniższe obliczenia:

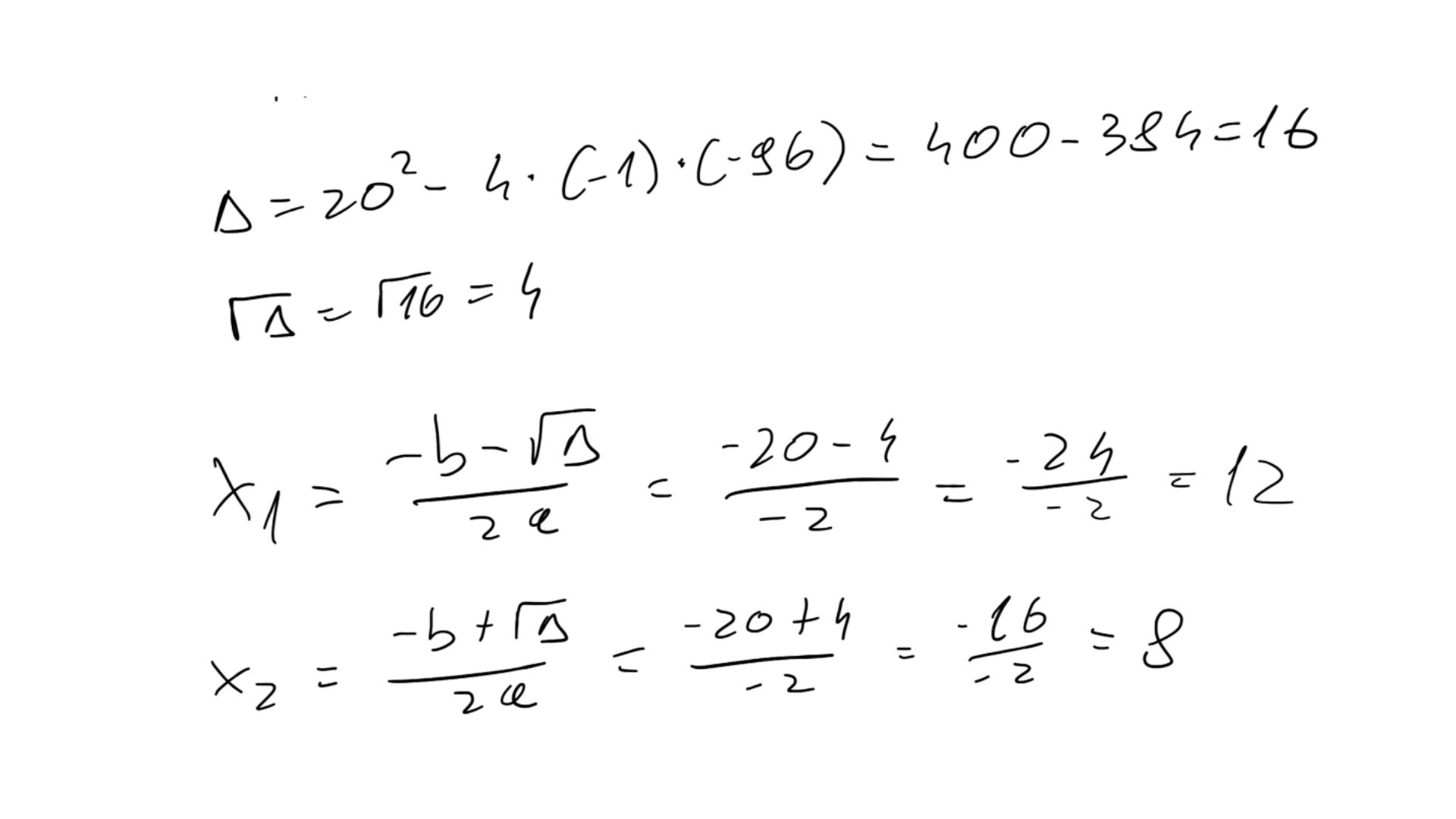
rozwiazanie zagadki z delta czesc 2 — /rys. bryk.pl

Tajemnicze liczby to 12 i 8! Te dwie liczby sumują się do 20, a ich iloczyn wynosi 96.

Delta w praktyce. Nie tylko do męczenia uczniów

Rozwiązywanie równań kwadratowych, takich jak to, którym zajmowaliśmy się powyżej, jest nie tylko matematyczną "sztuką dla sztuki" – przeciwnie, znajduje szerokie zastosowanie w wielu dziedzinach. Wzór na deltę, czyli inaczej wyróżnik równania kwadratowego, jest wykorzystywany np. w fizyce, gdzie służy do opisu ruchu ciał, obliczania prędkości i przyspieszenia. W ekonomii równania kwadratowe pozwalają przewidywać zyski i ryzyko inwestycyjne (przynajmniej tak twierdzą inwestorzy, którzy ich używają).

Z kolei inżynierowie często korzystają z takich obliczeń podczas projektowania konstrukcji, aby przewidywać zachowanie materiałów pod wpływem różnych sił (np. w różnych warunkach atmosferycznych). Jak widać matematyka, której uczymy się w szkole, jest podstawowym narzędziem w codziennym życiu wielu specjalistów.