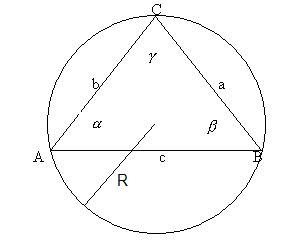
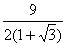Mamy dany trójkąt ABC o bokach długości: a, b, c oraz miarach kątów wewnętrznych 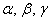. Niech R oznacza promień okręgu, który jest opisany na trójkącie ABC. Przedstawia to poniższy rysunek:

Twierdzenie sinusów:

W dowolny trójkącie stosunek długości boku trójkąta do sinusa kąta leżącego naprzeciwko jest dla danego trójkąta stały i równy średnicy okręgu opisanego na tym trójkącie.

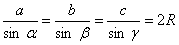
Twierdzenie cosinusów(Carnota):

W dowolnym trójkącie kwadrat długości jednego boku równy jest sumie kwadratów długości dwóch pozostałych boków pomniejszony o podwojony iloczyn długości tych boków i cosinus kąta zawartego między tymi bokami.

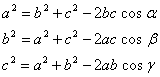
Gdy znamy długości dwóch boków trójkąta oraz miarę kąta zawartego pomiędzy nimi, to pole trójkąta możemy obliczyć z poniższego wzoru:

P = 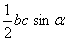lub

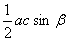P = lub

P=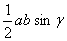

Przykład:

Mamy dany trójkąt o długości boku c = 3cm oraz kątach 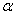= 450 oraz

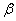= 300. Obliczyć pole trójkąta.

Rozwiązanie:

Skorzystamy ze wzoru P= 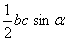, do tego potrzebna nam jest długość boku b. Obliczymy go z twierdzenia sinusów.

 

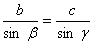
Miarę kąta 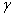 obliczymy na podstawie wiadomości, że suma kątów w trójkącie równa jest 1800:

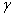= 1800 -  -

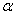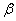
sin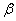 = sin 300 =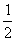

sin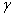 = sin (1800 - (450 + 300)) = sin (450 + 300) =

= sin 300 cos 450 + sin 450 cos 300 = =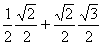 

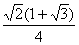
Obliczamy b:

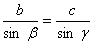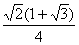 =>b () = 3 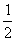 => b =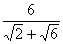

Stąd pole trójkąta wynosi:

P = 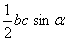 = 3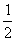 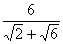sin 450 =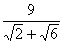 =
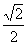