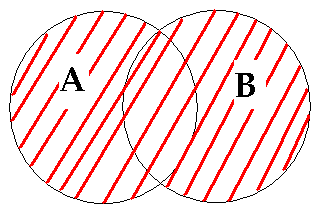
Sumą pewnych zbiorów A i B nazywamy taki zbiór, do którego należą te i tylko te elementy, które należą do co najmniej jednego ze zbirów A i B. sumę zbiorów A i B oznaczamy przez A 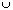 B.
B.
Określenie to możemy również zapisać za pomocą wzoru:
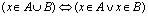
Sumę zbiorów A i B przedstawia zakreskowana na rysunku 1 część figury.

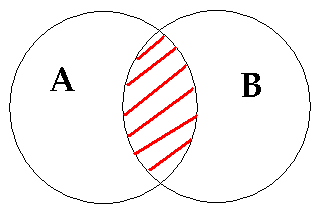
Iloczynem (inaczej częścią wspólną) pewnych zbiorów A i B nazywamy taki zbiór, do którego należą te i tylko te elementy, które należą do obu zbiorów A i B. iloczyn zbiorów A i B oznaczamy przez A 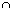 B.
B.
Określenie to możemy również zapisać za pomocą wzoru:
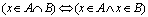
Sumę zbiorów A i B przedstawia zakreskowana na rysunku 2 część figury.

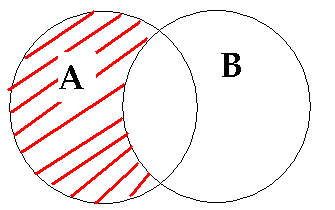
Różnicą pewnych zbiorów A i B nazywamy taki zbiór, do którego należą te i tylko te, które należą do zbioru A i nie należą do zbioru B. Różnicę zbiorów oznaczamy przez A-B lub A/B.
Określenie to możemy również zapisać za pomocą wzoru:
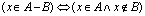
Sumę zbiorów A i B przedstawia zakreskowana na rysunku 3 część figury.
Natomiast zbiorami rozłącznymi nazywamy takie zbiory A i B, które nie mają wspólnych elementów. Inaczej mówiąc, dwa zbiory są rozłączne, jeśli ich część wspólna jest zbiorem pustym, tzn. 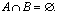
ĆWICZENIA
- Znajdź sumę zbiorów A i B, gdzie:
a). A={0, 1, 2}, B={1, 2, 3}
b). A={4, 6, 13, 567}, B= 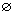
c). A={x: 1
a). A={1, 2, 3}, B={1, 2, 4}
b). A={1, 6, 7, 14}, B= 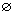
c). A={x: -1
a). A={1, 2, 3}, B={1, 2, 3}
b). A={1, 2, 3}, B={1, 3, 4}
c). A={1, 2, 3}, B={6, 7, 8}
- Znajdź zbiór
![00029056.png]() oraz zbiór
oraz zbiór ![00029057.png]() i porównaj wyniki, mając dane:
i porównaj wyniki, mając dane:
a). A={1, 2, 3, 4, 5, 6, 7}, B={1, 3}, C={1, 7}
b). A={x: 1 c). A={x: x a). b). 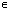 R}, B={x: 2
R}, B={x: 2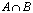 i
i 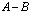
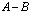 i
i 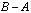
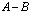 jest zbiorem pustym, to czy A=B?
jest zbiorem pustym, to czy A=B?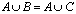 , to czy B=C?
, to czy B=C?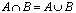 , to czy A=B?
, to czy A=B?

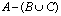 oraz zbiór
oraz zbiór 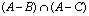 i porównaj wyniki, mając dane:
i porównaj wyniki, mając dane:
