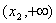I. Ogólny schemat
Aby powiedzieć coś na temat przebiegu zmienności funkcji, którą mamy podaną wzorem jawnym należy sprawdzić jej kilka własności, dzięki którym będzie można powiedzieć więcej na temat jej przebiegu, czyli o kształcie jej wykresu.
Badanie przebiegu zmienności funkcji sprowadza się do postępowania według pewnego schematu, który przedstawić jest najwygodniej w punktach, według kolejności postępowania:
1. Analiza funkcji, czyli własności wynikające bezpośrednio z jej wzoru.
- wyznaczenie dziedziny funkcji
- zbadanie parzystości, nieparzystości, okresowości, itd.
- wyznaczenie punktów nieciągłości funkcji
- wyznaczenie granic funkcji na krańcach przedziałów jej określoności
- wyznaczenie asymptot
- wyznaczenie punktów przecięcia wykresu funkcji z obiema osiami układu współrzędnych
- Analiza pierwszej pochodnej, czyli zbadanie własności funkcji, które wynikają z własności pierwszej pochodnej.
- obliczenie pierwszej pochodnej
- wyznaczenie dziedziny pierwszej pochodnej i punktów jej nieciągłości
- wyznaczenie przedziałów monotoniczności funkcji, czyli przedziałów w których pierwsza pochodna jest dodatnia, ujemna lub równa się zero
- wyznaczenie ekstremów funkcji
- w punktach, gdzie funkcja jest różniczkowalna
- w punktach, gdzie funkcja nie jest różniczkowalna
- Analiza drugiej pochodnej, czyli zbadanie, czyli zbadanie własności funkcji, które wynikają z własności drugiej pochodnej.
- obliczenie drugiej pochodnej
- wyznaczenie dziedziny drugiej pochodnej i punktów jej nieciągłości
- wyznaczenie przedziałów, w których funkcja jest wklęsła i wypukła, czyli przedziałów, gdzie druga pochodna jest dodatnia, ujemna lub równa się zero
- wyznaczenie punktów przegięci funkcji
- Sporządzenie zestawienia tabelarycznego wszystkich wyników
- Sporządzenie wykresu funkcji
Powyższy schemat nie jest szablonem, według którego powinno się badać wszystkie funkcje. W niektórych przypadkach potrzebne są dodatkowe informacje, a niektóre są zbędne, albo nawet nie dają się wyliczyć. W trakcie wyliczania może się okazać, że potrzebne są dodatkowe wartości w różnych punktach przedziałów, czy wartości pochodnych wyższych rzędów.
Przykłady
Przykład 1. Narysować wykres funkcji 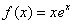 .
.
Dziedziną funkcji 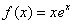 jest zbiór liczb rzeczywistych.
jest zbiór liczb rzeczywistych.
Funkcja nie jest: parzysta, nieparzysta, okresowa.
Wykres funkcji przecina osie układu współrzędnych w punkcie (0,0)
Funkcja f(x) jest ciągła na całej dziedzinie.
Obliczmy wartości w 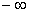 i w
i w 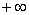 :
:
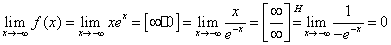
oraz
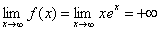 .
.
Ponieważ f(x) jest ciągłą funkcją, stąd jej wykres nie ma asymptot pionowych, które występują tylko w miejscach nieciągłości funkcji. Z obliczonej granicy w minus nieskończoności widać, ze wykres funkcji ma asymptotę poziomą lewostronną y = 0.
Sprawdzimy teraz, czy wykres funkcji ma asymptotę ukośną:
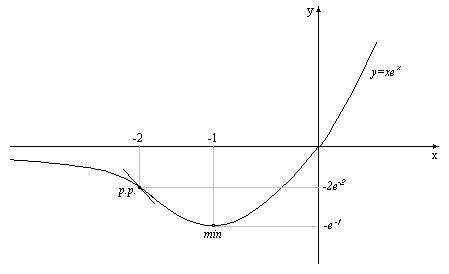
Rys. 1
Ponieważ mamy:
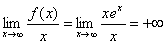 ,
,
stąd mamy, że nie istnieje asymptota ukośna (pozioma) prawostronna.
Obliczamy pierwszą pochodną f(x), mamy:
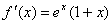 .
.
Zatem funkcja f(x) rośnie, gdzie 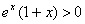 , czyli gdy
, czyli gdy  . Natomiast dla
. Natomiast dla 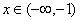 funkcja f(x) maleje. Stąd wynika, że dla x = -1 funkcja osiąga minimum:
funkcja f(x) maleje. Stąd wynika, że dla x = -1 funkcja osiąga minimum: 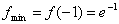 .
.
Obliczamy drugą pochodną funkcji f(x), mamy:
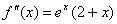 .
.
Druga pochodna jest dodatnia gdy 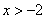 . Co znaczy, że dla
. Co znaczy, że dla 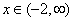 funkcja f(x) jest wypukła, a dla
funkcja f(x) jest wypukła, a dla 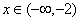 funkcja f(x) jest wklęsła. Stąd wynika, że punkt
funkcja f(x) jest wklęsła. Stąd wynika, że punkt 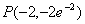 jest punktem przegięcia.
jest punktem przegięcia.
Sporządzamy tabelę zmienności funkcji:
|
x
|
|
-2
|
(-2,-1)
|
-1
|
(-1,0)
|
0
|
|
|
|
-
|
-
|
-
|
0
|
+
|
+
|
+
|
|
|
-
|
0
|
+
|
+
|
+
|
+
|
+
|
|
|
0(
|
p. p.
|
(
|
min
|
&
|
0
|
|
Wykres został przedstawiony na rysunku nr 1.
Przykład 2. Narysować wykres funkcji:
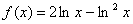 .
.
Dziedziną funkcji jest zbiór liczb rzeczywistych dodatnich.
Miejsca zerowe wyznaczymy z równania:
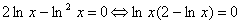 .
.
Stąd miejscami zerowymi są punkty: 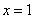 lub
lub 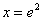 .
.
Obliczmy wartości w 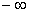 i w
i w 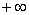 :
:

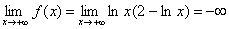 .
.
Stąd mamy, że prosta x = 0 jest asymptotą pionową wykresu funkcji y = f(x),
Nie istnieje asymptota pozioma.
Nie istnieje też asymptota ukośna prawostronna, bowiem mamy:
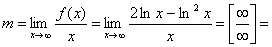
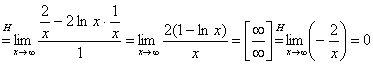 ,
,
co by znaczyło, iż istnieje asymptota, której, jak wiadomo nie ma, bowiem mamy:
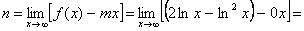
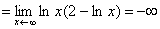 .
.
Obliczamy pierwszą pochodną funkcji f(x), mamy:
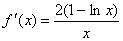 .
.
Pochodna funkcji ma 1 miejsce zerowe w punkcie x = e, ponadto:
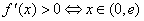 ,
,
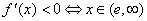 .
.
Stąd wynika, że funkcja jest rosnąca, gdy 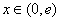 , a malejąca gdy
, a malejąca gdy 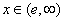 .
.
Co znaczy, że dla x = e funkcja osiąga maksimum: 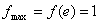 .
.
Obliczamy drugą pochodną funkcji f(x), otrzymamy:
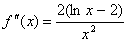 .
.
Pierwsza pochodna równa jest zero dla 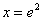 oraz:
oraz:
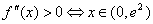 i
i 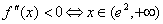 .
.
Znaczy to, że w przedziale 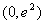 funkcja f(x) jest wypukła, a w przedziale
funkcja f(x) jest wypukła, a w przedziale 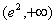 jest wklęsła. Stąd wynika, że punkt
jest wklęsła. Stąd wynika, że punkt 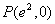 jest punktem przegięcia wykresu funkcji.
jest punktem przegięcia wykresu funkcji.
Sporządzając tabelę zmienności funkcji, dostaniemy:
|
x
|
(0,1)
|
1
|
(1,
|
|
(
|
|
(
|
|
|
+
|
+
|
+
|
0
|
-
|
-
|
-
|
|
|
-
|
-
|
-
|
-
|
-
|
0
|
+
|
|
|
-
|
0
|
&
|
1
max
|
(
|
0
p.p.
|
|
Wykres funkcji 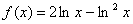 został przedstawiony na rysunku 2.
został przedstawiony na rysunku 2.
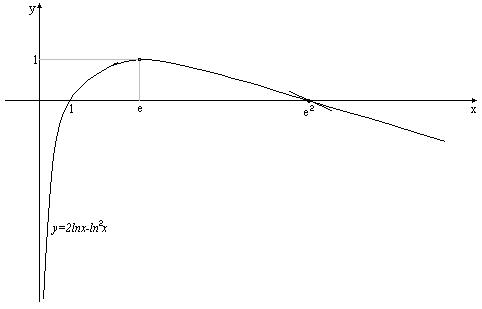
Rys. 2
Przykład 3. Zbadać funkcję:
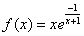 .
.
Dziedziną tej funkcji jest zbiór Df =R{1}. Badajmy granice na końcach przedziału określoności, dostaniemy:
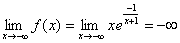 ,
,
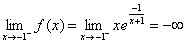 ,
,
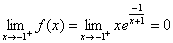 ,
,
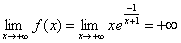 .
.
Z drugiej granicy wynika, że wykres naszej funkcji ma asymptotę pionową lewostronną o równaniu x = -1. Szukamy asymptot ukośnych, stąd mamy:
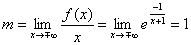 ,
,
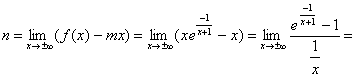
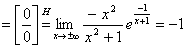 .
.
Stąd wynika, że wykres naszej badanej funkcji ma dwustronną asymptotę ukośną, która ma równanie:
y = x - 1.
Obliczamy pierwszą pochodną funkcji f(x), dostaniemy:
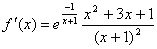 .
.
Równanie 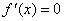 ma dokładnie 2 pierwiastki:
ma dokładnie 2 pierwiastki:
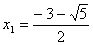 ,
, 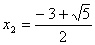 .
.
Patrząc na znak pierwszej pochodnej, stwierdzimy, że nasza badana funkcja jest funkcją rosnącą w przedziałach 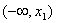 oraz
oraz 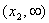 oraz malejącą w przedziałach
oraz malejącą w przedziałach 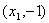 oraz
oraz 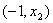 . W punkcie
. W punkcie 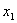 funkcja f(x) osiąga maksimum
funkcja f(x) osiąga maksimum 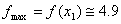 , a w punkcie
, a w punkcie  minimum
minimum 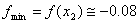 .
.
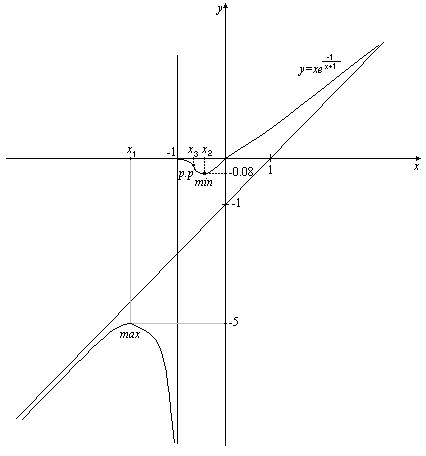
Rys. 3
Obliczamy druga pochodną funkcji f(x), dostaniemy:
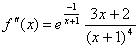 .
.
Równanie 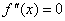 ma dokładnie 1 pierwiastek
ma dokładnie 1 pierwiastek 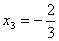 , przy czym
, przy czym 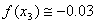 , a ponadto:
, a ponadto:
 ,
,
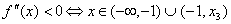 .
.
Znaczy to, że w przedziale 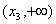 funkcja f(x) jest wypukła, a w przedziałach
funkcja f(x) jest wypukła, a w przedziałach 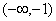 oraz
oraz 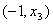 jest ona wklęsła. Stąd wynika, że punkt
jest ona wklęsła. Stąd wynika, że punkt 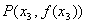 jest punktem przegięcia wykresu naszej badanej funkcji.
jest punktem przegięcia wykresu naszej badanej funkcji.
Sporządzamy tabelkę przebiegu zmienności funkcji, otrzymamy:
|
x
|
|
|
(
|
-1
|
(-1,
|
|
(
|
|
|
|
|
+
|
0
|
-
|
x
|
-
|
-
|
-
|
0
|
+
|
|
|
-
|
-
|
-
|
x
|
-
|
0
|
+
|
+
|
+
|
|
|
|
-4.9
max
|
|
x
|
0(
|
-0.03
p. p.
|
|
-0.08
min
|
|
Wykres funkcji 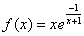 został przedstawiony na rysunku 3.
został przedstawiony na rysunku 3.

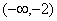
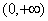
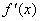
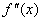
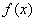
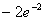
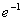
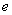 )
)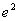 )
)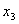 )
)