Momenty w fizyce

1. Moment

Momenty - są to pierwsze człony grupy wielkości fizycznych wykorzystywanych w fizyce, mechanice oraz wytrzymałości substancji. Są wykorzystywane, gdy mamy do czynienia z ruchem nieprostoliniowym. Mogą posiadać przeróżne jednostki. Często są w odmianach: względem punktu (bieguna) M_o albo względem prostej (osi) M_l. M. in. wyróżniamy

momenty: pędu L, siły M, masowy J, pola, linii.

Przykłady momentów (M.):

• M. posiadające jednostkę SI: m.N = N.m = kg.m²/s² = kg.m².s^-2 (m.in.: zginający, skręcający)
  • Moment siły (albo układu sił - Moment główny) względem punktu
  • M. siły względem osi
• M. posiadający jednostkę: m.(kg.m/s) = kg.m²/s. Jest to Moment pędu czyli kręt. Może być spinowy, nazywany spinem(albo orbitalny)
• M. posiadający jednostkę: kg.m². Jest to tzw. masowy Moment bezwładności albo Moment bezwładności ciała względem osi
• M. posiadające jednostkę: m⁴. Są to tzw. Moment bezwładności figury względem: osi lub bieguna
• M. posiadający jednostkę m³. Jest to tzw. Moment statyczny linii względem osi
• M. posiadający jednostkę m². Jest to tzw. Moment statyczny pola względem osi

2. Moment bezwładności

Moment bezwładności, miara bezwładności ciała w ruchu obrotowym. Cechuje rozkład masy w ciele. Moment bezwładności ciała względem osi z nazywa się jest wyrażenie:

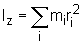
gdzie m_i - masy elementów ciała odległe każda o r_i od osi z

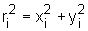
Dla ciągłego rozkładu masy w ciele sztywnym moment bezwładności określany jest wzorem całkowym:

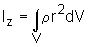
gdzie: ρ - funkcja definiująca gęstość ciała, V - objętość ciała, dV - fragment objętości, r - odległość elementu dV od osi z.

Energia w ruchu obrotowym ciała sztywnego zdefiniowana jest wzorem: E=(Iω²)/2. Moment bezwładności względem osi z' równoległej do z, odległej od niej o D wyraża się wzorem:

I_z=I_z'+MD²

gdzie: M - masa ciała, jest to tzw. twierdzenie Steinera, podane przez matematyka szwajcarskiego J. Steinera.

Określenia powyższego momentu bezwładności są wielkościami skalarnymi, w ogólnym przypadku moment bezwładności jest tensorem trzeciego rzędu, wyrazy na przekątnej (w reprezentacji macierzowej tensora) są momentami bezwładności wyliczone względem trzech wzajemnie prostopadłych osi przedmiotu, np.:

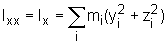
albo - dla ciągłego rozkładu masy - odpowiedni wzór całkowy), wyrazy poza przekątną nazywa się momentami odśrodkowymi określone są następująco (albo przez odpowiednie wzory całkowe):

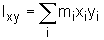
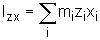
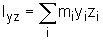
Gdy znamy składowe tensora momentu bezwładności możemy wyliczyć moment bezwładności względem jakiejkolwiek prostej l przechodzącej przez początek układu współrzędnych x,y,z, wtedy:

I_l=I_xxα²+I_yyβ²+I_zzγ-2I_xyαβ-2I_yzβγ-2I_zxγα

3. Wyznaczanie momentu bezwładności przy pomocy urządzenia Hartle'a

WSTĘP TEORETYCZNY

Do opisu ruchu obrotowego bryły sztywnej . trzeba uwzględnić wielkości nieistotne przy definiowaniu ruchu postępowym ciała. W tym wypadku bowiem rozmiary bryły, przestrzenny rozkład masy jak również oś, względem której może się ona obracać odgrywają bardzo ważne znaczenie. I dlatego:

• do zdefiniowania bezwładności bryły nie wystarczy podać jedynie jej masy, ale trzeba określić moment bezwładności I
• wszystkie punkty obracającej się bryły posiadają inną prędkość liniową, więc niezbędne staje się wprowadzenie pojęcia prędkości kątowej , która jest wspólna dla całej bryły.
• energia kinetyczna obracającej się bryły uzależniona jest nie tylko od masy ciała ale także od prędkości przemieszczania się środka masy bryły, ale także od prędkości kątowej bryły oraz jej momentu bezwładności względem osi obrotu.

Gdy będziemy korzystać z definicji momentu bezwładności możemy, bez większego trudu, wyprowadzić wzór na moment bezwładności dla wielu regularnych brył, szczególnie dla jednorodnych brył obrotowych. Także w literaturze możemy zobaczyć przykłady takich wzorów. Ale, by wyznaczyć moment bezwładności konkretnego ciała, trzeba uciec się przede wszystkim do eksperymentu. Przykładem urządzenia, które wykorzystywane jest do eksperymentalnego wyznaczenia momentu bezwładności jest urządzenie Hartle'a.

CEL ĆWICZENIA

Celem ćwiczenia jest wyznaczenie momentu bezwładności wielu tarcz metalowych oraz sprawdzenie czy uzyskane wyniki są zgodne z obliczeniami na podstawie teoretycznego wzoru.

METODA POMIAROWA

Układ pomiarowy złożony jest z:

• umieszczonego na poziomej osi bloku A, na który nawinięta jest nić
• zestawu metalowych tarcz B, które można umieszczać na osi bloku A
• dwóch odważników o zmierzonych wcześniej masach m₁
• oraz m₂, powieszonych na końcu nici oraz wprawiających w ruch obrotowy blok oraz analizowane tarcze,
• podziałki milimetrowej wykorzystywanej do pomiaru drogi przebywanej przez opadający ciężarek,

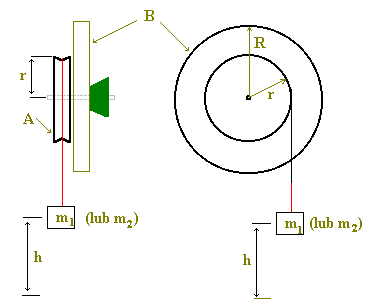
• układu elektronicznego pomiaru czasu trwania ruchu o dokładności 0,01s.

Pomysł pomiaru polega na zamianie energii potencjalnej odważnika (zawieszonego na nici nawiniętej na bloku oraz opadającego na skutek siły ciężkości) na energię kinetyczną. Na tę energię kinetyczną składa się energia kinetyczna ruchu postępowego odważnika oraz energia kinetyczna ruchu obrotowego bloku z tarczą. Część tej energii potencjalnej jest, niestety, wykorzystana na dokonanie pracy przeciwko siłom tarcia T. By wyeliminować tę, niewygodną do obliczenia, stratę, dokonujemy dla każdej tarczy pomiarów przy zastosowaniu dwóch różnych odważników o zmierzonych wcześniej masach m₁ oraz m₂. Oznaczając odpowiednio symbolami:

E_ko -energię kinetyczną odważnika na nitce,

E_kb -sumę energii kinetycznej bloku z nicią oraz tarczy

E_p -energię potencjalną odważnika na nitce,

W_T -pracę sił tarcia hamującego ruch (tarcie w osi bloku, tarcie nici o blok itp.),

Zasadę zachowania energii możemy zatem zapisać dla tego układu w następujący sposób:

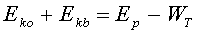
Podstawiając odpowiednie wzory oraz uwzględniając to, iż praca sił tarcia przy mało różniących się masach odważników jest praktycznie jednakowa, uzyskamy dla odważników m₁oraz m₂ dwa równania:

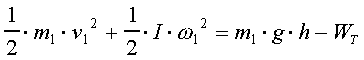
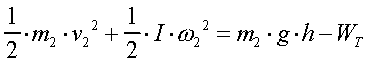
Po odjęciu stronami oraz przekształceniu uzyskamy na moment bezwładności następujący wzór:

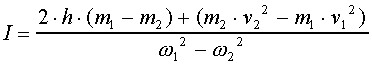
Korzystając ze wzoru na związek prędkości kątowej z liniową:

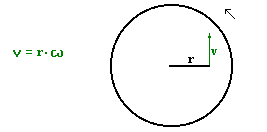
a następnie na drogę ciężarka w ruchu jednostajnie przyspieszonym, z prędkością początkową wynoszącą zero

wyeliminujemy trudne do bezpośredniego pomiaru prędkości v ,uzyskamy ostatecznie następującą zależność:

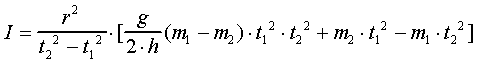
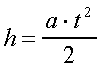
CZYNNOŚCI POMIAROWE

1. Wyznaczamy masy wszelkich analizowanych tarcz
2. Zmierzymy średnice bloku analizowanych tarcz i obliczamy ich promienie (odpowiednio r oraz R)
3. Dla każdej tarczy mierzymy czasy t₁ oraz t₂ opadania ciężarków m₁ oraz m₂ na ustalonym odcinku drogi h. Trzeba pamiętać, by zaczynać pomiary czasu od prędkości początkowej odważnika wynoszącej zero.
4. Pomiary dla każdej tarczy oraz każdego odważnika przeprowadzamy co najmniej trzykrotnie.
5. Pomiary opisane w punkcie 3 należy powtórzyć bez tarcz, by wyznaczyć moment bezwładności bloku oraz pozostałych niezmiennych części układu.