Problemat Leonarda z Pizy. Kto kryje się za tym imieniem?

Problemat Leonarda z Pizy, czyli zagadka o dwóch wieżach, to jedna z legendarnych łamigłówek matematycznych. Po raz pierwszy pojawiła się w księdze napisanej w 1202 roku przez słynnego matematyka (i nie był to Leonardo da Vinci). Dowiedz się o kogo chodzi i jak rozwiązać jego średniowieczną zagadkę!

Spis treści:

Problemat Leonarda. Zagadka o dwóch prostych wieżach
Podpowiedź do zagadki. Rysunek pomocniczy
Rozwiązanie zagadki Leonarda

Problemat Leonarda z Pizy. Zagadka o dwóch prostych wieżach

Zagadkę o dwóch wieżach wymyślił słynny Fibonacci. Taki właśnie pseudonim przyjął Leonardo z Pizy, włoski matematyk z przełomu XII i XIII wieku. Zapisał ją w księdze matematycznej Liber Abaci, tej samej, która stoi za rozpowszechnieniem się w Europie arabskiego zapisu cyfr.

Syn bogatego kupca jest powszechnie uważany za człowieka, w którym po wiekach marazmu odrodziła się europejska matematyka. Jak na ironię najbardziej kojarzy się go jednak z ciągiem Fibonacciego, który w zapisie formalnym nie był odkryciem Leonarda (choć to właśnie on po raz pierwszy posłużył się nim w jednej ze swoich zagadek). W literaturze określenie "ciąg Fibonacciego" pojawiło się dopiero w XIX wieku.

Sprawdź też: Zagadka Diofantosa. Co grecki matematyk pozostawił na swoim nagrobku?

Dziś jednak zajmiemy się łamigłówką, która nie wymaga znajomości żadnego ciągu. Przyda się jednak inne, o wiele starsze twierdzenie. Oto jej treść:

Dwie wieżyce, jedna wysokości 30 stóp, druga 40 stóp, oddalone są od siebie o 50 stóp. Pomiędzy nimi znajduje się wodotrysk, do którego zlatują dwa ptaki z wierzchołków obu wieżyc i lecąc z jednakową prędkością przybywają w tym samym czasie. Jaka jest dłuższa odległość pozioma wodotrysku jednej z wieżyc?

Już wiesz, jak ugryźć to zadanie?

Podpowiedź do zagadki. Rysunek pomocniczy

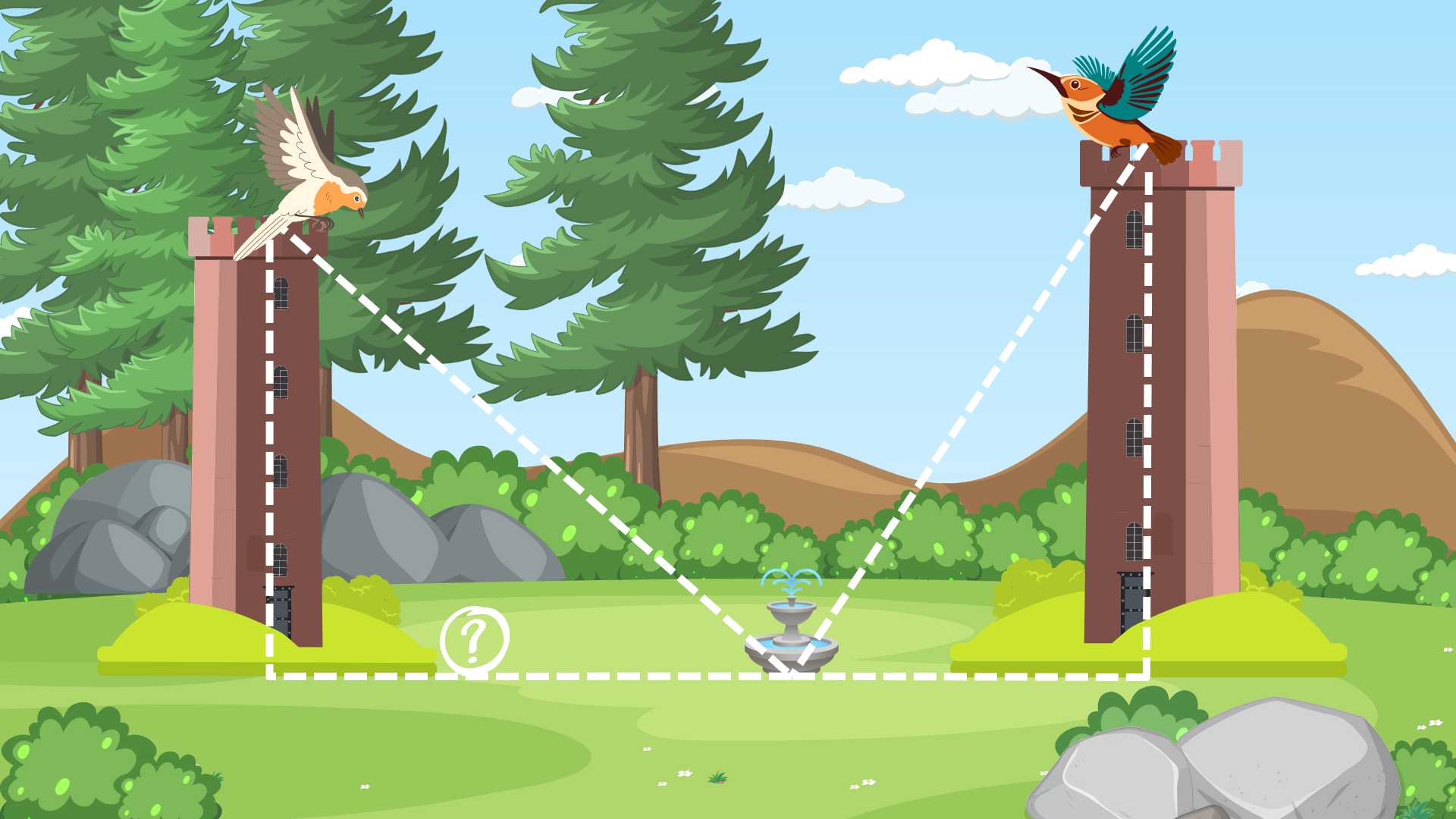
Największą trudność przysparza przełożenie treści zadania na "płótno wyobraźni". Jeśli uda nam się ta sztuka, bardzo szybko zauważymy pewne zależności, a przede wszystkim będziemy dokładnie wiedzieli, co policzyć. Dodatkowym utrudnieniem jest archaiczny język pierwotnej treści zagadki – w końcu spisano ją w 1202 roku. Poniżej, dla ułatwienia, zamieszczamy rysunek pomocniczy z zaznaczonymi odcinkami, które interesują nas w tym zadaniu. Dorzucamy także bardziej współczesny zapis naszej dzisiejszej łamigłówki:

"Dwa ptaki sfruwają jednocześnie ze szczytów dwóch wież, odległych od siebie o 50 stóp. Wysokość jednej wieży wynosi 30 stóp, a drugiej 40 stóp. Lecąc z tą samą prędkością dolatują w tym samym momencie do fontanny, usytuowanej na prostej pomiędzy dwiema wieżami (na poziomie gruntu). W jakiej odległości od podstawy bardziej oddalonej wieży znajduje się fontanna"?

problemat leonarda dwie wieże w pizie rysunek pomocniczy — **W tym zadaniu naszym "iksem" jest odległość między fontanną a niższą wieżą** /fot. Canva Pro

Przeczytaj: Dawne miary i wagi. Ile ważył centar i czym była wielka seta?

Rozwiązanie zagadki Leonarda

Mamy nadzieję, że dzięki podpowiedziom wszyscy, którzy zmierzyli się z zagadką znają już prawidłową odpowiedź. Sprawdźmy, czy wszystko się zgadza.

Na rysunku pomocniczym widać jak na dłoni, że poszczególne odcinki tworzą trójkątny prostokątne. Bez wątpienia przy rozwiązaniu będziemy musieli skorzystać z twierdzenia Pitagorasa.

Naszym zadaniem jest obliczenie długości jednej z przyprostokątnych – odcinka między fontanną a podstawą niższej wieży.

Oznaczmy odległość poziomą od pierwszej wieży (o wysokości 30 metrów) do fontanny jako x.
Oznaczmy odległość poziomą od drugiej wieży (o wysokości 40 metrów) do fontanny jako y.
Z treści zagadki wiemy, że suma tych odległości wynosi 50 metrów: x+y=50

Twierdzenie Pitagorasa mówi, że suma kwadratów długości przyprostokątnych trójkąta prostokątnego jest równa kwadratowi długości przeciwprostokątnej tego kwadratu, czyli: c²= a²+ b²

Ponieważ oba ptaki lecą z tą samą prędkością i docierają w tym samym momencie, długości ich tras (c) muszą być równe:

x²+30²= y²+40²

Po wyliczeniu kwadratów wartości liczbowych otrzymujemy: x² +900 = y² +1600; a wiedząc, że x+y = 50, możemy zapisać to równanie jako:

x² +900 = (50−x)² +1600

Rozwinięcie kwadratu po prawej stronie da nam:

x²+900 = 2500−100x+x²+1600

Na pierwszy rzut oka widać, że po przeniesieniu "iksów" na jedną stronę te z kwadratami ulegną skróceniu. Gdy porachujemy wartości liczbowe otrzymamy:

100x = 3200

x = 3200:100

x = 32

W ten sposób dochodzimy do rozwiązania XIII-wiecznej zagadki Leonarda z Pizy. Dłuższa odległość pozioma między wieżą i fontanną ma 32 stopy (a krótsza 18, co w sumie daje nam 50 stóp).