1. Cel ćwiczenia.
Celem ćwiczenia było zapoznanie się z działaniem kodu "ilorazowego". W tym celu wykorzystaliśmy symulator "Laboratorium kodowania i transmisji danych" badając słuszność założeń działania kodu.
2. Wstęp teoretyczny.
Jak wiadomo liczba zapisana w kodzie dwójkowym stanowi ciąg "0" i "1". Korzystając z opisu liczby binarnej za pomocą kodu ilorazowego mamy możliwość zapisania dowolnej liczby dwójkowej za pomocą wielomianu stopnia n-1. Wykładniki odpowiadają wówczas numerom pozycji, natomiast współczynniki przy x przyjmują wartości {0,1}.
Nasza liczba binarna zapisana pod postacią wielomianu będzie wyglądała następująco:
a(x) = a0 + a1x + a2x2 + a3x3 + ... + anxn
gdzie al = {0,1} (a0, a1, a2, .., an)
Operacje na ciągach kodowych można zatem sprowadzić do działań na wielomianach. Mnożenia i dzielenia dokonuje zgodnie z prawami algebry, a dodawanie i odejmowanie - modulo 2.
Możemy wyodrębnić dwa rodzaje kodów ilorazowych: kody systematyczne oraz kody niesystematyczne. Główną przyczyną powstania kodów ilorazowych, czyli kodów opartych na kryterium podzielności była prostota realizacji mnożenia i dzielenia ciągów.
Zgodnie z instrukcją zawartą w wykorzystanym programie możemy zdefiniować:
h(x)- wielomian związany z ciągiem informacyjnym
s(x)- wielomian związany z ciągiem kodowym
g(x)- wielomian generujący w postaci:
g(x)=xp+g[p-1]∙xp-1+g[p-2]∙xp-2+…+g[1]∙x+g[0]
gdzie: g[0], g[1], ..., g[p-1], 1 - ciąg cyfr binarnych
2. Analiza kodu ilorazowego niesystematycznego.
Na wstępie podczas kodowania wielomian związany z ciągiem informacyjnym h(x), jest przemnażany przez wielomian generujący g(x). W wyniku tej operacji otrzymujemy wielomian wyjściowy s(x). Stanowi on zakodowaną informację która po przejściu przez kanał dociera do dekodera. Dekoder dzieli otrzymany wielomian przez g(x) i sprawdza czy po podzieleniu zostaje jakaś reszta r(x). Jeśli tak to znaczy ze nastąpił błąd w kanale i ciąg informacyjny zawiera błędy. Jeśli r(x)=0 to ciąg h(x) jest poprawny, lub nastąpił błąd niemożliwy do wykrycia.
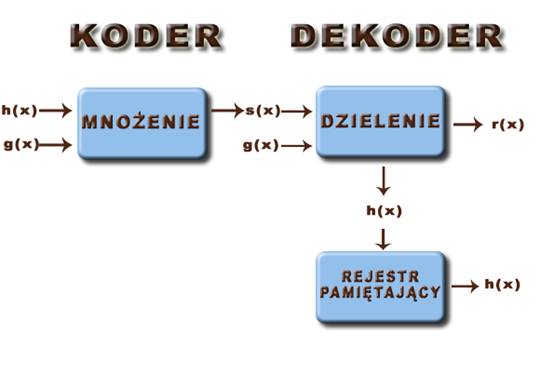
Schemat budowy kodera i dekodera dla kodu niesystematycznego ilorazowego
Poniżej przedstawiamy kilka przykładów kodu ilorazowego niesystematycznego oraz ich rozwiązania analityczne.
|
Ciąg informacyjny h(x)
|
Ciąg generacyjny g(x)
|
Ciąg kodowy/wyjściowy s(x)
|
|
10
|
101
|
1010
|
|
11101
|
1011
|
11001111
|
|
110110
|
10101
|
1110001110
|
|
1111
|
10111
|
11011101
|
Dla przykładu pierwszego: Dla przykładu drugiego: Dla przykładu trzeciego:
g(x) 101 h(x) 11101 h(x) 110110
h(x) * 10 g(x) * 1011 g(x) * 10101
-------------- ------------ ---------------
000 11101 110110
+ 101 11101 000000
-------------- 00000 110110
s(x) 1010 + 11101 000000
------------ + 110110
Dla przykładu czwartego: 11001111 ---------------
g(x) 10111 1110001110
h(x) * 1111
------------
10111
10111
10111
+ 10111
------------
11011101
2. Analiza kodu ilorazowego systematycznego.
Aby otrzymać kod ilorazowy systematyczny (informacja jest na początku, a pozycje kontrolne na końcu ciągu kodowego) stosuje się inną metodę kodowania. Na wyjściu kodera tworzymy następujący wielomian s(x)=xp∙h(x)-R(x), gdzie R(x) jest wielomianem stanowiącym resztę uzyskaną z podzielenia wielomianu: xp∙h(x), przez wielomian generujący g(x). Na dekoder składa się z kolei k-komórkowy rejestr (zapamiętanie odebranego ciągu informacyjnego h'(x)), układ dzielący (wyznacza resztę R"(x) z podziału h'(x) przez g(x)) oraz układ porównujący resztę R"(x) z odebraną resztą R'(x). Jeżeli reszty R"(x) i R'(x) są jednakowe, informacja odebrana została bezbłędnie, lub wystąpił błąd niewykrywalny.
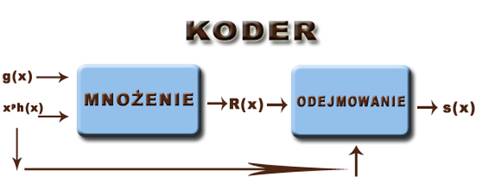
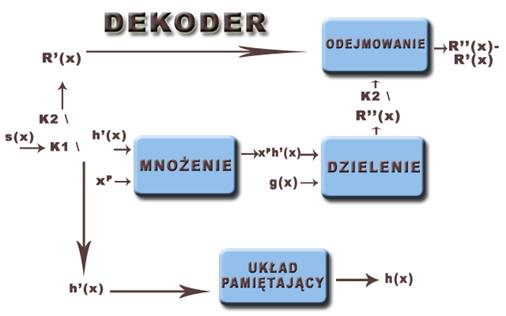
Schemat budowy kodera i dekodera dla kodu niesystematycznego ilorazowego.
|
Ciąg informacyjny h(x)
|
Ciąg generacyjny g(x)
|
Ciąg kodowy/wyjściowy s(x)
|
|
01111
|
10100
|
011110000
|
|
01000
|
11010
|
010000010
|
|
11001
|
10011
|
110011101
|
|
00001
|
11001
|
000011001
|
Tabelka powyżej przedstawia przykłady dla kodu ilorazowego systematycznego. Teraz postaramy się opisać jak tworzony jest opisywany kod na jednym z przykładów. Żeby otrzymać ciąg kodowy, tworzę uprzednio pomocniczy ciąg o długości h(x)+g(x)-1 (w tym przypadku h(x) i g(x) to długość słowa bitowego). Pierwszą pozycję tego ciągu zajmie ciąg informacyjny, pozostałą część uzupełnię zerami. Taki otrzymany ciąg dzielę przez ciąg generacyjny aż do otrzymania reszty. Ostatnią część reszty uzupełniam mój ciąg informacyjny do uzyskania pożądanej długości ciągu kodowego (to jest h(x) + g(x) -1 ).
x^4 x^3 x^1 x^0
----------------
(x^8 x^7 x^4 ) : (x^4 x^1 x^0)
+ x^8 x^5 x^4
--------------
x^7 x^5
+ x^7 x^4 x^3
------------------
x^5 x^4 x^3
+ x^5 x^2 x^1
----------------------
x^4 x^3 x^2 x^1
+ x^4 x^1 x^0
------------------------------
r x^3 x^2 x^0 à 1101
np. h(x)=11001 |h(x)|=5 |g(x)|=5 więc nasz ciąg pomocniczy ma długość |h(x)|+|g(x)|- -1=9. Wygląda on tak: 110010000. Zamieniam go na postać wielomianową, to jest: x^8+x^7+x^4 i dzielę go przez g(x) ( x^4+x^1+x^0). Otrzymaną resztę dodaję do mojego ciągu informacyjnego otrzymując w ostateczności 110011101.
2. Zastosowania i wnioski końcowe.
W przeprowadzonym ćwiczeniu mieliśmy okazję zapoznać się z zasadą działania kodu ilorazowego systematycznego i niesystematycznego. Ze względu na swoją prostotę i duży współczynnik wykrywalności błędów kody ilorazowe znalazły powszechne zastosowanie w telekomunikacji. Przedstawione w sprawozdaniu schematy koderów i dekoderów nie stanowią dużego wyzwania dla projektantów, co sprawia, że ich realizacja za pomocą standardowych elementów jest bardzo prosta.
Kody ilorazowe stosuje się między innymi w przypadku liczenia sum kontrolnych CRC (Cyclic Redundancy Code). Od stosowanej czasami sumy danych (suma wszystkich bajtów lub słów bloku sumowanych danych) różni ten algorytm jego znacznie większa niezawodność wykrywania błędów. CRC jest odporny na zmianę kolejności bajtów, nie wykrywaną przez sumę. Podstawowym elementem algorytmu jest wielomian generacyjny (generator). Rozmiar sumy kontrolnej zależy od stopnia tego wielomianu. Oto kilka popularnych wielomianów:
CRC-12: x^12 + x^11 + x^3 + x^2 + x^1 + 1
CRC-16: x^16 + x^15 + x^2 + 1
ETHERNET: x^32 + x^26 + x^23 + x^22 + x^16 + + x^12 + x^11 + x^10 + x^8 + x^7 + + x^5 + x^4 + x^2 + x^1 + 1
Prawdopodobieństwo wykrycia błędu przy użyciu CRC-16:
- 100 proc. w przypadku błędów pojedynczych, podwójnych, seryjnych (seria nie dłuższa niż 16 bitów), z nieparzystą liczbą bitów,
- 99,997 proc. dla błędów seryjnych 17-bitowych,
- 99,998 proc. dla błędów seryjnych 18-bitowych i dłuższych.
Dla kodu ETHERNET wartości te są następujące:
- wszystkie błędy seryjne, o długości nie przekraczającej 32 bitów są wykrywane;
- prawdopodobieństwo nie wykrycia błędu seryjnego 33-bitowego wynosi 2^(-31);
- prawdopodobieństwo nie wykrycia błędu seryjnego 34-bitowego lub dłuższego - 2^(-32).
Jak widać w przykładach powyżej zastosowanie odpowiednich wielomianów generujących zapewnia praktycznie 100% pewność wykrycia błędu. W przypadku analizowanych kodów stałowagowych "2 z 5" oraz "3 z 7" prawdopodobieństwa niewykrycia błędu były zauważalnie większe, co przemawia za stosowaniem kodów ilorazowych.


