I. Wstęp
Kod "2 z 5" jest kodem detekcyjnym 5-bitowym. Na 5 bitów w których kodowany jest jeden znak, występują 2 jedynki, jest to zatem kod stałowagowy. Pamiętając o podanych zasadach tworzenia kodu, można w nim zakodować 10 znaków. Minimalna odległość Haminga wynosi 2.
Zaletą stosowania kodu "2 z 5" jest prosta budowa kodera i dekodera. W ich skład wchodzą bramki NAND i NOT. Koder składa się z dziesięciu wejść (odpowiadającym cyfrom 0-9 ) oraz pięciu wyjść (z których składany jest pięciobitowy kod). Dekoder jest zbudowany odwrotnie do kodera - pięć wejść i dziesięć wyjść.
Kody poszczególnych znaków:
|
Słowo kodowane
|
Otrzymany kod
|
|
0
|
11000
|
|
1
|
10100
|
|
2
|
10010
|
|
3
|
10001
|
|
4
|
01100
|
|
5
|
01010
|
|
6
|
01001
|
|
7
|
00110
|
|
8
|
00101
|
|
9
|
00011
|
II. Analiza działania dekodera
Po zapoznaniu się z działaniem programu postanowiłem przeanalizować działanie dekodera dla cyfry 7, której odpowiada kod: 00110. Zakodowana w ten sposób informacja jest zgodna z później przeprowadzoną symulacją, co potwierdza poprawność budowy kodera. Analizę detekcji przedstawiają poniższe tabelki:
- Błąd pojedynczy
|
Otrzymany kod
|
Odpowiedź dekodera
|
|
10110
|
błąd
|
|
01110
|
błąd
|
|
00010
|
błąd
|
|
00100
|
błąd
|
|
00111
|
błąd
|
Zmiana jednego bitu powoduje zmianę liczby jedynek w kodzie, która po każdym z błędów jednokrotnych jest różna od 2. Dekoder prawidłowo rozpoznaje otrzymany kod jako błędny. Wszystkie błędy są zatem wykrywane.
- Błąd podwójny
|
Otrzymany kod
|
Odpowiedź dekodera
|
|
11110
|
błąd
|
|
10010
|
2
|
|
10100
|
1
|
|
10111
|
błąd
|
|
01010
|
5
|
|
01100
|
4
|
|
01111
|
błąd
|
|
00000
|
błąd
|
|
00011
|
9
|
|
00101
|
8
|
W tym wypadku, jeżeli w wyniku zakłócenia kodu na 2 bitach, otrzymamy liczbę jedynek równą 4, bądź 0, błąd zostanie wykryty. Jeżeli jednak przekłamaniu ulegnie jeden bit który jest jedynką, i jeden który nią nie jest, otrzymamy kod 5 bitowy z wagą 2. Zgodnie z logiką dekoder błędnie dekoduje otrzymaną informację, jako inne słowo. W przypadku błędu podwójnego dekoder wychwytuje 40% błędów.
- Błąd potrójny
|
Otrzymany kod
|
Odpowiedź dekodera
|
|
11010
|
błąd
|
|
11100
|
błąd
|
|
11111
|
błąd
|
|
10000
|
błąd
|
|
10011
|
błąd
|
|
10101
|
błąd
|
|
01000
|
błąd
|
|
01011
|
błąd
|
|
00001
|
błąd
|
|
10011
|
błąd
|
Podobnie jak w przypadku błędu jednokrotnego zmiana trzech bitów powoduje zmianę liczby jedynek w kodzie, która po każdym z błędów potrójnych jest różna od 2. Dekoder prawidłowo rozpoznaje otrzymany kod jako błędny. Wszystkie błędy są zatem wykrywane.
- Błąd poczwórny
|
Otrzymany kod
|
Odpowiedź dekodera
|
|
01001
|
6
|
|
10001
|
3
|
|
11101
|
błąd
|
|
11011
|
błąd
|
|
11000
|
0
|
Podobnie jak w wypadku błędu podwójnego, jeżeli w wyniku zakłócenia kodu na 4 bitach, otrzymamy liczbę jedynek równą 4, błąd zostanie wykryty. Jeżeli jednak przekłamaniu ulegną 2 bity które są jedynką i 2 które nią nie są, otrzymamy kod 5 bitowy z wagą 2. Zgodnie z logiką dekoder, błędnie dekoduje otrzymaną informację, jako inne słowo. W przypadku błędu podwójnego dekoder wychwytuje 40% błędów.
- Błąd pięciokrotny
|
Otrzymany kod
|
Odpowiedź dekodera
|
|
11001
|
błąd
|
Zmiana 5 bitów powoduje zmianę liczby jedynek w kodzie, błąd jest zatem wykrywalny.
Reasumując kod "2 z 5" posiada dość dużą skuteczność: pozwala na całkowite wyeliminowanie błędów nieparzystych oraz 40% błędów parzystych. Wysoką skuteczność opisywany kod zawdzięcza temu, że jest stałowagowy.
Możemy obliczyć prawdopodobieństwo niewykrycia błędu przez dekoder. Zgodnie z przeprowadzoną analizą działania dekodera wnioskuję, że błąd może nie zostać wykryty jedynie w dwóch wypadkach:
- zakłócenie wystąpiło na 2 bitach, przy czym wynik ograniczamy do wyboru jednego bitu spośród dwóch jedynek oraz jednego bitu spośród trzech zer
- zakłócenie wystąpiło na 4 bitach, przy czym wynik ograniczamy do wyboru dwóch bitów spośród dwóch jedynek oraz dwóch bitów spośród trzech zer
Korzystając ze schematu Bernoulliego otrzymałem następujący wynik:
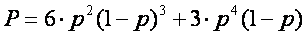
Zakładając, że prawdopodobieństwo przekłamania jednego bitu jest równe p=½, otrzymujemy następujące rezultaty:
- prawdopodobieństwo niewykrycia błędu wynosi P = 28,1%
- prawdopodobieństwo wykrycia błędu wynosi P'=71,9%
Prawdopodobieństwo wykrycia błędu nieparzystego jest zawsze równe 100%. Prawdopodobieństwo, że w kodzie wystąpi konkretna liczba zakłóceń również otrzymamy ze schematu Bernoulliego, np. prawdopodobieństwo dokładnie dwóch przekłamań wynosi:
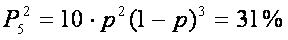
III. Analiza kodu "3 z 7"
Kod "3 z 7" jest kodem analogicznie do kodu "2 z 5" jest kodem stałowagowym, z wagą 3, w którym do kodowania użyto 7 bitów. Chcąc policzyć ilość możliwych do zakodowania znaków używam kombinacji 3 z 7 (miejsc na których można postawić jedynkę), otrzymując wynik 35.
Będę starał się porównać oba kody pod względem prawdopodobieństwa niewykrycia błędu. Kod "3 z 7" można wykorzystać zarówno dla wszystkich 35 możliwych do zakodowania słów lub do zakodowania 10 cyfr, podobnie jak w kodzie "2 z 5".
- Wykorzystane jest wszystkie 35 znaków
Podobnie jak w kodzie "2 z 5" rozpatrzę możliwości przekłamań, oraz skuteczności wykrywania błędów w zależności od liczby zakłóconych bitów:
- wszystkie nieparzyste błędy są wychwytywane
- 2 bity można zakłócić na 21 sposobów, z czego 9 posiada przekłamanie liczby jedynek, skuteczność wykrywania błędów wynosi zatem 42,8%
- 4 bity można zakłócić na 35 sposobów, z czego 17 posiada przekłamanie liczby jedynek, skuteczność wykrywania błędów wynosi zatem 48,6%
- 6 bitów można zakłócić na 7 sposobów, z czego 3 posiada przekłamanie liczby jedynek, czyli skuteczność wykrywania błędów wynosi 42,8%
Analogicznie jak w przypadku kodu "2 z 5" korzystając ze schematu Bernoulliego wyliczam wzór na prawdopodobieństwo niewykrycia błędu:
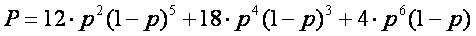
Zakładając, że prawdopodobieństwo przekłamania jednego bitu jest równe p=½, otrzymujemy następujące rezultaty:
- prawdopodobieństwo niewykrycia błędu wynosi P = 25,8%
- prawdopodobieństwo wykrycia błędu wynosi P'=74,2%
- Wykorzystane jest 10 znaków
Zakładam że dekoder potrafi rozpoznać 10 spośród 35 wykorzystanych przez nas możliwości i jeżeli otrzyma liczbę odpowiadającą np. 17, uzna ją za błąd. Rozpatruję możliwości przekłamań, oraz skuteczności wykrywania błędów w zależności od liczby zakłóconych bitów:
- wszystkie nieparzyste błędy są wychwytywane
- 2 bity można zakłócić na 21 sposobów, z czego 9 posiada przekłamanie liczby jedynek, czyli 42,8%. Z pozostałych 12 możliwości tylko 9 może przechowywać jakąś cyfrę, minimalna skuteczność kodu wynosi zatem 57,1%, a maksymalna 100%, średnia skuteczność wynosi 78,5%
- 4 bity można zakłócić na 35 sposobów, z czego 17 posiada przekłamanie liczby jedynek, czyli 48,6%. Z pozostałych 18 możliwości tylko 9 może przechowywać jakąś cyfrę, minimalna skuteczność kodu wynosi zatem 74,2%, a maksymalna 100%, średnia skuteczność wynosi około 87,1%
- 6 bitów można zakłócić na 7 sposobów, z czego 3 posiada przekłamanie liczby jedynek, czyli 42,8%. Ponieważ kodujemy tylko 10 cyfr spośród 35 możliwych, więc skuteczność kodu jest zmienna - od 42,8% do 100%, średnia skuteczność wynosi 71,4%
Analogicznie jak w przypadku kodu "2 z 5" korzystając ze schematu Bernoulliego wyliczam wzór na prawdopodobieństwo niewykrycia błędu:
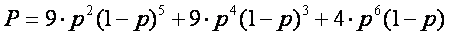
Zakładając, że prawdopodobieństwo przekłamania jednego bitu jest równe p=½, otrzymujemy następujące rezultaty:
- prawdopodobieństwo niewykrycia błędu wynosi P = 17,2%
- minimalne prawdopodobieństwo wykrycia błędu wynosi P'=82,8%
- średnie prawdopodobieństwo wykrycia błędu wynosi około P'= 91,4%
IV. Wnioski
Zastosowanie kodu umożliwiającego wykrycie błędnej transmisji pociąga za sobą zarówno konsekwencje pozytywne (bardzo wysokie prawdopodobieństwo wykrycia błędu w przypadku kodu "3 z 7"), jak i negatywne (zwiększenie ilości bitów na słowo co pociąga za sobą zmniejszenie istotnej szybkości przesyłania danych).
Zestawienie wyników dla obu kodów przedstawia poniższa tabelka:
|
Użyty kod
|
2 z 5
|
3 z 7
|
3 z 7
|
|
Ilość wykorzystanych znaków
|
10
|
10
|
35
|
|
Ilość bitów w kodzie
|
5
|
7
|
7
|
|
Wykrywalność błędów
|
71,9%
|
91,4%
|
74,2%
|
Przy korzystaniu z maksymalnej możliwej ilości znaków dla poszczególnych kodów, nieznacznie lepiej wykrywa błędy kod "3 z 7", jednak ze względu na większą ilość bitów na słowo (aż o 2) jest znacznie wolniejszy. Kod "2 z 5"pozwala zapisać 10 pozycji co idealnie pasuje do kodowania cyfr z kodu dziesiętnego. Jeżeli jednak użyjemy 10 znaków w przypadku kodu "3 z 7", to średnia wykrywalność błędów rośnie zauważalnie. Kod "3 z 7" posiada również tę istotną zaletę, iż umożliwia zakodowanie znaków popularnego kodu szesnastkowego, czego kod "2 z 5" nie jest w stanie nam zapewnić.
Kod "2 z 5" (w licznych odmianach) jest wykorzystywany np. w kodach kreskowych:
Pięć elementów, z których składa się kod "2 z 5 Datalogic" to trzy ciemne i 2 jasne paski. Dwa z nich są szerokie, a trzy wąskie. Cyfra kontrolna może, ale nie musi być dodawana. Graficzne obrazy cyfr przeplatają się Przy pomocy tego kodu można kodować cyfry 0-9.
Kod kreskowy "2 z 5 IATA" jest bardzo popularny. Został zaprojektowany po to by zwiększyć gęstości kodu 2 z 5. Format ten koduje cyfry 0-9. Każda para cyfr reprezentowana jest przez 5 ciemnych i 5 jasnych kresek. Znak startu w tym kodzie to dwa wąskie paski, natomiast znak stopu - jeden szeroki jeden wąski pasek.
