1. Cel ćwiczenia
Celem ćwiczenia było badanie algorytmów: Dijkstry - algorytm najkrótszej drogi, i Dinica - algorytm znajdowania największej dostępnej przepływności pomiędzy użytkownikami. Za pomocą programu "Algorytmy w sieciach telekomunikacyjnych" zbadane zostały ich podstawowe cechy.
2. Wykonanie ćwiczenia
W pierwszej części ćwiczenia korzystając z polecenia "Algorytm - najkrótszej drogi", a następnie "Algorytm - maksymalnego przepływu" zanalizowaliśmy sieci przedstawione w zadanych plikach dijkstra.net, dinic.net. Następnie stworzyliśmy własną sieć i ponownie przeprowadziliśmy zadaną analizę
- Sieć z pliku Dijkstra.net
Analiza algorytmu najkrótszej drogi.
|
TRASA
|
DŁUGOŚĆ DROGI
|
|
1-5-4-6-3
|
23
|
|
1-5-4-6
|
18
|
|
3-1
|
Nie istnieje
|
|
3-4-6
|
13
|
|
6-1
|
Nie istnieje
|
|
6-3
|
5
|
Zbadaliśmy wzajemne relacje między węzłami 1,3,6. Jak widać w tabelce obok nie zawsze połączenie bezpośrednie, jak ma to miejsce w przypadku połączenia między węzłami 3 i 6, jest połączeniem najkrótszym. Widać również że połączenie miedzy dwoma węzłami nie jest sobie równe, dla połączenia 3-6 wynosi 21, natomiast dla połączenia 6-3 wynosi 5. Tą z pozoru dziwną obserwację można w łatwy sposób wytłumaczyć porównując zaistniałą sytuacje do jazdy na rowerze: jeśli zjeżdżamy z górki drodze przypisujemy niższą wagę natomiast jeśli wracamy pod górkę, przypisujemy drodze wyższą wagę.
Analiza algorytmu maksymalnego przepływu.
Z pliku Dijkstra.net zbadaliśmy maksymalny przepływ w sieci między węzłami:
Od 1 do 2 - maksymalny przepływ wynosi 21. Na ten przepływ składają się ścieżki:
1-2 (waga 15), 1-5-2 (waga 4), 1-5-4-6-3-2 (waga 2). Należy zauważyć, że połączenie 1-5 jest wspólne dla dwóch ostatnich ścieżek (waga tego połączenia jest równe 9, z tymże w naszym przypadku, wykorzystujemy tylko 66% "pojemności" tego połączenia (waga 6)).
Od 1 do 5 - maksymalny przepływ wynosi 11. Na ten przepływ składają się ścieżki
1-5 (waga 9), 1-2-4-5 (waga 2). W badanej sieci nie dało się zaobserwować ciekawszych właściwości algorytmu Dinica. Jak widać w podanym przykładzie do maksymalnego przepływu wkład wnoszą jedynie 2 ścieżki, nie korzystające ze wspólnych węzłów.
- Sieć z pliku Dinic.net
Analiza algorytmu najkrótszej drogi.
|
TRASA
|
DŁUGOŚĆ DROGI
|
|
2-5-6
|
130
|
|
2-4-7
|
80
|
|
6-4-2
|
Nie istnieje
|
|
6-7
|
40
|
|
7-2
|
Nie istnieje
|
|
7-6
|
Nie istnieje
|
Sprawdziliśmy działanie algorytmu dla węzłów 2,6,7. Badana sieć jest przeznaczona głównie do badania algorytmu maksymalnego przepływu, dlatego nie udało nam się zaobserwować niczego interesującego. Większość połączeń da się realizować tylko w jedną stronę.
Analiza algorytmu maksymalnego przepływu.
Badana sieć ma bardzo ciekawe właściwości. Przykładowo, maksymalny przepływ między węzłami:
1 a 7 wynosi 60. Na ten przepływ składają się ścieżki:
1-2-5-7 (waga 20), 1-3-2-5-7 (waga 10), 1-3-4-7 (waga 20), 1-3-4-5-7 (waga 10).
Możemy zauważyć , że niektóre połączenie międzywęzłowe, są wykorzystywane, przez parę ścieżek. Przykładowo, połączenie 5-7 jest wykorzystywane przez 3 ścieżki (1-2-5-7, 1-3-5-7, 1-3-4-5-7)
3 a 7 wynosi 40. Składają się na niego ścieżki:
3-2-5-7 (waga 10), 3-4-7 (waga 20), 3-4-5-7 (waga 10).
Widać, że połączenie 5-7 zostało wykorzystane dwukrotnie.
- Własna sieć
Zgodnie z instrukcjami dotyczącymi ćwiczenia zaprojektowaliśmy własną sieć o 7 węzłach, 9 połączeniach jednostronnych i 4 połączeniach obustronnych. Zaprojektowaną sieć i macierz przedstawiają rysunki zamieszczone na kolejnej stronie.
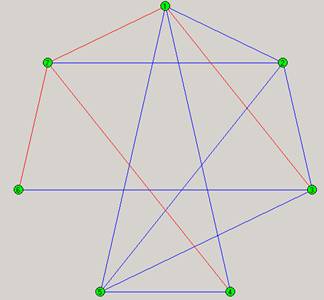
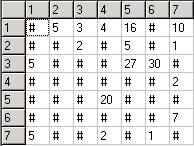
Analiza algorytmu najkrótszej drogi.
|
TRASA
|
DŁUGOŚĆ DROGI
|
|
1-2-5
|
10
|
|
1-4-7-6
|
7
|
|
5-4-7-1
|
27
|
|
5-4-7-6
|
23
|
|
6-7-1
|
12
|
|
6-7-1-2-5
|
22
|
Korzystając z algorytmu najkrótszej drogi, zbadaliśmy wzajemne długości drogi dla węzłów: 1,5,6. Ponownie możemy zaobserwować, że nie zawsze połączenie bezpośrednie, jak ma to miejsce w przypadku połączenia między węzłami 1 i 5, jest połączeniem najkrótszym. Analizując naszą sieć można łatwo zauważyć że drogi "powrotne" do węzła 1, mają większe wagi, przez co trasa wybierana jest z wykorzystaniem pozostałych węzłów, co w rezultacie daje nam mniejszą wagę, niż gdybyśmy chcieli dostać się bezpośrednio do węzła 1.
Analiza algorytmu maksymalnego przepływu.
Z pliku Dijkstra.net zbadaliśmy maksymalny przepływ w sieci między węzłami:
Od 3 do 7 - maksymalny przepływ wynosi 14. Na ten przepływ składają się ścieżki:
3-1-7 (waga 5), 3-6-7 (waga 7), 3-5-4-7 (waga 2). W naszej sieci mniejsze wagi przypisaliśmy pierwszym węzłom, natomiast większe wagi węzłom ostatnim. Udało nam się zatem zaobserwować że wszystkie pakiety, wysyłane w każdym możliwym kierunku, dzięki wysokim wagom węzłów końcowych docierały w całości, bez strat do węzła 7.
Od 2 do 6 - maksymalny przepływ wynosi 5. Na ten przepływ składają się ścieżki:
2-5-4-7-6 (waga 2), 2-3-1-7-6 (waga 1), 2-3-6 (waga 2). W tym przykładzie udało nam się zaobserwować, że ilość pakietów wysyłanych z jednego węzła maleje wraz z przechodzeniem przez dosyć skomplikowaną sieć. Jak widać duża liczba węzłów wcale nie musi zapewniać wysokiego przepływu, kilka niedoskonałych węzłów, może znacząco obciążyć całą sieć, doprowadzając do opóźnień. Tej sytuacji dałoby się uniknąć korzystając z mniejszej ilości, ale za to lepszej jakości, węzłów.
3. Wnioski końcowe
Podczas ćwiczenia zbadaliśmy dwa algorytmy: Dijkstry i Dinica. Pierwszy z nich jest algorytmem najkrótszej drogi (jest odpowiedzialny za wyznaczenie najkrótszej drogi pomiędzy węzłami sieci). Badaliśmy połączenia między węzłami sieci, którym przypisano, bądź sami przypisaliśmy określone długości połączenia. Długość połączenia jest określona wagą łuków, a rolę wagi pełnić może koszt drogi, jej długość bądź przepustowość.
Analizując otrzymane wyniki zauważyliśmy, że wyznaczona droga pomiędzy dwoma węzłami jest różna w zależności od kierunku uzyskiwania połączenia. Efekt ten jest szczególnie wyraźny, gdy wyznaczona droga wykorzystuje połączenia jednokierunkowe. W takim wypadku możliwe jest również, że próba nawiązania połączenia zakończy się niepowodzeniem. W przypadku wykorzystania łącza dwukierunkowego taka sytuacja nie ma miejsca. Wykorzystanie połączenia dwukierunkowego nie jest jednak gwarancją uzyskania trasy niezależnej od kierunku przepływu informacji. Droga ta ma być najkrótsza, co oznacza, że suma wag łuków budujących połączenie ma być najmniejszą z możliwych, a łącze dwukierunkowe może posiadać różne wagi, nawet większe od sumy wag z wykorzystaniem większej ilości węzłów.
Kolejny badany przez nas algorytm - Dinica - poszukuje wszelkie możliwe połączenia między dwoma węzłami, o możliwie największej przepustowości (z jednego węzła wysyłamy pakiety, w drugim je odbieramy). Rozmiar wysyłanych pakietów jest zależna od wagi między węzłami. Przykładowo, jeśli z węzła 3 do 4 możemy wysyłać 100 Mb/s a z węzła 4 do 5 1Mb/s, to w rzeczywistości przepustowość między węzłami 3 i 5 wynosi 1 Mb/s.
Algorytm poszukiwania maksymalnego przepływu jest dość złożony. Nie zawsze możemy wybrać jedną ścieżkę i w całości wykorzystać jej pojemność. Należy mieć na uwadze to, że poszczególne połączenia międzywęzłowe mogą być wykorzystywane przez parę ścieżek naraz, tak więc wykorzystując w pełni pojemność danej ścieżki, blokujemy inne połączenia. Przy projektowaniu sieci, należy mieć również na uwadze to, że duża ilość węzłów powoduje nie potrzebne opóźnienia. Możemy wybrać ścieżkę składającą się z 10 węzłów o przepustowości 20, albo też ścieżkę składającą się z dwóch węzłów o przepustowości 15. Należy mieć na uwadze opóźnienia na węzłach.
Podsumowując, przeprowadzone ćwiczenie uważam za wykonane poprawnie. Dało ono satysfakcjonujące rezultaty, potwierdzające teoretyczne założenia badanych algorytmów.


