Wg definicji bryła sztywna to układ punktów materialnych, które zajmują zawsze te same położenia względem siebie. Tak więc w ruchu postępowym takiego ciała, wszystkie punkty materialne będą poruszać się z taką samą prędkością liniową, a jeśli będzie to ruch jednostajnie zmienny to będą miały takie same przyspieszenie.

Jeżeli połączy się jakiekolwiek dwa punkty ciała sztywnego to okaże się, że odcinek, który je łączy biegnie równolegle do odcinka łączącego te same dwa punkty, ale w poprzednim położeniu.

Można również rozważać ruch obrotowy ciała sztywnego. Szczególny przypadek stanowi sytuacja, gdy oś obrotu jest nieruchoma. Każdy punkt takiego ciała, o masie m za wyjątkiem tych leżących na osi obrotu, będzie poruszał się po okręgu o promieniu r, równym odległości tego punktu od osi obrotu. Jego prędkość kątowa 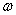 będzie wynosiła : 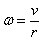, gdzie v to prędkość liniowa. Zatem jego energię kinetyczną można obliczyć z zależności: 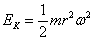. Całkowita energia kinetyczna bryły sztywnej w tym ruchu jest równa sumie energii kinetycznych poszczególnych punktów materialnych.

Z definicji bryły sztywnej wynika, że w tym ruchu wszystkie punkty będą miały taka samą prędkość kątową 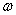. Tak więc całkowitą energię kinetyczną bryły można przedstawić w postaci wzoru:

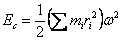
W tym wzorze iloczyny miripochodzą od poszczególnych punktów materialnych bryły.

Sumę tych iloczynów nazywa się momentem bezwładności I bryły sztywnej względem osi obrotu.

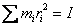
Moment bezwładności zależy nie tylko od osi obrotu, ale także od kształtu bryły i rozkładu gęstości. Wyraża się go zwykle w .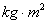

I tak w zależności od kształtu bryły sztywnej wzór na moment bezwładności może przyjmować różną postać. Np. dla kuli wynosi: 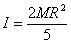, gdzie M- masa kuli, R - jej promień,

Dla cienkiego pręta natomiast moment bezwładności względem osi przechodzącej przez jeden z jego końców wyraża się zależnością: 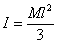, gdzie l to długość pręta.

Jeżeli bryła sztywna wykonuje ruch obrotowy z przyspieszeniem kątowym, to dzieje się tak pod wpływem przyłożonej siły. Jeżeli siła F działa na punkt materialny bryły sztywnej to jej działanie automatycznie przenosi się na całą bryłę. Mówi się nie o samej sile, ale o tzw. momencie siły. Można go obliczyć ze wzoru:

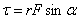
gdzie r to odległość punktu przyłożenia siły od osi obrotu, a kąt alfa zawarty jest między prostą łączącą punkt przyłożenia siły z osią obrotu i wektorem siły F.

Podobnie jak w ruchu postępowym, w ruchu obrotowym również obowiązują zasady dynamiki.

Pierwsza zasada dotyczy sytuacji kiedy bryła sztywna nie porusza się lub ma stałą prędkość kątową. Wtedy to wypadkowy moment sił względem danej osi obrotu, działających na ciało jest równy zero.

Wg drugiej zasady jeśli bryła sztywna poddana jest działaniu stałego momentu sił to porusza się ona z przyspieszeniem kątowym wprost proporcjonalnym do tego momentu sił co do wartości i odwrotni proporcjonalnym do momentu bezwładności.