Pędem punku materialnego nazywa się iloczyn masy tego ciała i jego prędkości. W rzeczywistości pęd jest wielkością wektorową, podobni jak i prędkość. Można więc zapisać:
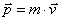
Na podstawie tego równani widać, że pomiędzy pędem a prędkością danego punku materialnego zachodzi proporcjonalność.
Sformułowanie drugiej zasady dynamiki Newtona z użyciem pojęcia pędu mówi, że zmiana pędu danego ciała zachodząca w określonej jednostce czasu jest proporcjonalna do wypadkowej siły która działa na to ciało. Kierunek wektora pędu jest taki sam jak kierunek wektora siły.
Zgodnie więc z tym stwierdzeniem można druga zasadę dynamiki zapisać jako:
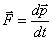
Jeżeli więc mamy do czynienia z punktem materialnym i możemy w takiej sytuacji założyć stałość masy wówczas z powyższej zależności przechodzi się do tradycyjnego zapisu drugiej zasady dynamiki czyli:
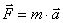
Tak więc widać , że dla punktów materialnych można zamiennie korzystać z tych dwóch równań.
Według teorii względności poprawny jest jednak zapis drugi. Jest jednak jeden warunek, pęd musi być przedstawiony jako:
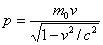
gdzie : v - prędkość punktu materialnego, c - prędkość światła w próżni a m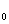 to masa spoczynkowa tego punktu.
to masa spoczynkowa tego punktu.
Zamiast pojedynczego punktu materialnego może wystąpić cały układ takich punktów. W takiej sytuacji przy założeniu, że masa układu jest stała całkowity pęd będzie geometryczną sumą pędów poszczególnych punktów materialnych. Po ich zsumowaniu dostajemy zależność:
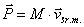
gdzie M to całkowita masa układu , a v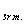 to prędkość środka masy.
to prędkość środka masy.
Można więc powiedzieć, że całkowity pęd układu punktów materialnych równa się iloczynowi całkowitej masy tego układu i prędkości środka masy tego układu.
Druga zasada dynamiki Newtona dla układu punktów materialnych będzie przyjmowała postać:
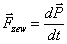
Gdzie F to suma geometryczna wszystkich sił zewnętrznych , które działają na dany układ punktów materialnych.
Jedną z podstawowych zasad fizyki jest zasada zachowania pędu. Mówi ona, że jeśli wypadkowa siła zewnętrzna działająca na układ jest równa zero to całkowity pęd układu nie ulega zmianie. W obrębie układu pojedyncze pędy mogą się zmieniać, ale suma tych pędów musi pozostać stała.
Na całkowity pęd układu wpływ mają tylko siły zewnętrzne i to one mogą dokonać jego zmiany.
Zasadę zachowania pędu można także stosować, jeśli mamy do czynienia ze zderzeniem dwóch ciał pod warunkiem ,że czas zderzenia jest dostatecznie krótki. No i oczywiście o ile nie występują siły zewnętrzne.
Można rozważyć zatem układ składający się z dwóch cząstek. Pomiędzy tymi cząstkami dochodzi do zderzenia. W momencie zderzenia między tymi cząstkami działają wewnętrzne siły impulsowe. Można zatem zapisać, że zmiana pędu pierwszej cząstki jest równa:
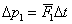
gdzie F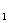 to średnia siła , z jaką cząstka pierwsza działa na cząstkę drugą w trakcie zderzenia. I analogicznie dla drugiej cząstki można zapisać:
to średnia siła , z jaką cząstka pierwsza działa na cząstkę drugą w trakcie zderzenia. I analogicznie dla drugiej cząstki można zapisać:
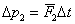
gdzie F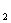 to średnia wartość siły działania cząstki drugiej na cząstkę pierwszą.
to średnia wartość siły działania cząstki drugiej na cząstkę pierwszą.
Całkowita zmiana pędu układu pod warunkiem, że na układ nie działają żadne inne siły jest sumą zmian pędów obu cząstek. Można zatem zapisać :
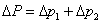
Wiadomo jednak, że obie siły, F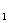 i F
i F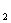 są takie same co do wartości lecz przeciwnie skierowane. Można zatem zapisać, że :
są takie same co do wartości lecz przeciwnie skierowane. Można zatem zapisać, że :
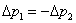
A więc całkowita zmiana pędu tego układu będzie równa:
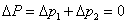
Widać więc , że całkowity pęd układu jest zachowany.
Można także przeanalizować inny przykład. Mamy teraz dwa ciała o masach m1 i m2. Ciała te zostały połączone sprężyną. Znajdują się w spoczynku na idealnie gładkiej powierzchni. I teraz jak będzie wyglądał pęd całego układu jeśli najpierw oba ciała zostaną rozsunięte, a następnie puszczone swobodnie. W momencie gdy ciała zostają puszczone na układ nie działa już żadna siła zewnętrzna. Obowiązuj więc zasada zachowania pędu. Zanim ciała zostały uwolnione pęd układu był równy zero. Będzie więc równy zero także po ich uwolnieniu. Wynika to właśnie z zasady zachowania pędu.


