ZJAWISKA RUCHU CZĄSTECZEK - ANALIZA

Teraz zajmijmy się dopełnieniem tych dyskusji teoretycznych, wzorcową analizą ilościową - z potrzeby fragmentaryczną - zjawiska ruchu cząsteczek.

Zad 1.

Wyliczyć średnią prędkość kwadratową cząsteczek dwutlenku węgla (CO₂) w przeciętnych warunkach, czyli w temperaturze 0^oC pod ciśnieniem 1 atm. Zakładamy, że gaz jest gazem doskonałym .

Do przeprowadzenia obliczeń korzystnie jest nam posługiwać się terminem średniej energii kinetycznej cząsteczek branego pod uwagę gazu (CO₂).

Ciśnienie (p) definiowane jest za pomocą wzoru:

p = 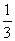 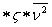(1)

gdzie:

- V - gęstość gazu, inaczej mówiąc masa przypadającą na jednostkę objętości;

- n - średnia wartość prędkości cząsteczek gazu.

Nie zagłębiając się w analizę powyższego wzoru zauważyć można, że ciśnienie (p) jest wprost proporcjonalne do średniej energii kinetycznej cząsteczek (E _{k. ś.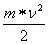} = ), emitowanej np. ściankom pojemnika mając na uwadze, że V = ^masa / _objętość).

Należy również zwrócić uwagę, że dla wszystkich cząsteczek

v² = v_x² + v_y² + v_z²

gdzie:

- v_x, v_y, v_z - składowe wektora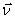

Jako, że mamy dużą liczbę cząsteczek przemieszczających się chaotycznie. Żaden z kierunków (v_x, v_y, v_z) nie jest specjalnie podkreślony, zatem zgodne jest założenie, iż jest średnie wartości v_x, v_y, v_z są sobie równe. Możemy więc zapisać to w następujący sposób:

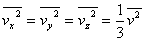
Otrzymaliśmy odpowiedz skąd się bierze współczynnik 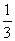 we wzorze (1).

W oparciu o wzór (1) określono prędkość średnią kwadratową cząsteczek, która jest miarą umiarkowanej prędkości cząsteczek:

v _{ś. kw.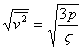} =  (2)

Zatem gdy chcemy wyliczyć zadaną w zadaniu 1 wielkość musimy znaleźć tylko gęstość dwutlenku węgla - V (ciśnienie (p) mamy podane), a później wstawić p i V do wzoru (2).

W naturalnych warunkach 1 mol (gramocząsteczka) gazu, czyli 6,022*10²³ (liczba Avogadro - N_A) cząsteczek, zajmuje objętość równą 22,4 dm³. Masa molowa (m) gazu jest wielkością masy przypadającej na 1 mol tego gazu ( m = m _cz.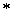 N_A )

Cząsteczka dwutlenku węgla zbudowana jest z atomu węgla i dwóch atomów tlenu. Masy atomowe szukanych przez nas pierwiastków odszukujemy w tablicy Mendelejewa. Bierzemy pod uwagę wartości zaokrąglone:

- węgiel (C) - 12

- tlen (O) - 16

Podstawiając do wzoru odczytane wartości uzyskujemy masę dwutlenku węgla:

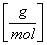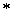m CO₂ = 44  = 44  10^-3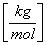

Teraz jesteśmy w stanie wyliczyć gęstość CO₂

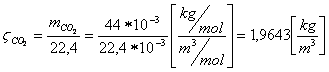
Otrzymany wynik podstawiamy do wzoru (2), przyjmujemy, że p wynosi p=1,013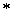10⁵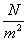

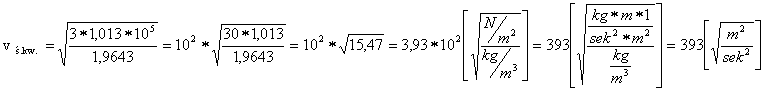
Zatem uzyskaliśmy wynik:

v _{ś. kw.} = 393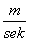

Można zauważyć, że jest to ogromna prędkość.

Zad 2.

Wyliczyć długość średniej drogi swobodnej metalicznych kuli, będących w żwawo potrząsanej "grzechotce" w postaci kuli o średnicy 10 cm. Należy przyjąć średnicę wszystkich z 15 kul d = 1 cm.

Jak zauważamy spotykamy się tu z "modelem" cząsteczki gazu, która wprawiana jest w ruch ruchem chaotycznym w danej objętości.

Wiemy, że długość średniej drogi swobodnej cząsteczki, czyli na takiej drodze, gdzie nie ma mowy o do zderzeniu z inną cząsteczką, zapisujemy za pomocą następującego wzoru:

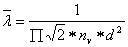 (3)

gdzie:

- n_v - ilość cząsteczek przypadająca na jednostkę objętości;

- d - średnica każdej z cząsteczek.

Dzięki temu modelowi uzyskamy(jednak w znacznym przybliżeniu) nieruchomy ruch kuli ("cząsteczek") we wszystkich możliwych kierunkach. (Jak da się zauważyć 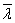 we wzorze (3) nie zależy od prędkości cząstek) W naszym "modelu" przyjmujemy także, iż kule (inaczej"cząsteczki") są umieszczone w próżni. W związku z tym, że duża wielokrotność masy kulki porównując z masą cząsteczek powietrza oddziaływanie zderzeń kulek z cząsteczkami powietrza da się ostatecznie zaniedbać.

Obliczyć musimy jeszcze "gęstość" zbioru 15 kulek -czyli obliczyć liczbę kulek, przypadającą na jednostkę objętości.

n_v =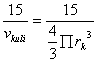  

gdzie:

- r_k = 5 cm.

Otrzymany wynik wstawiamy do wzoru (3):

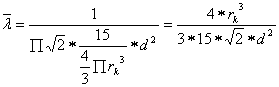
gdzie:

- r_k = 5 cm

- d = 1 cm

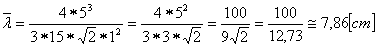
Zatem średnia droga, na której kulka nie zderza się z inną kulką równa jest niemal 8 cm. Da się zauważyć, iż najdłuższy odcinek prosty, który jest w stanie przemieścić się w "grzechotce" da w wyniku nieco więcej i równy jest średnicy kuli (10 cm). Gdyby było 10 kulek, wtedy:

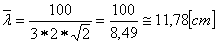
Zatem jest większa niż średnica kulki( wydaje się nam to niemożliwe), ponieważ kula nie może przebyć tak długiej drogi swobodnej; wcześniej nastąpi zderzenie ze ścianką.

Wytłumaczmy teraz tą sytuację. Ustanowiony przez nas model nie sprawdza się wszędzie . Ma on sens tylko w warunkach rzeczywistych gazów, gdzie n_v (patrz wzór (3)) jest bardzo wielki. Dostrzec możemy również , że przy takiej samej gęstości kul n_v, w naszym przypadku wystarczy 100 razy powiększyć objętość "grzechotki" i 100 razy ilość kul i wtedy uzyskamy taką samą długość 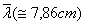. Wielkość ta będzie mieć sens, tylko wtedy gdy najdłuższy odcinek prosty, będący w zwiększonej kuli (jej średnicy) wzrośnie kilka razy.

W laboratoriach są także takie sytuacje, gdzie długość średniej drogi swobodnej w bardzo ograniczonej przestrzeni (np. synchrotron protonowy) stać się może kolosalną wielokrotnością rozmiarów tej ograniczonej przestrzeni. ( na przykład w synchrotronie protonowym sięga ona rzędu miliona kilometrów). Dostaje się takie wyniki przy użyciu pola magnetycznego, który nadaje protonom (przemieszczającym się w próżni), ruch po torze kołowym. W związku z tym protony nie zderzają się z obudową.