1. Ilość ciepła przetransportowana przez dwie izotermiczne, równoległe powierzchni w kierunku do nich prostopadłym,

określająca na jednostkę powierzchni oraz jednostkę czasu przedstawia się wzorem Fouriera

gdzie :

współczynnik proporcjonalności K nazywa się współczynnikiem przewodnictwa cieplnego. Kierunek przepływu strumienia cieplnego q jest przeciwny do gradientu temperatury 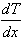o czym informuje nas znak minus w równaniu.

2. Ilość ciepłą przetransportowana przez powierzchnię S w czasie τ ,

w przypadku, gdy odległość pomiędzy powierzchniami wynos id, natomiast różnica temperatur pomiędzy nimi ΔT, wynosi

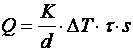
Strumień cieplny q wówczas wynosi

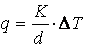
3. Siła tarcia pomiędzy dwoma warstwami gazu, które przemieszczają się równolegle z różnymi prędkościami względem siebie, wyraża się wzorem

gdzie:

S - pole powierzchni przylegających warstw

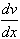- gradient prędkości ruchu warstw w kierunku x prostopadłym do powierzchni

η - współczynnik tarcia wewnętrznego (lepkość dynamiczna)

4. Cecha przepływu cieczy (gazu) wyraża się z wartości liczby Reynoldsa

l - podany rozmiar przekroju poprzecznego kanału albo opływanego ciała,

v - prędkość przepływu,

ν - współczynnik lepkości kinematycznej, który równy jest stosunkowi współczynnika dynamicznego lepkości η do gęstości cieczy (gazu) ρ. Dla niewielkich Re (tan. dla niewielkich wartości v oraz l) przepływ ma charakter laminarny oraz opór ośrodka uzależniony jest od sił tarcia. Zgodnie z wzorem Stokesa siła oporu w tym wypadku wynosi

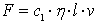
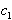- współczynnik proporcjonalności zależy od formy ciała.

Dla kuli o małym promieniu r współczynnik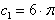

wówczas wzór Stokesa wynosi

Dla ogromnych Re przepływ cieczy (gazu) jest turbulentny natomiast opór ruchu wynosi

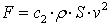
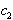- współczynnik proporcjonalności uzależniony jest od formy ciała,

S - przekrój poprzeczny ciała.

5. Masa gazu przetransformowana w czasie t przez powierzchnię S w kierunku x, prostopadłym do tej powierzchni

D - współczynnik dyfuzji,

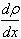- gradient gęstości