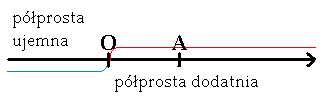
Osią liczbową nazywamy taką prostą, na której:
- Został obrany pewien punkt O zwany punktem zerowym lub początkiem osi liczbowej,
- Jedna z półprostych o początku w punkcie O została nazwana półprostą dodanią,
- Został obrany taki punkt A na półprostej dodatniej, że długość odcinka
![00029072.png]() równa jest 1.
równa jest 1.
Podzbiory liczb rzeczywistych nazywamy przedziałami.
Niech a i b będą takimi liczbami rzeczywistymi, że a
Przedziałem otwartym o końcach a i b nazywamy zbiór wszystkich takich liczb rzeczywistych x, że a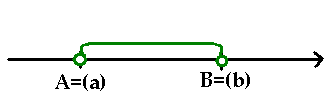
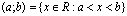
Przedziałem domkniętym o końcach a i b nazywamy zbiór liczb rzeczywistych x spełniających nierówność . Przedział ten oznaczamy przez 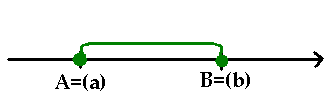
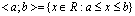

- Podobnie określamy przedział prawostronnie domknięty (a;b> o końcach a i b.
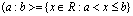

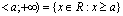
- Podobnie określa się przedziały otwarty i domknięty nieograniczone z lewej strony o końcu a, które oznaczamy odpowiednio
![00029089.png]() i
i ![00029089.png]() .
. - Rozważa się też często przedział nieograniczony z obu stron
![00029091.png]() . Jest to po prostu zbiór wszystkich liczb rzeczywistych.
. Jest to po prostu zbiór wszystkich liczb rzeczywistych.

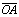 równa jest 1.
równa jest 1.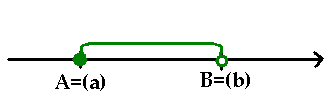


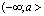 i
i 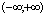 . Jest to po prostu zbiór wszystkich liczb rzeczywistych.
. Jest to po prostu zbiór wszystkich liczb rzeczywistych.
