1 - Równania Maxwella
Są to podstawowe równania opisujące zachowanie się pól elektromagnetycznych, stanowią unifikację teorii pola elektrycznego i magnetycznego. Równań tych jest cztery i wśród nich wyróżniamy równania: Gaussa, Ampera, indukcji Faradaya. Prawa te można przedstawić w postaci całkowej:
- Prawo Gaussa:
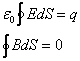
- Prawo Ampera:
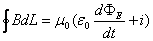
- Prawo indukcji Faradaya
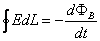
Równania Maxwella w postaci różniczkowej:
-
![]() - jest to różniczkowa postać prawa Gaussa, które to mówi, że ładunek elektryczny wytwarza pole elektryczne wokół siebie, a które maleje wraz z kwadratem odległości od ładunku.
- jest to różniczkowa postać prawa Gaussa, które to mówi, że ładunek elektryczny wytwarza pole elektryczne wokół siebie, a które maleje wraz z kwadratem odległości od ładunku. -
![]() - równanie to nie ma jakieś szczególnej nazwy, jednak opisuje bardzo ważną własność przyrody, otóż nie występują pojedyncze ładunki magnetyczne.
- równanie to nie ma jakieś szczególnej nazwy, jednak opisuje bardzo ważną własność przyrody, otóż nie występują pojedyncze ładunki magnetyczne. -
![]() - jest to różniczkowa postać prawa indukcji Faradaya, które głosi, że zmienne pole magnetyczne powoduje powstanie zmiennego pola elektrycznego, co z kolei może prowadzić do przepływu prądu elektrycznego.
- jest to różniczkowa postać prawa indukcji Faradaya, które głosi, że zmienne pole magnetyczne powoduje powstanie zmiennego pola elektrycznego, co z kolei może prowadzić do przepływu prądu elektrycznego. -
![]() - jest to różniczkowa postać prawa Ampera, które głosi, że istnienie zmiennego pola elektrycznego, lub przepływ prądu elektrycznego, powoduje powstanie wirowego pola magnetycznego.
- jest to różniczkowa postać prawa Ampera, które głosi, że istnienie zmiennego pola elektrycznego, lub przepływ prądu elektrycznego, powoduje powstanie wirowego pola magnetycznego.
Równania Maxwella w postaci całkowej:
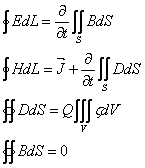
2 - Laser (na przykładzie lasera rubinowego)
Rubin jest specyficznym kryształem Glinu, bowiem część atomów Al, została zamieniona na atomu Chromu - Cr.
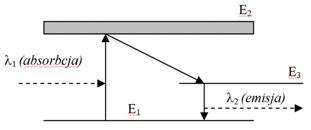
Na powyższym rysunku przedstawiono schemat poziomów energetycznych. Są to poziomy energetyczne ośrodka czynnego, który stanowi główną część lasera. W przypadku lasera rubinowego, ośrodkiem czynnym jest rubin. Przez ośrodek czynny przepuszczane jest promieniowanie o długości fali l1. Promieniowanie to jest absorbowane przez atomy chromu, wskutek czego przechodzą one do stanu wyższego energetycznie - stanu E2. W ten sposób powstaje pasmo energetyczne, o pewnej szerokości. Poziom ten jest niestabilny i po pewnym czasie (czasie życia poziomu energetycznego), atomy chromu przechodzą do stanu metastabilnego - stanu E3, który to charakteryzuje się znacznie dłuższym czasem życia niż E2. W wyniku takiego zabiegu, duża liczba atomów chromu przechodzi do stanu E3. Dostajemy w ten sposób tak zwaną inwersję obsadzeń, gdyż większa ilość atomów znajduje się w stanie wzbudzonym (E3), niż w stanie podstawowym (E1) - N3>N1. Gdy atom po pewnym czasie przejdzie do poziomu podstawowego E1, nastąpi emisja promieniowania o ściśle określonej długości fali -  , którego fotony poruszające się równolegle do osi lasera, będą odbijane od zwierciadeł znajdujących się na jego końcach, w wyniku czego narastać będzie proces emisji wymuszonej promieniowania.
, którego fotony poruszające się równolegle do osi lasera, będą odbijane od zwierciadeł znajdujących się na jego końcach, w wyniku czego narastać będzie proces emisji wymuszonej promieniowania.
3 - Równanie fali kulistej
Wyprowadzenie:
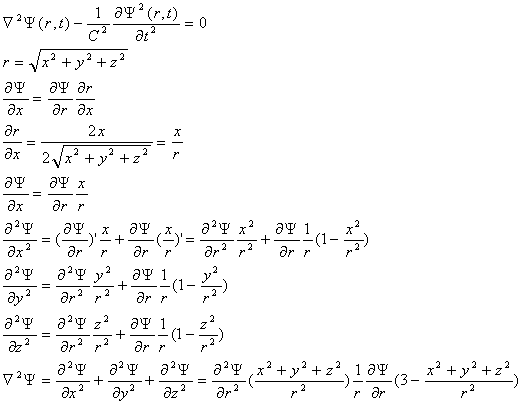
Ostateczna postać równania fali kulistej:
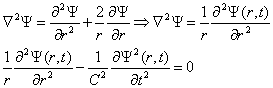
4 - Dyfrakcja - siatka dyfrakcyjna
Zakładamy, że mamy dwie takie same szczeliny, tak jak to pokazano na rysunku poniżej:
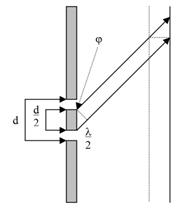
Związki pomiędzy kątem φ, odległością d i długością fali λ, przedstawiają się w następujący sposób:
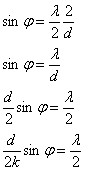
Możemy teraz określić warunki na wzmocnienie i wygaszenie fali, na wskutek interferencji ze sobą:
Wzmocnienie fali gdy - 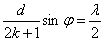
Wygaszenie fali gdy - 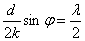
Funkcja opisująca rozkład natężenia światła po przejściu przez układ szczelin:
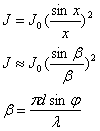
gdzie J0, oznacza pierwotne natężenie światła.
5 - Emisja termoelektronowa
Pod wpływem ogrzania ciała do bardzo wysokiej temperatury, może wystąpić zjawisko emisji elektronów przez to ciało, czyli do tzw. emisji termoelektronowej. Dzieje się tak, gdyż dostarczane ciepło do układu, zamieniane jest na energię kinetyczną elektronów, która może wzrosnąć do takiej wartość przy której elektron może wyrwać się z atomu i stać się elektronem swobodnym i dodatkowo opuścić dane ciało.
Proces ten można opisać stosując statystykę Maxwella - Boltzmana:

Czynnik  to tak zwana stała Richardsona - A.
to tak zwana stała Richardsona - A.
Dzięki czemu otrzymujemy wzór na termoemisję:
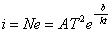
gdzie b oznacza minimalną wartość energii, jaką należy dostarczyć elektronowi, aby stał się elektronem swobodnym - tzw. praca wyjścia.
6 - Prąd elektryczny, natężenie i gęstość.
Jeśli mamy przewodnik o przekroju poprzecznym ΔS, przez który przepływają ładunki o koncentracji n0 [ładunek/cm3] z prędkością V, to całkowity ładunek jaki przepłynie w jednostce czasu Δt wynosi:
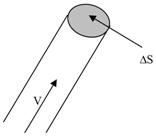
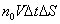
Całkowity ładunek jaki przepłynie przez taki przewodnik:
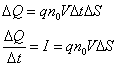
Gdzie I oznacza natężenie prądu elektrycznego.
Do tego momentu zakładaliśmy, że wszystkie ładunki poruszają się z taką samą prędkością. W przypadku jednak, kiedy prędkości ładunków nie są takie same, ruch ładunków można porównać do ruchu cząsteczek gazu, w związku z czym prędkość V należy zastąpić prędkością średnią:
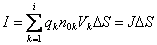
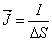
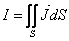
gdzie J oznacza gęstość prądu elektrycznego.
7 - Cząstka w studni potencjału
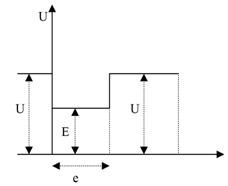
U - energia potencjalna cząstki
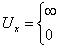
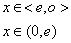
Rozwiązanie równania Schrodingera dla obszaru I, dla studni Ux:
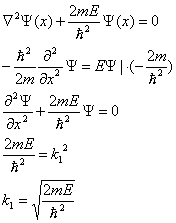
Równanie fali:
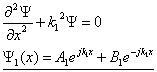
Rozwiązanie równania Schrodingera dla obszaru II i III:

Z warunku ciągłości funkcji falowej:
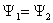
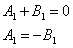
Ostatecznie równanie fali:

8 - Cząstka i bariera potencjałów
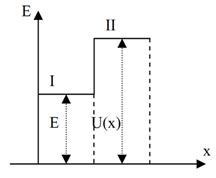
E - energia
Rozpatrujemy I obszar:
- cząstka posiada tylko energię kinetyczną
Równanie Schrodingera w tym obszarze:

Rozpatrujemy II obszar:

Na granicy pomiędzy obszarami I i II może dojść do odbicia cząstki. Może także dojść do przejścia cząstki przez tą granicę, jednak gdy już znajdzie się w obszarze II to w nim nie może dojść do odbicia, bowiem B2=0.
Definiujemy współczynnik odbicia R i przejścia D, takie, że R + D = 1:
Współczynnik odbicia - 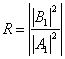
Współczynnik przejścia - 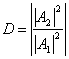
9 - Potencjał wektorowy
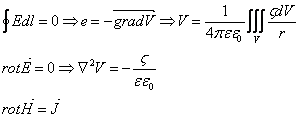
Przy czym:
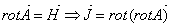
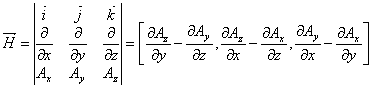
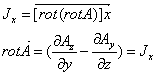

10 - Oscylator harmoniczny tłumiony
Korzystając z II zasady dynamiki Newtona, równanie ruchu oscylatora harmonicznego tłumionego można rozpisać w następujący sposób:
FS - siła sprężystości
Ft - siła tłumienia (oporu)
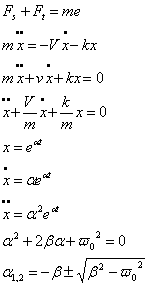
W zależności od wielkości parametru ω0, można wyróżnić 3 charakterystyczne przypadki:
1 - 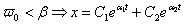
2 - 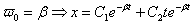
3 - 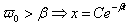
We wszystkich tych przypadkach obserwujemy zmniejszanie się amplitudy drgań wraz z upływem czasu.
Logarytmiczny dekrement tłumienia (wielkość charakterystyczna dla drgań tłumionych):
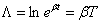
11 - Efektywna masa elektronu
Jest to wielkość różniąca się od masy rzeczywistej elektronu, ale uwzględniająca energię elektronu i wartość prądu elektrycznego:
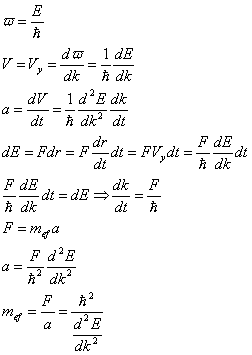
W przypadku cząstki swobodnej, jej masa efektywna jest równa jej masie rzeczywistej:
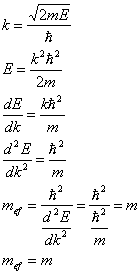
12 - Ciało doskonale czarne, jego promieniowanie
Ciało charakteryzujące się określoną temperaturą emituje promieniowanie elektromagnetyczne o określonej energii:
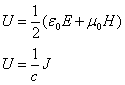
Energia zaabsorbowana - 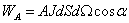
Energia wyemitowana - 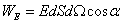
Prawo Kirchoffa - 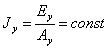 , gdzie Ey - zdolność emisji, Ay - zdolność absorpcji
, gdzie Ey - zdolność emisji, Ay - zdolność absorpcji
Prawo Stefana - Boltzmana -  - gdzie ET - całkowita zdolność emisji ciała doskonale czarnego, T - jego temperatura bezwzględna.
- gdzie ET - całkowita zdolność emisji ciała doskonale czarnego, T - jego temperatura bezwzględna.
14 - Rozkład Fermiego - Diraca
Każde ciało posiada dwa pasma energetyczne: pasmo walencyjne i pasmo przewodnictwa. Gdy ciało znajduje się w bardzo niskiej temperaturze (bliskiej 0 K), wszystkie elektrony znajdują się w paśmie walencyjnym, a natomiast pasmo przewodnictwa jest puste. W miarę wzrostu temperatury, zwiększa się energia elektronów, które to mogą stopniowo przechodzić do pasma przewodnictwa, powodując w ten sposób powstawanie dziur w paśmie walencyjnym. W przypadku ciała, które to jest samoistnym półprzewodnikiem, liczba dziur w paśmie walencyjnym, równa jest liczbie elektronów w paśmie przewodnictwa. Zarówno liczba dziur jak i liczba elektronów rosną wraz ze wzrostem temperatury.
Energie elektronów charakteryzuje rozkład Fermiego - Diraca:
 , gdzie Ef oznacza energię na poziomie Fermiego (dla T = 0K).
, gdzie Ef oznacza energię na poziomie Fermiego (dla T = 0K).
Analiza rozkładu Fermiego - Diraca:
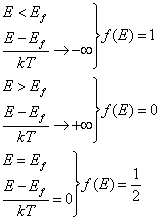
Wynik ostatniego przypadku, jest niezależny od temperatury.

 - jest to różniczkowa postać prawa Gaussa, które to mówi, że ładunek elektryczny wytwarza pole elektryczne wokół siebie, a które maleje wraz z kwadratem odległości od ładunku.
- jest to różniczkowa postać prawa Gaussa, które to mówi, że ładunek elektryczny wytwarza pole elektryczne wokół siebie, a które maleje wraz z kwadratem odległości od ładunku.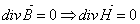 - równanie to nie ma jakieś szczególnej nazwy, jednak opisuje bardzo ważną własność przyrody, otóż nie występują pojedyncze ładunki magnetyczne.
- równanie to nie ma jakieś szczególnej nazwy, jednak opisuje bardzo ważną własność przyrody, otóż nie występują pojedyncze ładunki magnetyczne. - jest to różniczkowa postać prawa indukcji Faradaya, które głosi, że zmienne pole magnetyczne powoduje powstanie zmiennego pola elektrycznego, co z kolei może prowadzić do przepływu prądu elektrycznego.
- jest to różniczkowa postać prawa indukcji Faradaya, które głosi, że zmienne pole magnetyczne powoduje powstanie zmiennego pola elektrycznego, co z kolei może prowadzić do przepływu prądu elektrycznego.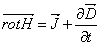 - jest to różniczkowa postać prawa Ampera, które głosi, że istnienie zmiennego pola elektrycznego, lub przepływ prądu elektrycznego, powoduje powstanie wirowego pola magnetycznego.
- jest to różniczkowa postać prawa Ampera, które głosi, że istnienie zmiennego pola elektrycznego, lub przepływ prądu elektrycznego, powoduje powstanie wirowego pola magnetycznego.
